pynamical

Python package for modeling, simulating, visualizing, and animating discrete nonlinear dynamical systems and chaos

Pynamical uses pandas, numpy, and numba for fast simulation, and matplotlib for visualizations and animations to explore system behavior.

Pynamical comes packaged with the logistic map, the Singer map, and the cubic map predefined. The models may be run with a range of parameter values over a set of time steps, and the resulting numerical output is returned as a pandas DataFrame. Pynamical can then visualize this output in various ways, including with bifurcation diagrams, two-dimensional phase diagrams, three-dimensional phase diagrams, and cobweb plots.

Citation info: Boeing, G. 2016. "Visual Analysis of Nonlinear Dynamical Systems: Chaos, Fractals, Self-Similarity and the Limits of Prediction." Systems, 4 (4), 37. doi:10.3390/systems4040037.

Install:

You can install pynamical with conda:

conda config --prepend channels conda-forge
conda create -n pynamical --strict-channel-priority jupyterlab pynamical

Alternatively, you can run pynamical + Jupyter directly from its Docker container, or you can install it with pip.

Documentation:

Available on readthedocs.

Demos/tutorial:

1. Pynamical: quick overview
2. Pynamical: the logistic model and bifurcation diagrams
3. Pynamical: 2D and 3D phase diagrams
4. Pynamical: static and animated cobweb plots
5. Pynamical: animated 3D phase diagrams
6. Pynamical: demonstrating other models

Quick walkthrough:

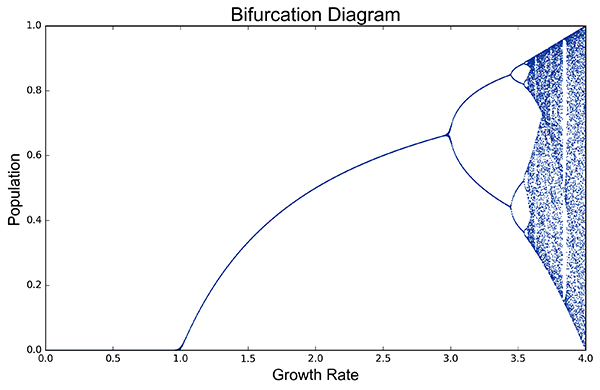
First load pynamical. Then simulate some model and visualize its bifurcation diagram in just 2 lines of code:

from pynamical import logistic_map, simulate, bifurcation_plot
pops = simulate(model=logistic_map, num_gens=100, rate_min=0, rate_max=4, num_rates=1000, num_discard=100)
bifurcation_plot(pops)

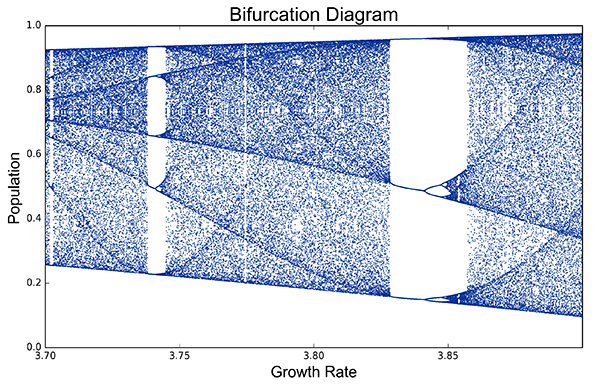
Zoom into a slice of this bifurcation diagram to see its fractal structure:

pops = simulate(model=logistic_map, num_gens=100, rate_min=3.7, rate_max=3.9, num_rates=1000, num_discard=100)
bifurcation_plot(pops, xmin=3.7, xmax=3.9)

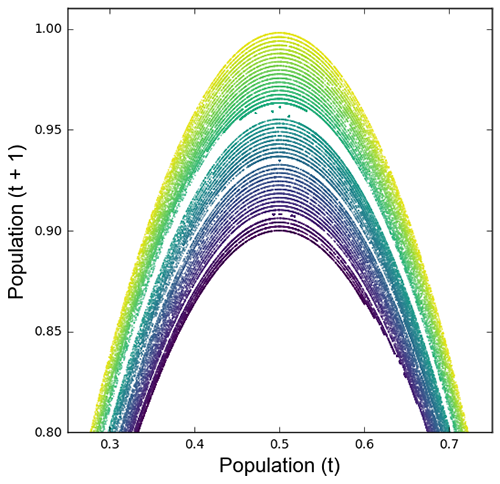
Plot a two-dimensional phase diagram of the logistic map:

from pynamical import phase_diagram
pops = simulate(model=logistic_map, num_gens=4000, rate_min=3.6, rate_max=4.0, num_rates=50, num_discard=100)
phase_diagram(pops, xmin=0.25, xmax=0.75, ymin=0.8, ymax=1.01, size=7, color='viridis')

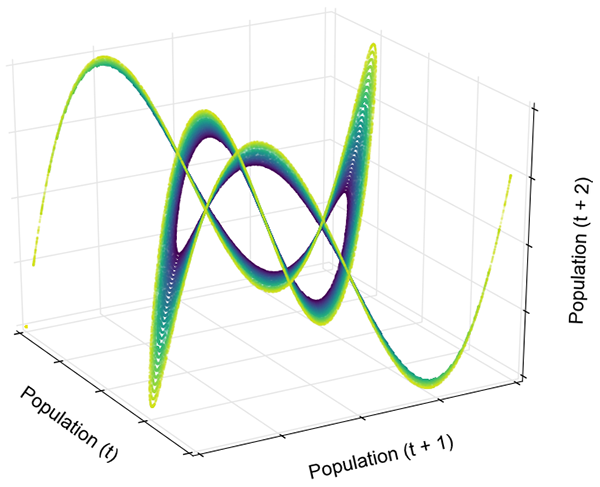
Or a three-dimensional phase diagram of the cubic map:

from pynamical import cubic_map, phase_diagram_3d
pops = simulate(model=cubic_map, num_gens=3000, rate_min=3.5, num_rates=30, num_discard=100)
phase_diagram_3d(pops, xmin=-1, xmax=1, ymin=-1, ymax=1, zmin=-1, zmax=1, alpha=0.2, color='viridis', azim=330)

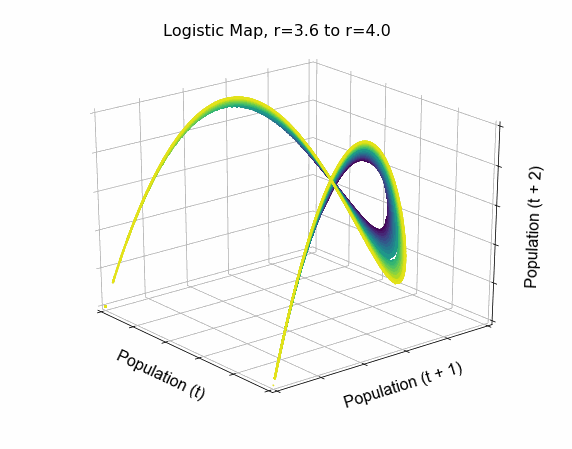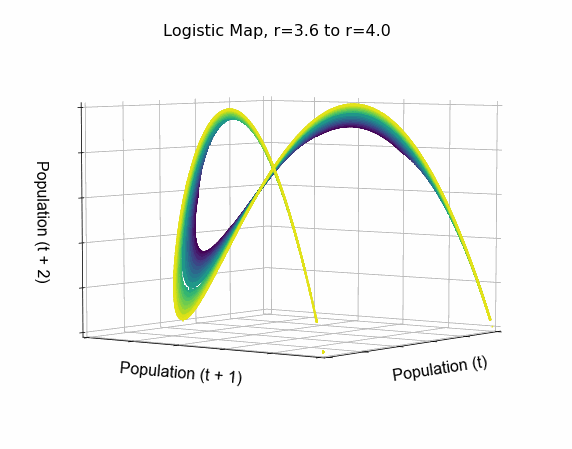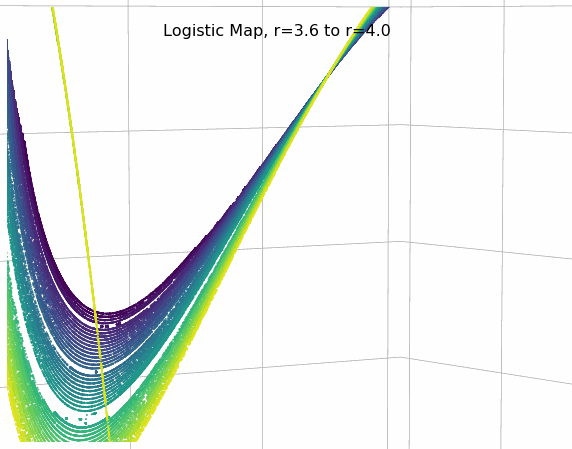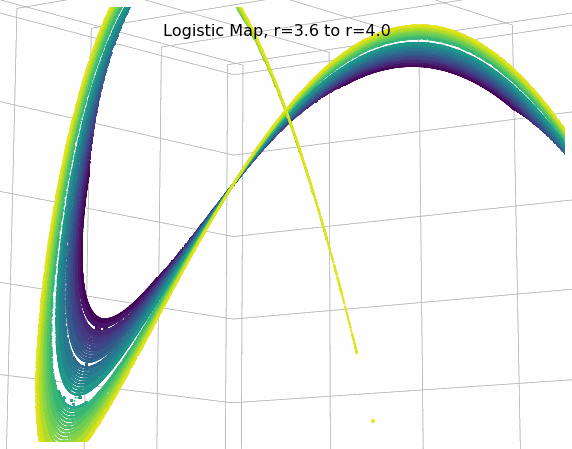
Animate the 3D phase diagram of the logistic map to reveal the strange attractor's structure:

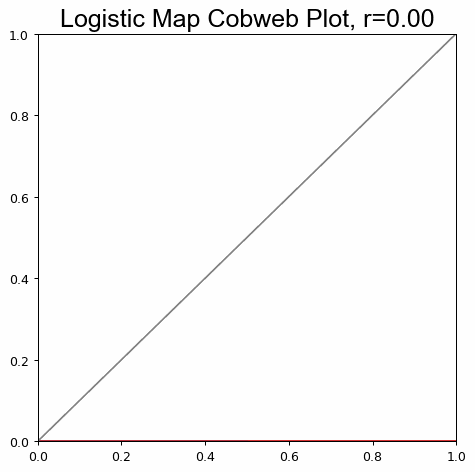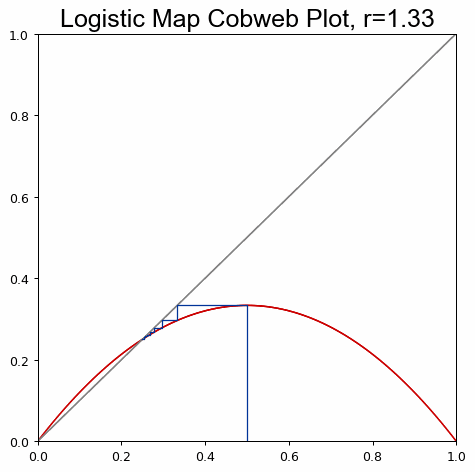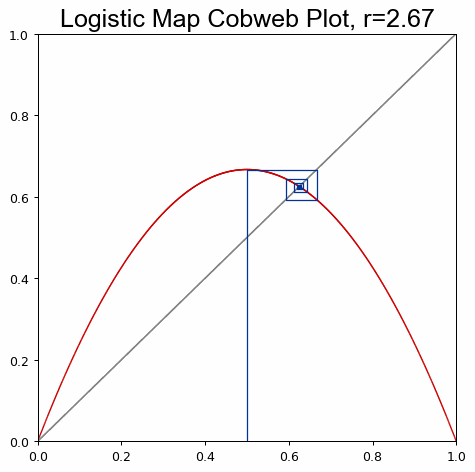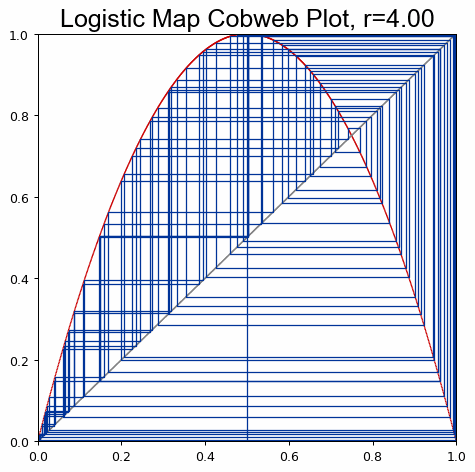
Animate a cobweb plot of the logistic map's parameter space to explore sensitivity and behavior:

Or define your own model and simulate it with pynamical.