A Universe of Sorts

Siddharth Bhat

• Please leave feedback!
• Vidcall/Hang out
• Reach me: [email protected]
• github
• math.se
• resume
• reading list/TODO
• Here is the RSS feed for this page

Covariant hom is left exact

Internal versus External semidirect products

Say we have an inner semidirect product. This means we have subgroups $N, K$ such that $NK = G$, $N$ normal in $G$ and $N \cap K = { e }$. Given such conditions, we can realize $N$ and $K$ as a semidirect product, where the action of $K$ on $N$ is given by conjugation in $G$. So, concretely, let's think of $N$ (as an abstract group) and $K$ (as an abstract group) with $K$ acting on $N$ (by conjugation inside $G$). We write the action of $k$ on $n$ as $n^k \equiv knk^{-1}$. We then have a homomorphism $\phi: N \ltimes K \rightarrow G$ given by $\phi((n, k)) = nk$. To check this is well-defined, let's take $s, s' \in N \ltimes K$, with $s \equiv (n, k)$ and $s' \equiv (n', k')$. Then we get:

$$ \begin{aligned} &\phi(ss') = \ &=\phi((n, k) \cdot (n', k')) \ &\text{definition of semidirect product via conjugation:} \ &= \phi((n {n'}^k, kk')) \ &\text{definition of $\phi$:} \ &= n n'^{k} kk' \ &\text{definition of $n'^k = k n' k^{-1}$:} \ &= n k n'k^{-1} k k' \ &= n k n' k' \ &= \phi(s) \phi(s') \end{aligned} $$

So, $\phi$ really is a homomorphism from the external description (given in terms of the conjugation) and the internal description (given in terms of the multiplication).

We can also go the other direction, to start from the internal definition and get to the conjugation. Let $g \equiv nk$ and $g' \equiv n'k'$. We want to multiply them, and show that the multiplication gives us some other term of the form $NK$:

$$ \begin{aligned} gg' \ &= (n k) (n' k') \ &= n k n' k' \ &= \text{insert $k^{-1}k$: } \ &= n k n' k^{-1} k k' \ &= n (k n' k^{-1}) k k' \ &= \text{$N$ is normal, so $k n' k^{-1}$ is some other element $n'' \in N$:} \ &= n n'' k k' \ &= N K \end{aligned} $$

So, the collection of elements of the form $NK$ in $G$ is closed. We can check that the other properties hold as well.

Splitting of semidirect products in terms of projections

Say we have an exact sequence that splits:

$$ 0 \rightarrow N \xrightarrow{i} G \xrightarrow{\pi} K \rightarrow 0 $$

with the section given by $s: K \rightarrow G$ such that $\forall k \in K, \pi(s(k)) = k$. Then we can consider the map $\pi_k \equiv s \circ pi: G \rightarrow G$. See that this firsts projects down to $K$, and then re-embeds the value in $G$. The cool thing is that this is in fact idempotent (so it's a projection!) Compute:

$$ \begin{aligned} &\pi_k \circ \pi_k \ &= (s \circ \pi) \circ (s \circ \pi ) \ &= s \circ (\pi \circ s) \circ \pi ) \ &= s \circ id \circ \pi \ &= s \circ \pi = \pi_k \ \end{aligned} $$

So this "projects onto the $k$ value". We can then extract out the $N$ component as $\pi_n: G \rightarrow G; \pi_n(g) \equiv g \cdot \pi(k)^{-1}$.

Tensor is right exact

Consider an exact sequence

$$ 0 \rightarrow A \xrightarrow{f} B \xrightarrow{g} C \rightarrow 0 $$

We wish to consider the operation of tensoring with some ring $R$. For a given ring morphism $h: P \rightarrow Q$ this induces a new morphism $R \otimes h: R \otimes A \rightarrow R \otimes B$ defined by $h(r \otimes a) \equiv r \otimes h(a)$.

So we wish to contemplate the sequence:

$$ R \otimes A \xrightarrow{R \otimes f} R \otimes B \xrightarrow{R \otimes g} R \otimes C $$

To see if it is left exact, right exact, or both. Consider the classic sequence of modules over $\mathbb Z$:

A detailed example

$$ 0 \rightarrow 2\mathbb Z \xrightarrow{i} \mathbb Z \xrightarrow{\pi} \mathbb Z / \mathbb 2Z \rightarrow 0 $$

Where $i$ is for inclusion, $\pi$ is for projection. This is an exact sequence, since it's of the form kernel-ring-quotient. We have three natural choices to tensor with: $\mathbb Z, \mathbb 2Z, \mathbb Z/\mathbb 2Z$. By analogy with fields, tensoring with the base ring $\mathbb Z$ is unlikely to produce anything of interest. $\mathbb 2Z$ maybe more interesting, but see that the map $1 \in \mathbb Z \mapsto 2 \in 2 \mathbb Z$ gives us an isomorphism between the two rings. That leaves us with the final and most interesting element (the one with torsion), $\mathbb Z / \mathbb 2Z$. So let's tensor by this element:

$$ \mathbb Z/2\mathbb Z \otimes 2\mathbb Z \xrightarrow{i'} \mathbb Z/2\mathbb Z \otimes \mathbb Z \xrightarrow{\pi'} \mathbb Z/2\mathbb Z \otimes \mathbb Z / \mathbb 2Z $$

• See that $\mathbb Z/2\mathbb Z \otimes 2 \mathbb Z$ has elements of the form $(0, *) = 0$, We might imagine that the full ring collapses since $1 \otimes 2k) = 2(1 \otimes k) = 2 \otimes k = 0$ (since $2 = 0$ in $\mathbb Z/2\mathbb Z$). But this in fact incorrect! Think of the element $1 \otimes 2$. We cannot factorize this as $2(1 \otimes 1)$ since $1 \not \in 2 \mathbb Z$. So we have the element $1 \otimes 2 \in \mathbb Z/2\mathbb Z / \times 2 \mathbb Z$.
• See that $\mathbb Z/2\mathbb Z \otimes \mathbb Z \simeq \mathbb Z/2\mathbb Z$: Factorize $(k, l) = l(k, 1) = (kl, 1) \simeq \mathbb Z/2 \mathbb Z$.
• Similarly, see that $\mathbb Z/2\mathbb Z \otimes \mathbb Z/2\mathbb Z \simeq \mathbb Z/2\mathbb Z$. Elements $0 \otimes 0, 0 \otimes 1, 1 \otimes 0 \simeq 0$ and $1 \otimes 1 \simeq 1$.
• In general, Let's investigate elements $a \otimes b \in \mathbb Z/n\mathbb Z \otimes \mathbb Z/m\mathbb mZ$ . We can write this as $ab 1 \otimes 1$. The $1 \otimes 1$ gives us a "machine" to reduce the number by $n$ and by $m$. So if we first reduce by $n$, we are left with $r$ (for remained) for some $ab = \alpha n + r$. We can then reduce $r$ by $m$ to get $ab = \alpha n + \beta m + r'$. So if $r' = 0$, then we get $ab = \alpha n + \beta m$. But see that all elements of the form $\alpha n + \beta m$ is divisible by $gcd(n, m)$. Hence, all multiples of $gcd(n, m)$ are sent to zero, and the rest of the action follows from this. So we effectively map into $\mathbb Z/ gcd(m, n) \mathbb Z$
• In fact, we can use the above along with (1) write finitely generated abelian groups as direct sum of cyclic groups, (2) tensor distributes over direct sum. This lets us decompose tensor products of all finitely generated abelian groups into cyclics.
• This gives us another heuristic argument for why $\mathbb Z \times \mathbb Z/2\mathbb Z \simeq \mathbb Z/2 \mathbb Z$. We should think of $\mathbb Z$ as $\mathbb Z/\mathbb \infty Z$, since we have "no torsion" or "torsion at infinity". So we get the tensor product should have $gcd(2, \infty) = 2$.
• Now see that the first two components of the tensor give us a map from $\mathbb Z/2\mathbb Z \otimes \mathbb 2Z \xrightarrow{i} \mathbb Z/2\mathbb Z \otimes \mathbb Z$ which sends:

$$ \begin{aligned} &x \otimes 2k \mapsto x \otimes 2k \in \mathbb Z/2\mathbb Z \otimes \mathbb Z \ &= 2 (x \otimes k) \ &= (2x \otimes k) \ &=0 \otimes k = 0 \end{aligned} $$

• This map is not injective, since this map kills everything! Intuitively, the "doubling" that is latent in $2\mathbb Z$ is "freed" when injecting into $\mathbb Z$. This latent energy explodes on contant with $\mathbb Z/2 \mathbb Z$ giving zero. So, the sequence is no longer left-exact, since the map is not injective!

• So the induced map is identically zero! Great, let's continue, and inspect the tail end $ \mathbb Z/2\mathbb Z \otimes \mathbb Z \xrightarrow{\pi} \mathbb Z/2\mathbb Z \otimes \mathbb Z / \mathbb 2Z$. Here, we sent the element $(x, y) \mapsto (x, y \mod 2)$. This clearly gives us all the elements: For example, we get $0 \otimes 0$ as the preimage of $0 \times 2k$ and we get $1 \otimes 1$ as the preimage of (predictably) $1 \otimes (2k+1)$. Hence, the map is surjective.

So finally, we have the exact sequence:

$$ \mathbb Z/2\mathbb Z \otimes 2\mathbb Z \xrightarrow{i'} \mathbb Z/2\mathbb Z \otimes \mathbb Z \xrightarrow{\pi'} \mathbb Z/2\mathbb Z \otimes \mathbb Z / \mathbb 2Z \rightarrow 0 $$

We do NOT have the initial $(0 \rightarrow \dots)$ since $i'$ is no longer injective. It fails injectivity as badly as possible, since $i'(x) = 0$. Thus, tensoring is RIGHT EXACT. It takes right exact sequences to right exact sequences!

The general proof

Given the sequence:

$$ A \xrightarrow{i} B \xrightarrow{\pi} C \rightarrow 0 $$

We need to show that the following sequence is exact:

$$ R \otimes A \xrightarrow{i'} R \otimes B \xrightarrow{\pi'} R \otimes C \rightarrow 0 $$

• First, to see that $\pi'$ is surjective, consider the basis element $r \otimes c \in R \otimes C$. Since $\pi$ is surjective, there is some element $b \in B$ such that $\pi(b) = c$. So the element $r \otimes b \in B$ maps to $r \otimes c$ by $\pi'$; $\pi'(r \otimes b) = r \otimes \pi(b) = r \otimes c$ (by definition of $\pi$, and choice of $b$). This proves that $B \xrightarrow{\pi'} R \otimes C \rightarrow 0$ is exact.

• Next, we need to show that $im(i') = ker(\pi')$.

• To show that $im(i') \subseteq ker(\pi')$, consider an arbitrary $r \otimes a$. Now compute:

$$ \begin{aligned} &\pi'(i'(r \otimes a)) \ &= \pi'(r \otimes i(a)) \ &= r \otimes \pi(i(a)) & \text{By exactness of $A \xrightarrow{i} B \xrightarrow{\pi} C$, $\pi(i(a)) = 0$:} \ &= r \otimes 0 \ &= 0 \end{aligned} $$ So we have that any element in $i'(r \otimes a) \in im(i')$ is in the kernel of $\pi'$.

Next, let's show $ker(\pi') \subseteq im(i')$. This is the "hard part" of the proof. So let's try a different route. I claim that if $im(i') = ker(\pi')$ iff $coker(i') = R \otimes C$. This follows because:

$$ \begin{aligned} &coker(i) = (R \otimes B)/ im(i') \ & \text{Since } im(i') = ker(\pi') &= (R \otimes B)/ker(\pi') \ & \text{Isomorphism theorem: } \ &= im(\pi') \ & \text{$\pi'$ is surjective: } \ &= R \otimes C \end{aligned} $$

Since each line was an equality, if I show that $coker(i) = R \otimes C$, then I have that $im(i') = ker(\pi')$. So let's prove this:

$$ \begin{aligned} &coker(i) = (R \otimes B)/ im(i') \ &= (R \otimes B)/i'(R \otimes A) \ & \text{Definition of $i'$: } \ &= (R \otimes B)/(R \otimes i(A)) \ \end{aligned} $$

I claim that the $(R \otimes B)/( R \otimes i(A)) \simeq R \otimes (B/i(A))$ (informally, "take $R$ common"). Define the quotient map $q: B \rightarrow B/i(A)$. This is a legal quotient map because $i(A) = im(i) \simeq ker(\pi)$ is a submodule of $B$.

$$ \begin{aligned} q : B \rightarrow B/i(A) \ f: R \otimes B \rightarrow \rightarrow R \otimes (B / i(A)) \ f(r \otimes b) = r \otimes q(b) \ r \otimes b \in R \otimes B \xrightarrow{f = R \otimes q } r \otimes q(b) \in R \otimes B/i(A) \end{aligned} $$

Let's now study $ker(f)$. It contains all those elements such that $r \otimes q(b) = 0$. But this is only possible if $q(b) = 0$. This means that $b \in i(A) = im(i) = ker(\pi)$. Also see that for every element $r \otimes (b + i(A)) \in R \otimes (B/i(A))$, there is an inverse element $r \otimes b \in R \otimes B$. So, the map $f$ is surjective. Hence, $im(f) \simeq R \otimes (B/i(A))$. Combining the two facts, we get:

$$ \begin{aligned} &domain(f)/ker(f) \simeq im(f) \ &(R \otimes B)/(R \otimes (B/i(A))) \simeq R \otimes (B/i(A)) &coker(i) = (R \otimes B)/(R \otimes (B/i(A))) \simeq R \otimes (B/i(A)) = R \otimes C \end{aligned} $$

Hence, $coker(i) \simeq R \otimes C$.

• Reference: Kyle Miller's notes on the exactness of the tensor product

Semidirect product as commuting conditions

Recall that in $N \ltimes K = G$, $N$ is normal. This is from the mnemonic that it looks like $N \triangleleft G$, or from the fact that the acting/twisting subgroup $K$ is a fish that wants to "eat"/act on the normal subgroup $N$.

So, we have $knk^{-1} \in N$ as $N$ is normal, thus $knk^{-1} = n'$. This can be written as $kn = n'k$. So:

• When commuting, the element that gets changed/twisted in the normal subgroup. This is because the normal subgroup has the requisite constraint on it to be twistable.
• The element that remains invariant is the actor.

In the case of translations and rotations, it's the translations that are normal. This can be seen either by noticing that they are abelian, and are thus normal, while rotations don't "look normal". Alternatively, one can try to consider translate-rotate versus rotate-translate.

- First rotating by $r$ and then translating by $t$ along the x-axis has the same effect as first translating by $t'$ at 45 degrees to the x-axis, and then rotating by the **same** r.

• This begs the question, is there some other translation t'' and some other rotation r'' such that t''; r'' (t'' first, r'' next) has the same effect as r;t (r first, t next)?

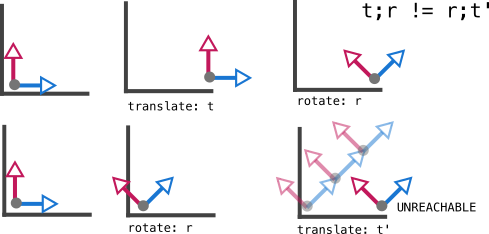
• First let's translate by $t$ along the x-axis and then rotating by $r$. Now let's think, if we wanted to rotate and then translate, what rotation would we start with? it would HAVE TO BE $r$, since there's no other way to get the axis in such an angle in the final state. But if we rotate by $r$, then NO translation can get us to the final state we want. So, it's impossible to find a rotation;translation pair that mimics our starting translation;rotation.

Exact sequences for semidirect products; fiber bundles

Fiber bundles

In the case of a bundle, we have a sequence of maps $F \rightarrow E \rightarrow B$ where $F$ is the fiber space (like the tangent space at the identity $T_eM$). $E$ is the total space (the bundle $TM$), and $B$ is the base space (the manifold $M$). We require that the inverse of the projection $\pi^{-1}: B \rightarrow E$ locally splits as product $\pi^{-1}(U) \simeq U \times F$.

Semidirect products

In a semidirect product $N \ltimes K$, we have that $N$ is normal (because the fish wants to eat the normal subgroup $N$ / the symbol looks like $N \triangleleft G$ which is how we denote normality). Thus, we can only quotient by $N$, leaving us with $K$. This is captured by the SES:

$$ 0 \rightarrow N \rightarrow N \ltimes K \xrightarrow{\pi} K \rightarrow 0 $$

• We imagine this as a bundle, with base space $M=K$, bundle $TM=N \ltimes K$, and fiber space (like, tangent space at the identity, say) $T_e M = N$.

• Furthermore, this exact sequence splits; So there is a map $s: K \rightarrow N \ltimes K$ ($s$ for "section/split") such that $\forall k, \pi(s(k)) = k$. To see that this is true, define $s(k) \equiv (e, k)$. Since all actions of $K$ fix the identity $e \in N$, we have $s(k)s(k') = (e, k) (e, k') = (e, kk') = s(kk')$ so this is a valid map. To see that $\pi$ is its inverse, just act $\pi$; $\pi(s(k)) = \pi(e, k) = k$.

Relationship to gauges

Let $X$ be the space of all states. Let $O$ be a group action whose orbits identify equivalent states. So the space of "physical states" or "states that describe the same physical scenario" is the orbit of $X$ under $O$, or $X/O$. Now, the physical space $X/O$ is acted upon by some group $G$. If we want to "undo the quotienting" to have $G$ act on all of $X$, then we need to construct $G \ltimes O$. $G$ is normal here because $O$ already knows how to act on the whole space; $G$ does not, so $O$ needs to "guide" the action of $G$ by acting on it. The data needed to construct $G \ltimes O$ is a connection. Topologically, we have $X \rightarrow X/O$ and $G \curvearrowright X/O$. We want to extend this to $(G \ltimes O) \curvearrowright X$. We imagine this as:

*1| #1 | @1  X
*2| #2 | @2
*3| #3 | @3
  | |  |
  | v  |
* | #  | @ X/H

where the action of $H$ permutes amongst the fibers of *, #, @. Next, we have an action of $G$ on $X/H$:

*1| #1 | @1  X
*2| #2 | @2
*3| #3 | @3
  | |  |
  | v  |
* | #  | @ [X/H] --G--> # | @ | *

We need to lift this action of H the H-orbits. This is precisely the data a connection gives us (why?) I guess the intuition is that the orbits of $X$ are like the tangent spaces where $X \rightarrow X/O$ is the projection from the bundle into the base space, and the $G$ is a curve that tells us what the "next point" we want to travel to from the current point. The connection allows us to "lift" this to "next tangent vector". That's quite beautiful.

We want the final picture to be:

*1| #1 | @1  X          #2| @2|                    
*2| #2 | @2    --G-->   #1|   |   
*3| #3 | @3             #3|   | 
  | |  |                  |   | 
  | v  |                  |   |  
* | #  | @ [X/H] --G--> # | @ | *

If sequence splits then semidirect product

Consider the exact sequence

$$ 0 \rightarrow N \xrightarrow{\alpha} G \xrightarrow{\pi} H \rightarrow 0 $$

• We want to show that if there exists a map $s: H \rightarrow G$ such that $\forall h, \pi(s(h)) = h$ (ie, $\pi \circ s = id$), then G$ \simeq N \ltimes H$. So the splitting of the exact sequence decomposes $G$ into a semidirect product.
• The idea is that elements of $G$ have an $N$ part and a $K$ part. We can get the $K$ part by first pushing into $K$ using $\pi$ and then pulling back using $s$. So define $k: G \rightarrow G; k(g) \equiv s(\pi(g))$. This gives us the "K" part. To get the $N$ part, invert the "k part" to annihiliate it from $G$. So define a map $n: G \rightarrow G; n(g) \equiv g k(g)^{-1} = g k(g^{-1})$.
• See that the image of $n$ lies entirely in the kernel of $\pi$, or the image of $n$ indeed lies in $N$. This is a check:

$$ \begin{aligned} &\pi(n(g)) \ = \pi(g k(g^{-1})) \ = \pi(g) \pi(k(g^{-1})) \ = \pi(g) \pi(s(\pi(g^{-1}))) \ = \text{$\pi(s(x)) = x$:}\ = \pi(g) \pi(g^{-1}) = e \end{aligned} $$

• Hence, the image of $n$ is entirely in the kernel of $\pi$. But the kernel of $\pi$ is isomorphic to $N$, and hence the image of $n$ is isomorphic to $N$. So we've managed to decompose an element of $G$ into a $K$ part and an $N$ part.
• Write $G$ as $N \ltimes K$, by the map $\phi: G \rightarrow N \ltimes K; \phi(g) = (n(g), k(g))$. Let's discover the composition law.

$$ \begin{aligned} &\phi(gh) =^? \phi(g) \phi(h) \ &(n(gh), k(gh)) =^? (n(g), k(g)) (n(h), k(h)) \ &(ghk((gh)^{-1}), k(gh)) =^? (gk(g^{-1}), k(g)) (hk(h^{-1}), k(h)) \ \end{aligned} $$

We need the second to be $k(gh) = k(g) k(h)$, so that composes in an entirely straightforward fashion. For the other component, we need:

$$ \begin{aligned} &ghk((gh)^{-1}) =^? gk(g^{-1}) \cdot hk(h^{-1}) \ &ghk((gh)^{-1}) =^? gk(g^{-1}) k(g) \cdot hk(h^{-1}) k(g^{-1}) \ &ghk((gh)^{-1}) =^? g [k(g^{-1}) k(g)] \cdot h [k(h^{-1}) k(g^{-1})] \ &ghk((gh)^{-1}) =^? g \cdot h k((gh)^{-1}) \ &ghk((gh)^{-1}) = gh k((gh)^{-1}) \ \end{aligned} $$

So we need the $n$ of $h$ to be twisted by the $k$ component of $g$ by a conjugation. So we define the semidirect structure as:

$$ \begin{aligned} (n(g), k(g)) \cdot (n(h), k(h)) \equiv (n(g) k(g) n(h) k(g)^{-1}, k(g) k(h)) \ &= (n(g) n(h)^{k(g)}, k(g) k(h)) \end{aligned} $$

We've checked that this works with the group structure. So we now have a morphism $\phi: G \rightarrow N \ltimes K$. we need to check that it's an isomorphism, so we need to make sure that this has full image and trivial kernel.

• Full image: Let $(n, k) \in N \ltimes K$. Create the element $g = \alpha(n) s(k) \in G$. We get $\pi(g) = \pi(\alpha(n)s(k)) = \pi(\alpha(n)) \pi(s(k)) = e k = k$. We get $n(g) = g k$

• physics.se

Intro to topological quantum field theory

• Once again, watching a videos for shits and giggles.
• Geometrically, we cut and paste topological indices / defects.
• QFT in dimensions n+1 (n space, 1 time)
• Manifold: $X^n$. Can associate a hilbert space of states $H_x$.
• Space of wave functions on field space.
• Axioms of hilbert space: (1) if there is no space, the hilbert space $H_\emptyset$ for it is the complex numbers. (2) If we re-orient the space, the hilbert space becomes the dual $H_{-X} = H_X^\star$. (3) Hilbert space over different parts is the tensor product: $H_{X \cup Y} = H_X \otimes H_Y$.
• We want arbitrary spacetime topology. We start at space $X$, and we end at a space $Y$. The space $X$ is given positive orientation to mark "beginning" and $Y$ is given negative orientation to mark "end". We will have a time-evolution operator $\Phi: H_X \rightarrow H_Y$.
• We have a composition law of gluing: Going from $X$ to $Y$ and then from $Y$ to $Z$ is the same as going from $X$ to $Z$. $\phi_{N \circ M} = \phi_N \circ \phi_M$.
• If we start and end at empty space, then we get a linear map $\Phi: H_\emptyset \rightarrow H_\emptyset$ which is a linear map $\Phi: \mathbb C \rightarrow \mathbb C$, which is a fancy way to talk about a complex number (scaling)
• If we start with an empty set and end at $Y$, then we get a function $\Phi: H_\emptyset \rightarrow H_Y \simeq \mathbb C \rightarrow \mathbb Y$. But this is the same as picking a state, for example, $\Phi(1) \in H_Y$ [everything else is determined by this choice].
• If a manifold has two sections $X$ and $-X$, we can glue $X$ to $-X$ to get the trace.
• Quantum mechanics is 0 + 1 TQFT (!)
• TQFT of 1+1 dimensions.
• Take a circle: $S^1 \rightarrow H$. Let $H$ be finite dimensional.
• A half-sphere has a circle as boundary. So it's like $H_\emptyset \rightarrow H_{S^1}$. This is the ket $|0\rangle$.
• This is quite a lot like a string diagram...
• Frobenius algebra
• Video: IAS PiTP 2015

Spectral norm of Hermitian matrix equals largest eigenvalue (WIP)

Define $||A|| \equiv \max { ||Ax|| : ||x|| = 1 }$. Let $A$ be hermitian. We wish to show that $||A||$ is equal to the largest eigenvalue. The proof idea is to consider the eigenvectors $v[i]$ with eigenvalue $\lambda[i]$ with largest eigenvalue $v^\star$ of eigenvalue $\lambda^$ and claim that $||Av^\star|| = \lambda^$ is maximal.

Non examples of algebraic varieties

It's always good to have a stock of non-examples.

Line with hole: Algebraic proof

The set of points $V \equiv { (t, t) : t \neq 42, t \in \mathbb R } \subseteq mathbb R^2$ is not a variety. To prove this, assume it is a variety defined by equations $I(V)$. Let $f(x, y) \in I(V) \subseteq \mathbb R[x, y]$. Since $f$ vanishes on $V$, we must have $f(a, a) = 0$ for all $a \neq 42$ (since $(a, a) \in V$ for all $a \neq 42$). So create a new function $g(a) \equiv (a, a)$. Now $f \circ g: \mathbb R \rightarrow \mathbb R = f(g(a)) = f(a, a) = 0$. This polynomial (it is a composition of polynomial, and is thus a polynomial) has infinitely many zeroes, and is thus identically zero. So, $f(g(a)) = 0$, So $f(a, a) = 0$ for all $a$. In particular, $f(42, 42) = 0$ for all equations that define $V$, hence $(42, 42) \in I(V)$. But this does not give us the variety $V$. Hence $V$ is not a variety.

Line with hole: Analytic proof

The set of points $V \equiv { (t, t) : t \neq 42, t \in \mathbb R } \subseteq mathbb R^2$ is not a variety. To prove this, assume it is a variety defined by equations $I(V)$. Let $f(x, y) \in I(V) \subseteq \mathbb R[x, y]$. Since $f$ vanishes on $V$, we must have $f(a, a) = 0$ for all $a \neq 42$ (since $(a, a) \in V$ for all $a \neq 42$). Since $f$ is continuous, $f$ preserves limits. Thus, $\lim_{x \to 42} f(x, x) = f(\lim_{x \to 42} (x, x))$. The left hand side is zero, hence the right hand size must be zero. Thus, $f(42, 42) = 0$. But this can't be, because $(42, 42) \not \in V$.

$\mathbb Z$

The set $\mathbb Z$ is not an algebraic variety. Suppose it is, and is the zero set of a collection of polynomials ${ f_i }$. Then for some $f_i$, they must vanish on at least all of $\mathbb Z$, and maybe more. This means that $f_i(z) = 0$ for all $z \in \mathbb Z$. But a degree $n$ polynomial can have at most $n$ roots, unless it is the zero polynomial. Since $f_i$ does not have a finite number of roots, $f_i = 0$. Thus, all the polynomials are identically zero, and so their zero set is not $\mathbb Z$; it is all of $\mathbb R$.

The general story

In general, we are using a combinatorial fact that a $n$ degree polynomial has at most $n$ roots. In some cases, we could have used analytic facts about continuity of polynomials, but it suffices to simply use combiantorial data which I find interesting.

Nilradical is intersection of all prime ideals

Nilradical is contained in intersection of all prime ideals

Let $x \in \sqrt 0$. We must show that it is contained in all prime ideals. Since $x$ is in the nilradical, $x$ is nilpotent, hence $x^n = 0$ for some $n$. Let $p$ be an arbitrary prime ideal. Since $0 \in p$ for all prime ideals, we have $x^n = 0 \in p$ for $x$. This means that $x^n = x \cdot x^{n-1} \in p$, and hence $x \in p \lor x^{n-1} \in p$. If $x \in p$ we are done. If $x^{n-1} \in p$, recurse to get $x \in p$ eventually.

Proof 1: Intersection of all prime ideals is contained in the Nilradical

Let $f$ be in the intersection of all prime ideals. We wish to show that $f$ is contained in the nilradical (that is, $f$ is nilpotent). We know that $R_f$ ($R$ localized at $f$) collapses to the zero ring iff $f$ is nilpotent. So we wish to show that the sequence:

$$ \begin{aligned} 0 \rightarrow R_f \rightarrow 0 \end{aligned} $$

is exact. But exactness is a local property, so it suffices to check against each $(R_f)_m$ for all maximal ideals $m$. Since $(R_f)_m = (R_m)_f$ (localizations commute), let's reason about $(R_m)_f$. We know that $R_m$ is a local ring as $m$ is prime (it is maximal), and thus $R_m$ has only a single ideal $m$. Since $f \in m$ for all maximal ideal $m$ (since $f$ lives in the intersection of all prime ideals), localizing at $f$ in $R_m$ blows up the only remaining ideal, collapsing us the ring to give us the zero ring. Thus, for each maximal ideal $m$, we have that:

$$ \begin{aligned} 0 \rightarrow (R_f)_m \rightarrow 0 \end{aligned} $$

is exact. Thus, $0 \rightarrow R_f \rightarrow 0$ is exact. Hence, $f$ is nilpotent, or $f$ belongs to the nilradical.

Proof 2: Intersection of all prime ideals is contained in the Nilradical

• Quotient the ring $R$ by the nilradical $N$.
• The statement in $R/N$ becomes "in a ring with no ninpotents, intersection of all primes is zero".
• This means that every non-zero element is not contained in some prime ideal. Pick some arbitrary element $f \neq 0 \in R/N$. We know $f$ is not nilpotent, so we naturally consider $S_f \equiv { f^i : i \in \mathbb N }$.
• The only thing one can do with a multiplicative subset like that is to localize. So we localize the ring $R/N$ at $S$.
• If all prime ideals contain the function $f$, then localizing at $f$ destroys all prime ideals, thus blows up all maximal ideals, thereby collapsing the ring into the zero ring (the ring has no maximal ideals, so the ring is the zero ring).
• Since $S^{-1} R/N = 0$, we have that $0 \in S$. So some $f^i = 0$. This contradicts the assumption that no element of $R/N$ is nilpotent. Thus we are done.

Lemma: $S$ contains zero iff $S^{-1} R = 0$

• (Forward): Let $S$ contain zero. Then we must show that $S^{-1} R = 0$. Consider some element $x/s \in S^{-1} R$. We claim that $x = 0/1$. To show this, we need to show that there exists an $s' \in S$ such that $xs'/s = 0s'/1$. That is, $s'(x \cdot 1 - 0 \cdot s) = 0$. Choose $s' = 0$ and we are done. Thus every element is $S^{-1}R$ is zero if $S$ contains zero.

• (Backward): Let $S^{-1} R = 0$. We need to show that $S$ contains zero. Consider $1/1 \in S^{-1} R$. We have that $1/1 = 0/1$. This means that there is an $s' \in S$ such that $s'1/1 = s'0/1$. Rearranging, this means that $s'(1 \cdot 1 - 1 \cdot 0) = 0$. That is, $s'1 = 0$, or $s' = 0$. Thus, the element $s'$ must be zero for $1$ to be equal to zero. Hence, for the ring to collapse, we must have $0 = s' \in S$. So, if $S^{-1}R = 0$, then $S$ contains zero.

Exactness of modules is local

We wish to show that for some ring $R$ and modules $K, L, M$ a sequence $K \rightarrow L \rightarrow M$ is exact iff $K_m \rightarrow L_m \rightarrow M_m$ is exact for every maximal ideal $m \subset R$. This tells us that exactness is local.

Quotient by maximal ideal gives a field

Quick proof

Use correspondence theorem. $R/m$ only has the images of $m, R$ as ideals which is the zero ideal and the full field.

Element based proof

Let $x + m \neq 0$ be an element in $R/m$. Since $x + m \neq 0$, we have $x \not in m$. Consider $(x, m)$. By maximality of $m$, $(x, m) = R$. Hence there exist elements $a, b \in R$ such that $xa + mb = 1$. Modulo $m$, this read $xa \equiv 1 (\text{mod}~$m$)$. Thus $a$ is an inverse to $x$, hence every nonzero element is invertible.

Ring of power series with infinite positive and negative terms

If we allow a ring with elements $x^i$ for all $-\infty < x < \infty$, for notation's sake, let's call it $R[[[x]]]$. Unfortunately, this is a badly behaved ring. Define $S \equiv \sum_{i = -\infty}^\infty x^i$. See that $xS = S$, since multiplying by $x$ shifts powers by 1. Since we are summing over all of $\mathbb Z$, $+1$ is an isomorphism. Rearranging gives $(x - 1)S = 0$. If we want our ring to be an integral domain, we are forced to accept that $S = 0$. In the Barvinok theory of polyhedral point counting, we accept that $S = 0$ and exploit this in our theory.

Mean value theorem and Taylor's theorem. (TODO)

I realise that there are many theorems that I learnt during my preparation for JEE that I simply don't know how to prove. This is one of them. Here I exhibit the proof of Taylor's theorem from Tu's introduction to smooth manifolds.

Taylor's theorem: Let $f: \mathbb R \rightarrow \mathbb R$ be a smooth function, and let $n \in \mathbb N$ be an "approximation cutoff". Then there exists for all $x_0 \in \mathbb R$ a smooth function $r \in C^{\infty} \mathbb R$ such that: f(x) = f(x_0) + (x - x_0) f'(x_0)/1! + (x - x_0)^2 f'(x_0)/2! + \dots + (x - x_0)^n f^{(n)'}(x_0)/n! + (x - x_0)^{n+1} r

We prove this by induction on $n$. For $n = 0$, we need to show that there exists an $r$ such that $f(x) = f(x_0) + r$. We begin by parametrising the path from $x_0$ to $x$ as $p(t) \equiv (1 - t) x_0 + tx$. Then we consider $(f \circ p)'$:

$$ \begin{aligned} &\frac{f(p(t))}{dt} = \frac{df((1 - t) x_0) + tx)}{dt} \ &= (x - x_0) \frac{df((1 - t)x_0) + tx)}{dx} \end{aligned} $$

Integrating on both sides with limits $t=0, t=1$ yields:

$$ \begin{aligned} &\int_0^1 \frac{df(p(t))}{dt} dt = \int_0^1 (x - x_0) \frac{df((1 - t)x_0) + tx)}{dx} dt \ f(p(1)) - f(p(0)) = (x - x_0) \int_0^1 \frac{df((1 - t)x_0) + tx)}{dx} dt \ f(x) - f(x_0) = (x - x_0) g1 \ \end{aligned} $$

where we define $g1 \equiv \int_0^1 \frac{df((1 - t)x_0) + tx)}{dx} dt $ where the $g1$ witnesses that we have the first derivative of $f$ in its expression. By rearranging, we get:

$$ \begin{aligned} f(x) - f(x_0) = (x - x_0) g1 \ f(x) = f(x_0) + (x - x_0) g1 \ \end{aligned} $$

If we want higher derivatives, then we simply notice that $g1$ is of the form:

$$ \begin{aligned} g1 \equiv \int_0^1 f'((1 - t)x_0) + tx) dt \ g1 \equiv \int_0^1 f'((1 - t)x_0) + tx) dt \ \end{aligned} $$

Cayley Hamilton

I find the theorem spectacular, because while naively the vector space $M_n(F)$ has dimension $n^2$, Cayley-Hamilton tells us that there's only $n$ of $M^0, M^1, \dots$ are enough to get linear dependence. However, I've never known a proof of Cayley Hamilton that sticks with me; I think I've found one now.

For any matrix $A$, the adjugate has the property:

$$ A adj(A) = det(A) I $$

Using this, Consider the matrix $P_A \equiv xI - A$ which lives in $End(V)[x]$, and its corresponding determinant $p_A(x) \equiv det(P_A) = det(xI - A)$.

We have that

$$ P_A adj(P_A) = det(P_A) I \ (xI - A) adj(xI - A) = det(xI - A) I = p_A(x) I \ $$

If we view this as an equation in $End(V)[x]$, it says that $p_A$ has a factor $xI - A$. This means that $x = A$ is a zero of $p_A(X)$. Thus, we know that $A$ satisfies $p_A(x)$, hence $A$ satisfies its own characteristic polynomial!

The key is of course the adjugate matrix equation that relates the adjugate matrix to the determinant of $A$.

Adjugate matrix equation

• Let $A'(i, j)$ be the matrix $A$ with the $i$ th row and $j$ column removed.
• Let $C[i, j] \equiv (-1)^{i+j} det(A'(i, j))$ be the determinant of the $A'(i, j)$ matrix.
• Let define $adj(A) \equiv C^T$ to be the transpose of the cofactor matrix. That is, $adj(A)[i, j] = C[j, i] = det(A'(j, i))$.
• Call $D \equiv A adj(A)$. We will now compute the entries of $Z$ when $i = j$ and when $i \neq j$. We call it $D$ for diagonal since we will show that $D$ is a diagonal matrix with entry $det(A)$ on the diagonal.
• First, compute $D[i, i]$ (I use einstein summation convention where repeated indices are implicitly summed over):

$$ \begin{aligned} = D[i, i] = (A adj(A))[i, i] \ &= A[i, k] adj(A) [k, i] \ &= A[i, k] (-1)^{i+k} det(A'[k, i]) \ &= det(A) \end{aligned} $$

The expression $A[i, k] det(A'[k, i])$ is the determinant of $A$ when expanded along the row $i$ using the Laplace expansion.

Next, let's compute $D[i, j]$ when $i \neq j$:

$$ \begin{aligned} D[i, j] = (A adj(A))[i, j] \ &= A[i, k] adj (A)[k, j] \ & = A[i, k] (-1)^{k+j} det(A'[k, j]) \ & = A[i, k] (-1)^{j+k} det(A'[k, j]) \ & = det(Z) \end{aligned} $$

This is the determinant of a new matrix $Z$ (for zero), such that the $j$th row of $Z$ is the $i$th row of $A$. More explicitly:

$$ \begin{aligned} Z[l, :] \equiv \begin{cases} A[l, :] & l \neq j \ A[i, :] & l = j \ \end{cases} \end{aligned} $$

Since $Z$ differs from $A$ only in the $j$th row, we must have that $Z'[k, j] = A'[k, j]$, since $Z'[k, j]$ depends on what happens on all rows and columns outside of $j$.

If we compute $det(Z)$ by expanding along the $j$ row, we get:

$$ \begin{aligned} &det(Z) = (-1)^{j+k} Z[j, k] det(Z'[k, j]) \ &det(Z) = (-1)^{j+k} A[j, k] det(Z'[k, j]) \ &det(Z) = (-1)^{j+k} A[j, k] det(A'[k, j]) \ &= D[i, j] \end{aligned} $$

But $Z$ has a repeated row: $A[j, :] = A[i, :]$ and $i \neq j$. Hence, $det(Z) = 0$. So, $D[i, j] = 0$ when $i \neq j$.

Hence, this means that $A adj(A) = det(A) I$.

• We can rapidly derive other properties from this reuation. For example, $det(A adj(A)) = det(det(A) I) = det(A)^n$, and hence $det(A) det(adj(A)) = det(A)^n$, or $det(adj(A)) = det(A)^{n-1}$.
• Also, by rearranging, if $det(A) \neq 0$, we get $A adj(A) = det(A) I$, hence $A (adj(A)/det(A)) = I$, or $adj(A)/det(A) = A^{-1}$.

Determinant in terms of exterior algebra

For a vector space $V$ of dimension $n$, Given a linear map $T: V \rightarrow V$, define a map $\Lambda T: \Lambda^n V \rightarrow \Lambda^n V$ such that $\Lambda T(v_1 \wedge v_2 \dots \wedge v_n) \equiv T v_1 \wedge T v_2 \dots \wedge T v_n$. Since the space $\Lambda^n V$ is one dimension, we will need one scalar $k$ to define $T$: $T(v_1 \wedge \dots \wedge v_n) = k v_1 \wedge \dots \wedge v_n$. It is either a theorem or a definition (depending on how one starts this process) that $k = det(T)$.

If we choose this as a definition, then let's try to compute the value. Pick orthonormal basis $v[i]$. Let $w[i] \equiv T v[i]$ (to write $T$ as a matrix). Define the $T$ matrix to be defined by the equation $w[i] = T[i][j] v[j]$. If we now evaluate $\Lambda_T$, we get:

$$ \begin{aligned} \Lambda T(v_1 \wedge \dots v_n) \ &= T(v_1) \wedge T(v_2) \dots \wedge T(v_n) \ &= w_1 \wedge w_2 \dots w_n \ &= (T[1][j_1] v[j_1]) \wedge (T[1][j_2] v[j_2]) \wedge (T[1][j_n] v[j_n]) \ &= (\sum_{\sigma \in S_n} (\prod_i T[i][\sigma(i)] sgn(\sigma)) v[1] \wedge v[2] \dots \wedge v_n \end{aligned} $$

Where the last equality is because:

• (1) Repeated vectors get cancelled, so we must have unique $v[1], v[2], \dots v[n]$ in the terms we collect. So all the $j_k$ must be distinct in a given term.
• A wedge of the form $T[1][j_1] v[j_1] \wedge T[2][j_2] v[j_2] \dots T[n][j_n] v[j_n]$, where all the $j_i$ are distinct (see (1)) can be rearranged by a permutation that sends $v_{j_i} \mapsto v_i$. Formally, apply the permutation $\tau(j_i) \equiv i$. This will reorganize the wedge into $T[1][j_1] T[2][j_2] \dots T[n][j_n] v[1] \wedge v[2] \wedge v[3] \dots v[n] (-1)^{sgn(\tau)}$, where the sign term is picked up by the rearrangement.
• Now, write the indexing into $T[i][j_i]$ in terms of a permutation $\sigma(i) \equiv j_i$. This becomes $\prod_i T[i][\sigma(i)] (-1)^{sgn(\tau)} v[1] \wedge v[2] \dots \wedge v[n]$.
• We have two permutations $\sigma, \tau$ in the formula. But we notice that $\sigma = \tau^{-1}$, and hence $sgn(\sigma) = sgn(\tau)$, so we can write the above as $\prod_i T[i][\sigma(i)] (-1)^{sgn(\sigma)} v[1] \wedge v[2] \dots \wedge v[n]$.
• Thus, we have recovered the "classical determinant formula".

Laplace expansion of determinant

From the above algebraic encoding of the determinant of $T[i][j]$ as $\sum_{\sigma \in S_n}sgn(\sigma)\prod_i T[i][\sigma(i)]$, we can recover the "laplace expansion" rule, that asks to pick a row $r$, and then compute the expression: as

$$ L_r(T) \equiv \sum_c T[r, c] (-1)^{r+c} det(T'(r, c)) $$

Where $T'(r, c)$ is the matrix $T$ with row $r$ and column $c$ deleted. I'll derive this concretely using the determinant definition for the 3 by 3 case. The general case follows immediately. I prefer being explicit in a small case as it lets me see what's going on.

Let's pick a basis for $V$, called $b[1], b[2], b[3]$. We have the relationship $v[i] \equiv Tb[i]$. We want to evaluate the coefficient of $v[1] \wedge v[2] \wedge v[3]$. First grab a basis expansion of $v[i]$ as $v[i] = c[i][j] b[j]$. These uniquely define the coefficients $c[i][j]$. Next, expand the wedge:

$$ \begin{aligned} & v[1] \wedge v[2] \wedge v[3] \ &= (c[1][1]b[1] + c[1][2]b[2] + c[1][3]b[3]) \wedge (c[2][1]b[1] + c[2][2]b[2] + c[2][3]b[3]) \wedge (c[3][1]b[1] + c[3][2]b[2] + c[3][3]b[3]) \end{aligned} $$

I now expand out only the first wedge, leaving terms of the form $c[1][1]b[1] (\cdot) + c[1][2]b2 c[1][3]b[3] (\cdot)$. (This corresponds to "expanding along and deleting the row" in a laplace expansion when finding the determinant) Let's identify the $(\cdot)$ and see what remains:

$$ \begin{aligned} & v[1] \wedge v[2] \wedge v[3] \ &= c[1][1]b[1] \wedge (c[2][1]b[1] + c[2][2]b[2] + c[2][3]b[3]) \wedge (c[3][1]b[1] + c[3][2]b[2] + c[3][3]b[3])

• c[1][2]b[2] \wedge(c[2][1]b[1] + c[2][2]b[2] + c[2][3]b[3]) \wedge(c[3][1]b[1] + c[3][2]b[2] + c[3][3]b[3])
• c[1][3]b[2] \wedge(c[2][1]b[1] + c[2][2]b[2] + c[2][3]b[3]) \wedge(c[3][1]b[1] + c[3][2]b[2] + c[3][3]b[3]) \end{aligned} $$

Now, for example, in the first term $c[1][1]b[1] \wedge (\cdot)$, we lose anything inside that contains a $b[1]$, as the wedge will give us $b[1] \wedge b[1] = 0$ (this corresponds to "deleting the column" when considering the submatrix). Similar considerations have us remove all terms that contain $b[2]$ in the brackets of $c[1][2]b[2]$, and terms that contain $b[3]$ in the brackets of $c[1][3]b[3]$. This leaves us with:

$$ \begin{aligned} & v[1] \wedge v[2] \wedge v[3] \ &= c[1][1]b[1] \wedge (c[2][2]b[2] + c[2][3]b[3]) \wedge (c[3][2]b[2] + c[3][3]b[3])

• c[1][2]b[2] \wedge(c[2][1]b[1] + c[2][3]b[3]) \wedge(c[3][1]b[1] + c[3][3]b[3])
• c[1][3]b[2] \wedge(c[2][1]b[1] + c[2][2]b[2] ) \wedge(c[3][1]b[1] + c[3][2]b[2]) \end{aligned} $$

We are now left with calculating terms like $(c[2][2]b[2] + c[2][3]b[3]) \wedge (c[3][2]b[2] + c[3][3]b[3])$ which we can solve by recursion (that is the determinant of the 2x2 submatrix). So if we now write the "by recursion" terms down, we will get something like:

$$ \begin{aligned} & v[1] \wedge v[2] \wedge v[3] \ &= c[1][1]b[1] \wedge (k[1] b[2] \wedge b[3])

• c[1][2]b[2] \wedge(k[2] b[1] \wedge b[3])
• c[1][3]b[2] \wedge(k[3] b[1] \wedge b[2]) \end{aligned} $$

Where the $k[i]$ are the values produced by the recursion, and we assume that the recursion will give us the coefficients of the wedges "in order": so we always have $b[2] \wedge b[3]$ for example, not $b[3] \wedge b[2]$. So, we need to ensure that the final answer we spit out corresponds to $b[1] \wedge b[2] \wedge b[3]$. If we simplify the current step we are at, we will get:

$$ \begin{aligned} & v[1] \wedge v[2] \wedge v[3] \ &= k[1] c[1][1]b[1] \wedge b[2] \wedge b[3]

• k[2] c[1][2]b[2] \wedge b[1] \wedge b[3]
• k[3] c[1][3]b[2] \wedge b[1] \wedge b[2] \end{aligned} $$

We need to rearrange our terms to get $b[1] \wedge b[2] \wedge b[3]$ times some constant. On rearranging each term into the standard form $b[1] \wedge b[2] \wedge b[3]$, we are forced to pick up the correct sign factors:

$$ \begin{aligned} & v[1] \wedge v[2] \wedge v[3] \ &= k[1] c[1][1]b[1] \wedge b[2] \wedge b[3] -k[2] c[1][2]b[1] \wedge b[2] \wedge b[3]

• k[3] c[1][3]b[1] \wedge b[2] \wedge b[3] \ &= (c[1][1]k[1] - c[1][2]k[2] + c[1][3]k[3])(b[1] \wedge b[2] \wedge b[3]) \end{aligned} $$

We clearly see that for each $c[i]$, the factor is $(-1)^i k[i]$ where $k[i]$ is the answer gotten by computing the determinant of the sub-expression where we delete the vector $b[i]$ (ignore the column) and also ignore the entire "row", by not thinking about $cj$ where $j \neq i$. So, this proves the laplace expansion by exterior algebra.

Deriving Cayley Hamilton for rings from $\mathbb Z$

I'll show the idea of how to prove Cayley Hamilton for an arbitrary commutative ring $R$ given we know Cayley Hamilton for $\mathbb Z$. I describe it for 2x2 matrices. The general version is immediate from this. Pick a variable matrix and write down the expression for the characteristic polynomial So if:

M = [a b]
    [c d]

then the characteristic polynomial is:

ch
= |M - xI|
=
|a-x b|
|c   d-x|

that's $ch(a, b, c, d, x) \equiv (a-x)(d-x) - bc = x^2 +x (a + d) + ad - bc$. This equation has $a, b, c, d, x \in R$ for some commutative ring $R$. Now, we know that if we set $x = M$, this equation will be satisfied. But what does it mean to set $x = A$? Well, we need to let $x$ be an arbitrary matrix:

x = [p q]
    [r s]

And thus we compute x^2 to be:

x^2 
= [p q][p q]
  [r s][r s]
= [p^2 + qr; pq + qs]
  [rp + sr; rq + s^2]

So now expanding out $ch(a, b, c, d, x)$ in terms of $x$ on substituting for $x$ the matrix we get the system:

[p^2 + qr; pq + qs] + (a + d) [p q] + (ad - bc)[1 0] = [0 0]
[rp + sr; rq + s^2]           [r s]            [0 1]   [0 0]

We know that these equations hold when $x = M$, because the Cayley-Hamilton theorem tells us that $ch(M) = 0$! So we get a different system with p = a, q = b, r = c, s = d, still with four equations, that we know is equal to zero! This means we have four intederminates a, b, c, d and four equations, and we know that these equations are true for all $\mathbb Z$. But if a polynomial vanishes on infinitely many points, it must identically be zero. Thus, this means that ch(A) is the zero polynomial, or ch(A) = 0 for all R. This seems to depend on the fact that the ring is infinite, because otherwise imagine we send $\mathbb Z$ to $Z/10Z$. Since we don't have an infinite number of $\mathbb Z$ elements, why should the polynomial be zero? I imagine that this needs zariski like arguments to be handled.

Cramer's rules

We can get cramer's rule using some handwavy manipulation or rigorizing the manipulation using geometric algebra.

Say we have a system of equations:

$$ \begin{aligned} a[1] x + b[1] y = c[1] \ a[2] x + b[2] y = c[2] \end{aligned} $$

We can write this as:

$$ \vec a x + \vec b y = \vec c $$

where $\vec a \equiv (a_1, a_2)$ and so on. To solve the system, we wedge with $\vec a$ and $\vec b$:

$$ \begin{aligned} \vec a \wedge (\vec a x + \vec b y) = \vec a \wedge \vec c \ \vec a \wedge \vec b y = \vec a \wedge \vec c \ y = \frac{\vec a \wedge \vec c}{\vec a \wedge \vec b} \ y = \frac{\begin{vmatrix} a[1] & a[2] \ c[1] & c[2] \end{vmatrix}}{ \begin{vmatrix} a[1] & b[1] \ a[2] & b[2] \end{vmatrix} } \end{aligned} $$

Which is exactly cramer's rule.

The formula for the adjugate matrix from Cramer's rule (TODO)

References

• More abstract proof of Cayley Hamilton
• PlanetMath: proof of Cayley Hamilton for commutative rings

Nakayama's lemma (WIP)

Geometric applications of Jacobson radical

vector fields over the 2 sphere (WIP)

We assume that we already know the hairy ball theorem, which states that no continuous vector field on $S^2$ exists that is nowhere vanishing. Using this, we wish to deduce (1) that the module of vector fields over $S^2$ is not free, and an explicit version of what the Serre Swan theorem tells us, that this module is projective

1. Vector fields over the 2-sphere is projective

Embed the 2-sphere as a subset of $\mathbb R^3$. So at each point, we have a tangent plane, and a normal vector that is perpendicular to the sphere: for the point $p \in S^2$, we have the vector $p$ as being normal to $T_p S^2$ at $p$. So the normal bundle is of the form:

$$ \mathfrak N \equiv { { s } \times { \lambda s : \lambda in \mathbb R } : s \in \mathbb S^2 } $$

• If we think of the trivial bundle, that is of the form $Tr \equiv { s } \times \mathbb R : s \in \mathbb S^2 }$.
• We want to show an isomorphism between $N$ and $T$.
• Consider a map $f: N \rightarrow Tr$ such that $f((s, n)) \equiv (s, ||n||)$. The inverse is $g: Tr \rightarrow N$ given by $g((s, r)) \equiv (s, r \cdot s)$. It's easy to check that these are inverses, so we at least have a bijection.
• To show that it's a vector bundle morphism, TODO.
• (This is hopelessly broken, I can't treat the bundle as a product. I can locally I guess by taking charts; I'm not sure how I ought to treat it globally!)

1. Vector fields over the sphere is not free

• 1. Given two bundles $E, F$ over any manifold $M$, a module isomorphism $f: \mathfrak X(E) \rightarrow \mathfrak X(F)$ of vector fields as $C^\infty(M)$ modules is induced by a smooth isomorphism of vector bundles $F: E \rightarrow F$.
• 2. The module $\mathfrak X(M)$ is finitely generated as a $C^\infty$ module over $M$.
• Now, assume that $\mathfrak X(S^2)$ is a free module, so we get that $\mathfrak X(S^2) \simeq \oplus_i C^\infty(S^2)$.
• By (2), we know that this must be a finite direct sum for some finite $N$: $mathfrak X(S^2) = \oplus_i=1^N C^\infty(S^n)$.
• But having $N$ different independent non-vanishing functions on $\mathbb S^2$ is the same as clubbing them all together into a vector of $N$ values at each point at $S^2$.
• So we get a smooth function $S^2 \rightarrow \mathbb R^n$, AKA a section of the trivial bundle $\underline{\mathbb R^n} \equiv S^2 \times \mathbb R^n$.
• This means that we have managed to trivialize the vector bundle over the sphere if vector fields over $S^2$ were a free module.
• Now, pick the element $S^2 \times { (1, 1, 1, 1, \dots) } \in S^2 \times \mathbb R^n$. This is a nowhere vanishing vector field over $S^2$. But such an object cannot exist, and hence vector fields over the sphere cannot be free.

References

• Smooth vector fields over $S^2$ is not a free module
• Smooth vector fields over $S^2$ is a projective module

Learning to talk with your hands

I was intruged by this HN thread about learning to talk with your hands. I guess I'm going to try and do this more often now.

Lovecraftisms

I recently binged a lot of Lovecraftian horror to get a sense of his writing style. Here's a big list of my favourite quotes:

His madness held no affinity to any sort recorded in even the latest and most exhaustive of treatises, and was conjoined to a mental force which would have made him a genius or a leader had it not been twisted into strange and grotesque forms.

seething vortex of time

Snatches of what I read and wrote would linger in my memory. There were horrible annals of other worlds and other universes, and of stirrings of formless life outside of all universes

clinging pathetically to the cold planet and burrowing to its horror-filled core, before the utter end.

appalled at the measureless age of the fragments

fitted darkly into certain Papuan and Polynesian legends of infinite antiquity

The condition and scattering of the blocks told mutely of vertiginous cycles of time and geologic upheavals of cosmic savagery.

uttermost horrors of the aeon-old legendry

The moon, slightly past full, shone from a clear sky, and drenched the ancient sands with a white, leprous radiance which seemed to me somehow infinitely evil.

with the bloated, fungoid moon sinking in the west

how preserved through aeons of geologic convulsion I could not then and cannot now even attempt to guess.

gently bred families of the town

could not escape the sensation of being watched from ambush on every hand by sly, staring eyes that never shut.

and there was that constant, terrifying impression of other sounds--perhaps from regions beyond life--trembling on the very brink of audibility.

little garden oasis of village-like antiquity where huge, friendly cats sunned themselves atop a convenient shed.

Better it be left alone for the years to topple, lest things be stirred that ought to rest forevrr in the black abyss

It clearly belonged to some settled technique of infinite maturity and perfection, yet that technique was utterly remote from any--Eastern or Western, ancient or modern--which I had ever heard of or seen exemplified. It was as if the workmanship were that of another planet.

intricate arabesques roused into a kind of ophidian animation.

never was an organic brain nearer to utter annihilation in the chaos that transcends form and force and symmetry.

away outside the galaxy and possibly beyond the last curved rim of space.

It was like the drone of some loathsome, gigantic insect ponderously shaped into the articulate speech of an alien species

In time the ruts of custom and economic interest became so deeply cut in approved places that there was no longer any reason for going outside them, and the haunted hills were left deserted by accident rather than by design

There were, too, certain caves of problematical depth in the sides of the hills; with mouths closed by boulders in a manner scarcely accidental, and with more than an average quota of the queer prints leading both toward and away from them

he fortified himself with the mass lore of cryptography

As before, the sides of the road showed a bruising indicative of the blasphemously stupendous bulk of the horror

The dogs slavered and crouched close to the feet of the fear-numbed family.

an added element of furtiveness in the clouded brain which subtly transformed him from an object to a subject of fear

fireflies come out in abnormal profusion to dance to the raucous, creepily insistent rhythms of stridently piping bull-frogs.

a seemingly limitless legion of whippoorwills that cried their endless message in repetitions timed diabolically to the wheezing gasps of the dying man

pandemoniac cachinnation which filled all the countryside

the left-hand one of which, in the Latin version, contained such monstrous threats to the peace and sanity of the world

Their arrangement was odd, and seemed to follow the symmetries of some cosmic geometry unknown to earth or the solar system

faint miasmal odour which clings about houses that have stood too long

I do not believe I would like to visit that country by night--at least not when the sinister stars are out

there was much breathless talk of new elements, bizarre optical properties, and other things which puzzled men of science are wont to say when faced by the unknown..

stealthy bitterness and sickishness, so that even the smallest bites induced a lasting disgust

plants of that kind ought never to sprout in a healthy world.

everywhere were those hectic and prismatic variants of some diseased, underlying primary tone without a place among the known tints of earth.

In her raving there was not a single specific noun, but only verbs and pronouns..

great bare trees clawing up at the grey November sky with a studied malevolence

There are things which cannot be mentioned, and what is done in common humanity is sometimes cruelly judged by the law.

monstrous constellation of unnatural light, like a glutted swarm of corpse-fed fireflies dancing hellish sarabands over an accursed marsh,

No traveler has ever escaped a sense of strangeness in those deep ravines, and artists shiver as they paint thick woods whose mystery is as much of the spirits as of the eye.

We live on a placid island of ignorance in the midst of black seas of infinity, and it was not meant that we should voyage far. The sciences, each straining in its own direction, have hitherto harmed us little; but some day the piecing together of dissociated knowledge will open up such terrifying vistas of reality, and of our frightful position therein, that we shall either go mad from the revelation...

form which only a diseased fancy could conceive

... dreams are older than brooding Tyre, or the contemplative Sphinx, or garden-girdled Babylon

iridescent flecks and striations resembled nothing familiar to geology or mineralogy.

miserable huddle of hut

Only poetry or madness could do justice to the noises heard by Legrasse's men as they ploughed on through the black morass.

In his house at R'lyeh dead Cthulhu waits dreaming

all the earth would flame with a holocaust of ecstasy and freedom.

The aperture was black with a darkness almost material.

Hairy ball theorem from Sperner's Lemma (WIP)

• Let $\Delta$ be an n-dimensional simplex with vertices $v_0, v_1, \dots, v_n$.
• Let $\Delta_i$ be the face opposite to vertex $v_i$. That is, $\Delta_i$ is the face with all vertices except $v_i$.
• The boundary $\partial \Delta$ is the union of all the $n+1$ faces of $\Delta_i$ (i is from $0$ to $n$).
• Let $\Delta$ be subdivided into smaller simplicies forming a simplciial complex $S$.
• Sperner's lemma: Let the vertices of $S$ be labelled by $\phi: S \rightarrow \Delta$ (that is, it maps all vertices of the simplicial complex $S$ to one of the vertices of the simplex $\Delta$), such that $v \in \Delta_i \implies \phi(v) \neq i$. Then there is at least one $n$-dimensional simplices of $S$ whose image is $\Delta$ (That is, there is at least one n-dimensional-sub-simplex $T \subseteq S$ such that vertices of $T$ are mapped to ${0, 1, \dots, n}$). More strongly, the number of such sub-simplices is odd.
• We can see that the map $\phi$ looks like some sort of retract that maps the complex $S$ to its boundary $\Delta$. Then Sperner's lemma tells us that there is one "region" $T \subseteq S$ that gets mapped onto $\Delta$.

1D proof of Sperner's: Proof by cohomology

• For 1D, assume we have a line with vertex set $V$ and edges $E$. Let the vertex at the beginning be $v_0$ and the vertx at the end be $v_1$. That is, $\Delta \equiv {v_0, v_1}$ and $S \equiv (V, E)$ is a subcomplex of $\Delta$ --- that is, it subdivides the line $\Delta$ into smaller portions. Let $\phi: S \rightarrow \Delta$ be the labelling function.

• create a function $f: \Delta \rightarrow \mathbb F_2$ that assigns $0$ to $v_0$ and $+1$ to $v_1$: $f(v_0) \equiv 0; f(v_1) \equiv 1$. Use this to generate a function on the full complex $F: S \rightarrow F_2; F(v) \equiv F(\phi(v))$.

• From $F$, generate a function on the edges $dF: E \rightarrow F_2; dF(\overline{vw}) = F(w) + F(v)$. See that this scores such that $dF(AB) = +1$, $dF(BA) = +1$, $dF(AA) = dF(BB) = 0$. (Recall that the arithmetic is over $F_2$) So, $dF$ adds a one every time we switch from $A$ to $B$ or from $B$ to $A$.

• However, we also see that $dF$ is generated from a "potential function "f". Hence we have the identity $\sum_{e \in E} dF(e) = f(v_1) - f(v_0) = 1 - 0 = 1$. Hence, we must have switched signs an odd number of times.

• Since we start from $A$, that means we must have switched from $A$ to $B$ an odd number of times.

2D proof of Sperner's: Proof by search

• Start from an edge in the bottom $ef$ labeled $BC$. We are looking for a simplex labeled $ABC$.
• To start: Pick some vertex above $ef$, say $g$. If this is labeled $A$, we are done. If not, say this is labeled $B$. So we get triangle $efg=ABB$. Launch our search procedure from this triangle $efb$.
• Find the triangle adjacent to $efg$ along the edge $eg=AB$ (the other $AB$ edge, not the one we started with). If this adjacent triangle $egh$ has $h=A$ we are done. If not, move to the triangle $egh$.
• See that we will either find a triangle labeled $ABC$, or we will keep running into triangles labeled $ABB$.
• We cannot ever repeat a triangle in our path; to repeat a triangle is to start with some edge $xy$ and then to pick a vertex $z$ such that $xyz=efg$ where $efg$ was already picked. This must mean that the edge $ef$ was already picked. [WIP]

Proof of hairy ball by sperner's lemma [WIP]

Why hairy ball is interesting: Projective modules

The reason I care about the hairy ball theorem has to do with vector fields. The idea is to first think of smooth vector fields over a smooth manifold. What algebraic structure do they have? Indeed, they are a vector space over $\mathbb R$. However, it is difficult to exhibit a basis. Naively, for each point $p \in M$, we would need a basis $T_p B \subset T_p M$ as a basis. This brings in issues of smoothness, etc. Regardless, it would be uncountable in dimension.

On the other hand, let's say we allow ourselves to consider vector fields as modules over the ring of smooth functions on a manifold. That is, we can scale the vector field by a different value at each point.

We can hope the ""dimension"" of the module is much smaller. So, for example, if we think of $\mathbb R^2$, given some vector field $V \equiv v_x \hat x + v_y \hat y$, the functions $v_x$ and $v_y$ allow us to write basis! Create the vector fields $V_x \equiv \hat x$ and $V_y \equiv \hat y$. Then any vector field $V$ can be written as $V = v_x V_x + v_y V_y$ for functions $v_x, v_y$ in a unique way!

However, as we know, not all modules are free. A geometric example of such a phenomenon is the module of vector fields on the sphere. By the hairy ball theorem, any vector field must vanish at at least a single point. So if we try to build a vector field pointing "rightwards" (analogous to $\hat x$) and "upwards" (analogous $\hat y$), these will not be valid smooth vector fields, because they don't vanish! So, we will be forced to take more than two vector fields. But when we do that, we will lose uniqueness of representation. However, all is not lost. The Serre Swan theorem tells us that any such module of vector fields will be a projective module. The sphere gives us a module that is not free. I'm not sure how to show that it's projective.

Simple example of projective module that is not free.

• Let $K$ be a field. Consider $R \equiv K \times K$ as a ring, and let $M \equiv K$ be a module on top of $R$.

• $M$ is a projective module because $M \oplus K \simeq R$ (that is, we can direct sum something onto it to get the some $\oplus_i R$)

• On the other hand, $M$ itself is not free because $M \neq \oplus_i R$ for any $i$. Intuitively, $M$ is "half an $R$" as $M \simeq K$ while $R \simeq K\times K$.

• The geometric picture is that we have a space with two points ${p, q}$. We have a bundle on top of it, with $M$ sitting on $p$ and $0$ (the trivial module) sitting on top of $q$. When we restrict to $p$, we have a good bundle $M$.

• But in total over thr space, we can't write the bundle as $M \times {p, q}$ because the fibers have different dimensions! The dimension over $p$ is $dim(M) = 1$ while over $q$ is $dim(0) = 0$.

• What we can do is to "complete" the bundle by adding a copy of $M$ over $q$, so that we can then trivialise the bundle to write $M \times {p, q}$.

• So, a projective module corresponds to a vector bundle because it locally is like a vector space, but may not be trivialisable due to a difference in dimension, or compatibility, or some such.

• Sperner's lemma, Brower's fixed point theorem, and cohomology

CS and type theory: Talks by vovodesky

• Talk 1: Computer Science and Homotopy Theory
• Think of ZFC sets as rooted trees. Have two axioms:
• (1) all branches of all vertices are non-isomorphic (otherwise a set would have two copies of the same element)
• (2) Each leaf must be at finite depth from the root.
• This is horrible to work with, so type theory!
• Talk 2: What if foundations of math is inconsistent?
• We "know" that first order math is consistent. We can prove that it is impossible to prove that first order math is consistent!
• Choice 1: If we "know" FOL is consistent, then we should be able to transform this knowledge into a proof, then 2nd incompleteness is false.
• Choice 2: Admit "transcendental" part of math, write dubious philosophy.
• Choice 3: Admit that our sensation that FOL +arithmetic is consistent is an illusion and admit that FOL arithmetic is inconsistent.
• Time to consider Choice 3 seriously?

First order arithmetic

Mathematical object which belongs to class of objects called formal theories. Has four pieces of data:

1. Special symbols, names of variables.
2. Syntactic rules.
3. Deduction rules: Construct new closed formulas from old closed formula.
4. Axioms: collection of closed formulas.

Anything that is obtainable from these deduction rules is called a theorem. First order logic have symbols: ∀, ∃, ⇒, !(not) and so on. First order theory is inconsistent if there a closed formula $A$ such that both $A$ and $!A$ is a theorem.

• Free variables describe subsets. Eg: ∃ n: n^2 = m describes the set { m : ∃ n: n^2 = m }.
• It's possible to construct subsets (formulae with one free variable) whose membership is undedicable. So you can prove that it is impossible to say anything whatsoever about these subsets.

Gentzen's proof and problems with it

Tries to reason about trees of deduction. Show that proofs correspond to combinatorial objects. Show that inconsistency corresponds to an infinite decreasing sequence that never terminates. Then he says that it is "self evident" that this cannot happen. But it is not self evident!

What would inconsistency of FOL mean for mathematicians?

• Inconsistency of FOL implies inconsistency of many other systems (eg. set theory).
• Inconsistency of FOL implies inconsistency of constructive (intuitionistic) mathematics! (WTF?) shown by Godel in 1933. Takes a proof of contradiction in classical and strips off LEM.
• We need foundations that can create reliable proofs despite being inconsistent!
• Have systems that react to inconsistency in less drastic ways. One possible candidate is constructive type theories. A proof of a formula in such a system is itself a formula in the system. There are no deduction rules, only syntactic rules. So a proof is an object that can be studied in the system. If one has a proof of contradiction, then such a proof can be detected --- they have certain properties that can be detected by an algorithm (what properties?)

New workflow

• Formalize a problem.
• Construct creative solution.
• Submit proof to a "reliable" verifier. If the verifier terminates, we are done. If the verifier does not terminate, we need to look for other proofs that can terminate.
• our abstract thinking cancels out by normalisation :P

Summary

• Correct interpretation of 2nd incompleteness is a step of proof of inconsistency of FOL (Conjecture).
• In math, we need to learn how to use inconsistent theories to obtain reliable proofs. Can lead to more freedom in mathematical workflow.

Univalent Foundations: New Foundations of Mathematics

• Talk 3: Univalent foundations --- New Foundations of Mathematics

• Was uncertain about future when working on 2-categories and higher math. No way to ground oneself by doing "computations" (numerical experiments). To make it worse, the existing foundations of set theory is bad for these types of objects.

• Selected papers on Automath.

• Overcoming category theory as new foundations was very difficult for vovodesky.

• Categories are "higher dimensional sets"? NO! Categories are "posets in the next dimension". Correct version of "sets in the next dimension" are groupoids (WHY?) MathOverflow question

• Grothendeick went from isomorphisms to all morphisms, this prevented him from gravitating towards groupoids.

• Univalent foundations is a complete foundational system.

• Sets are groupoids on the next dimension

Vovodesky's univalence principle --- Joyal

• Talk 5: Vovodesky's univalence principle --- Joyal

• Univanent type theory is arrived at by adding univalence to MLTT.

• Goal of univalent foundations is to apply UTT to foundations.

• Univalence is to type theory what induction principle is to peano arithmetic

• Univalence implies descent. Descent implies Blakers Massey-theorem, which implies Goodwille calculus.

• The syntactic system of type theory is a tribe.

• A clan is a category equipped with a class of carrable maps called fibrations. A map is carrable if we can pull it back along any other map.

• A clan is a category along with maps called "fibrations", such that (1) every isomorphism is a fibration, (1) closed under composition, (3) fibrations are carrable, (4) base change of fibration is a fibration, (4) Category has a terminal object, and map into the terminal object is a fibration.

• A map $u: A \rightarrow B$ is anodyne if it does something good with respect to fibrations.

• A tribe is a clan such that (1) base chnge of anodyne along fibration is anodyne, (2) every map factorizes as anodyne followed by fibration.

• Kan complexes form a tribe. A fibration is a Kan fibration. A map is anodyne here if it is a monomorphism and a homotopy equivalence.

• Given a tribe $E$, can build a new tribe by slicing $E/A$ (this is apparently very similar to things people do in Quillen Model categories).

• A tribe is like a commutative ring. We can extend by adding new variables to get polynomial rings. An elementary extension is extending the tribe by adding a new element.

• If $E$ is a tribe, an object of $E$ is a type. We write E |- A : Type.

• If we have a map $a: 1 -> A$, we regard this as an element of A: E |- a : A.

• A fibration is a family of objects. This is a dependent type x : A |- E(x): Type. E(x) is the fiber of p: E -> A at a variable element x : A.

• A section of a fibration gives an element of the fibration. We write this as x : A |- s(x) : E(x). s(x) denotes the value of s: A -> E of a variable element x : A. (Inhabitance is being able to take the section of a fiber bundle?!)

• change of parameters / homomorphism is substitution.

y : B |- E(y) : Type
--------------------
x : A |- E(f(x)) : Type

This is pulling back along fibrations.

• Elementary extension E -> E(A) are called as context extensions.

|- B : Type
-----------
x : A |- B : Type

• A map between types is a variable element f(x) : B indexed by x : A

x : A |- f(x) : B

• Sigma formation rule: The total space of the union is the sum of all fibers(?)

x: A |- E(x): Type
------------------
|- \sum{x : A}E(x): Type

x: A |- E(x): Type
------------------
y : B |- \sum{x : f^{-1}(y)}E(x): Type

• Path object for $A$ is obtained by factorial diagonal map diag: a -> (a, a) as an anodyne map r: A -> PA followed by a fibration (s, t) : PA -> A x A.

• A homotopy h: f ~ g between two maps f, g : A -> B is a maph: A -> PB such that sh = f and th = g. homotopy is a congruence.

• x: A, y : A |- Id_A(x, y) : Type called the identity type of A.

• An element p: Id_A(x, y) is a proof that x =A y.

• Reflexivity term x : A |- r(x) : Id_A(x, x) which proves x =A x.

• The identity type is a path object

• $\gamma(x, y): Id_A(x, y) -> Eq(E(x), E(y))$. $\gamma$ is some kind of connection: given a path from $x$ to $y$, it lets us transport $E(x)$ to $E(y)$, where the $Eq$ is the distortion from the curvature?

Hilbert basis theorem for polynomial rings over fields (WIP)

Theorem: Every ideal $I$ of $k[x_1, \dots, x_n]$ is finitely generated.

First we need a lemma:

Lemma:

Let $I \subseteq k[x_1, \dots, x_n]$ be an ideal. (1) $(LT(I)) \equiv $ is a monomial ideal. An ideal $I$ is a monomial ideal if there is a subset $A \subseteq \mathbb Z^n_{\geq 0}$ (possibly infinite) such that $I = (x^a : a \in a)$. That is, $I$ is generated by monomials of the form $x^a$. Recall that since we have

Proof of hilbert basis theorem

• We wish to show that every ideal $I$ of $k[x_1, \dots, x_n]$ is finitely generated.
• If $I = { 0 }$ then take $I = (0)$ and we are done.
• Pick polynomials $g_i$ such that $(LT(I)) = (LT(g_1), LT(g_2), \dots, LT(g_t))$. This is always possible from our lemma. We claim that $I = (g_1, g_2, \dots, g_t)$.
• Since each $g_i \in I$, it is clear that $(g_1, \dots, g_t) \subseteq I$.
• Conversely, let $f \in I$ be a polynomial.
• Divide $f$ by $g_1, \dots, g_t$ to get $f = \sum_i a_i g_i + r$ where no term of $r$ is divisible by $LT(g_1), \dots, LT(g_t)$. We claim that $r = 0$.

References

• Cox, Little, O'Shea: computational AG.

Covering spaces (WIP)

Covering spaces: Intuition

• Consider the map $p(z) = z^2 : \mathbb C^\times \rightarrow \mathbb C^\times$. This is a 2-to-1 map. We can try to define an inverse regardless.
• We do define a "square root" if we want. Cut out a half-line $[0, -infty)$ called $B$ for branch cuts. We get two functions on $q_+, q_-: \mathbb C - B \rightarrow \mathbb C^\times$, such that $p(q_+(z)) = z$. Here, we have $q_- = - q_+$.
• The point of taking the branch cut is to preserve simply connectedness. $\mathbb C^\times$ is not simply connected, while $\mathbb C/B$ is simply connected! (This seems so crucial, why has no one told me this before?!)
• Eg 2: exponential. Pick $exp: \mathbb C \rightarrow \mathbb C^\times$. This is surjective, and infinite to 1. $e^{z + 2 \pi n} = e^{iz}$.
• Again, on $\mathbb C / B$, we have $q_n \equiv \log + 2 \pi i n$, such that $exp(q_n(z)) = z$.
• A covering map is, roughly speaking, something like the above. It's a map that's n-to-1, which has n local inverse defined on simply connected subsets of the target.
• So if we have $p: Y \rightarrow X$, we have $q: U \rightarrow Y$ (for $U \subseteq X$) such that $p(q(z)) = z, \forall z \in U$.

Covering spaces: Definition

• A subset $U \subset X$ is a called as an elementary neighbourhood if there is a discrete set $F$ and a homeomorphism $h: p^{-1}(U) \rightarrow U \times F$ such that $p|{p^{-1}(U)}(y) = fst(h)$ or $p|{p^{-1}(U)} = pr_1 \circ h$.
• Alternative definition A subset $U \subset X$ is called as evenly covered/elementary nbhd if $p^{-1}(U) = \sqcup \alpha V_\alpha$ where the $V_\alpha$ are disjoint and open, and $p|{V\alpha} : V_\alpha \rightarrow U$ is a homeomorphism for all $\alpha$.
• An elementary neighbourhood is the region where we have the local inverses (the complement of a branch cut).
• We get for each $i \in F$ , a map $q_i : U \rightarrow U \times F; q_i(x) = (x, i)$ and then along $h^{-1}$ sending $h^{-1}(x, i) \in p^{-1}(U)$.
• We say $p$ is a covering map if $X$ is covered by elementary neighbourhoods.
• We say $V \subseteq Y$ is an elementary sheet if it is path connected and $p(V)$ is an elementary neighbourhood.
• So, consider $p(x) = e^{ix}: \mathbb R \rightarrow S^1$. If we cut the space at $(0, 0)$, then we will have elementary neighbourhood $S^1 - {(0, 0)}$ and elementary sheets $(2 \pi k, 2 \pi+1)$.
• The point is that the inverse projection $p^{-1}$ takes $U$ to some object of the form $U \times F$: a local product! So even though the global covering space $\mathbb R$ does not look like a product of circles, it locally does. So it's some sort of fiber bundle?

Slogan: Covering space is locally disjoint copies of the original space.

Path lifting and Monodromy

• Monodromy is behaviour that's induced in the covering space, on moving in a loop in a base.
• Etymology: Mono --- single, drome --- running. So running in a single loop / running around a single time.
• Holonomy is a type of monodromy that occurs due to parallel transport in a loop, to detect curvature
• Loop on the base is an element of $\pi_1(X)$.
• Pick some point $x \in X$. Consider $F \equiv \pi^{-1}(x)$ ($F$ for fiber).
• Now move in a small loop on the base, $\gamma$. The local movement will cause movement of the elements of the fiber.
• Since $\gamma(1) = \gamma(0)$, the elements of the fiber at the end of the movement are equal to the original set $F$.
• So moving in a loop induces a permutation of the elements of the fiber $F$.
• Every element of $\pi_1(X)$ induces a permutation of elements of the fiber $F$.
• This lets us detect non-triviality of $\pi_1(X)$. The action of $\pi_1(X)$ on the fiber lets us "detect" what $\pi_1(X)$ is.
• We will define what is means to "move the fiber along the path".

Path lifting lemma

Theorem:Suppose $p: y \rightarrow X$ is a covering map. Let $\delta: [0, 1] \rightarrow X$ be a path such that $\delta(0) = x$, and let $y \in p^{-1}(x)$ [$y$ is in the fiber of $x$]. Then there is a unique path $\gamma: [0,1] \rightarrow Y$ which "lifts" $\delta$. That is, $\delta(p(y)) = \gamma(y)$, such that $\gamma(0) = Y$.

Slogan: Paths can be lifted. Given how to begin the lift, can be extended all the way.

• Let $N$ be a collection of elementary neighbourhoods of $X$.
• ${ \delta^{-1}(U) : U \in N }$ is an open cover (in the compactness sense) of $[0, 1]$.
• By compactness, find a finite subcover. Divide interval into subintervals $0 = t_0 < t_1 < \dots t_n = 1$ such that $\delta|k = \delta|{[t_k, t{k+1}]}$ lands in $U_k$, an elementary neighbourhood.
• Build $\gamma$ by induction on $k$.
• We know that $\gamma(0)$ should be $y$.
• Since we have an elementary neighbourhood, it means that there are a elementary sheets living over $U_0$, indexed by some discrete set $F$. $y$ lives in one of thse sheets. We have local inverses $q_m$. One of them lands on the sheet of $y$, call it $q$. So we get a map $q: U_0 \rightarrow Y$ such that $q(x) = y$.
• Define $\gamma(0) \equiv q(\delta(0)) = q(x) = y$.
• Extend $\gamma$ upto $t_1$.
• Continue all the way upto $t_k$.
• To get $\gamma$ from $(t_k, t_{k+1}$, there exists a $q_k: U_k \rightarrow Y$ such that $q_k(\delta(t_k)) = \gamma(t_k)$. Define $\gamma(t_k \leq t \leq t_{k_1}) \equiv q_k(\delta(t_k))$.
• This is continuous because $\delta$ continuous by definition, $q_k$ continuous by neighbourhood, $\gamma$ is pieced together such that endpoints fit, and is thus continuous.
• Can check this is a lift! We get $p \circ \gamma = p \circ q_k \circ \delta_k$. Since $q_k$ is a local inverse of $p$, we get $p \circ \gamma = \delta_k$ in the region.

7.03: Path lifting: uniqueness

If we have a space $X$ and a covering space $Y$, for a path $gamma$ that starts at $x$, we can find a path $\gamma'$ which starts at $y \in p^{-1}(x)$ and projects down to $\gamma$: $\gamma(t) = p(\gamma'(t))$. We want to show that this path lift is unique

Lemma

Let $p: Y \rightarrow X$ be a covering space. Let $T$ be a connected space Let $F: T \rightarrow X$ be a continuous map (for us, $T \simeq [0, 1]$). Let $F_1, F_2: T \rightarrow Y$ be lifts of $F$ ($p \circ F_1 = F$, $p \circ F_2 = F$). We will show that $F_1 = F_2$ iff the lifts are equal for some $t \in $T.

Slogan: Lifts of paths are unique: if they agree at one point, they agree at all points!

• We just need to show that if $F_1$ and $F_2$ agree somewhere in $Y$, they agree everywhere. It is clear that if they agree everywhere, they must agree somewhere.
• To show this, pick the set $S$ where $F_1, F_2$ agree in $Y$: $S \equiv { t \in T : F_1(t) = F_2(t) }$.
• We will show that $S$ is open and closed. Since $T$ is connected, $S$ must be either the full space or the empty set. Since $S$ is assumed to be non-empty, $S = T$ and the two functions agree everywhere.
• (Intuition: if both $S$ and $S^c$ are open, then we can build a function that colors $T = S \cup S^c$ in two colors continuously; ie, we can partition it continuously; ie the spaces must be disconnected. Since $T$ is connected, we cannot allow that to happen, hence $S = \emptyset$ or $S = T$.)
• Let $t \ in T$. Let $U$ be an evenly covered neighbourhood/elementary neighbourhood of $F(t)$ downstairs (in $X$). Then we have $p^{-1}(U) = \sqcup_\alpha V_\alpha$ such that $p|V{\alpha}: V\alpha \rightarrow U$ is a local homeomorphism.
• Since $F_1, F_2$ are continuous, we will have opens $V_1, V_2$ in $V_\alpha$, which contain $F_1(t), F_2(t)$ upstairs (mirrroring $U$ containing $F(t)$ downstairs).
• The pre-images of $V_1$, $V_2$ along $F_1, F_2$ give us open sets $t \in T_1, T_2 \subseteq T$.
• Define $T* = T_1 \cap T_2$. If $F_1(t) \neq F_2(t)$, then $V_1 \neq V_2$ and thus $F_1 \neq F_2$ on all of $T*$. So, $S^c = T*$ is open.
• If $F_1(t) = F_2(t)$, then $V_1 = V_2$ and thus $F_1 = F_2$ on $T*$ (since $p \circ F_1 = F = p \circ F_2$, and $p$ is injective within $U$, ie within $V_1, V_2$). So $S$ is open.
• Hence we are done, as $S$ is non-empty and clopen and is thus equal to $T$. Thus, the two functions agree on all of $T$.

Homotopy lifting, Monodromy

• Given a loop $\gamma$ in $X$ based at $x$ , the monodromy around $\gamma$ is a permutation $\sigma_\gamma : p^{-1}(x) \rightarrow p^{-1}(x)$, where $\sigma_{\gamma}(y) \equiv \gamma^y(1)$ where $\gamma^y$ is the unique lift of $\gamma$ staring at $y$. We have that $\sigma_{\gamma} \in Perm(p^{-1}(x))$.
• Claim: if $\gamma_1 \simeq \gamma_2$ then $\sigma_{\gamma_1} = \sigma_{\gamma_2}$.
• We need a tool: homotopy lifting lemma.

Slogan: permutation of monodromy depends only on homotopy type

Homotopy lifting lemma/property of covering spaces

Suppose $p: Y \rightarrow X$ is a covering map and $\gamma_s$ is a homotopy of paths rel. endpoints ($\gamma_s(0)$ and $\gamma_s(1)$ are independent of $s$ / endpoints are fixed throughout the homotopy). Then there exists for each lift $\gamma'_0 : [0, 1] \rightarrow Y$ of $\gamma_0:[0,1] \rightarrow X$ (ie, $p \circ \gamma'_0 = gamma_0$), a completion of the lifted homotopy $\gamma'_s: [0, 1] \rightarrow Y$ (ie, $p \circ gamma'_s = gamma_s$). Moreover, this lifted homotopy is rel endpoints: ie, the endpoints of $gamma'$ are independent of $s$.

Slogan: homotopy lifted at 0 can be lifted for all time

• Let $H: [0, 1] \times [0, 1] \rightarrow X$ be the homotopy in $X$ such that $H(s, t) = \gamma_s(t)$. Subdivide the square into rectangles $R_{ij}$ such that $H(R_{ij})$ is contained in $U_{ij}$ for some elementary neighbourhood $U_{ij}$. We build $H': [0, 1] \times [0, 1] \rightarrow Y$ by building local inverses $q_{ij} : U_{ij} \rightarrow Y$ such that $p \circ q_{ij} = R_{ij}$. We then set $H'|{R{ij}} = q_{ij} \circ H$.

• Reference video

• Notes for uniqueness of path lifting

Van Kampen theorem (WIP)

• Reference video

Wedge Sum and Smash Product

I sometimes forget which is which. I now remember this as folows:

• First, these work on based spaces so we always need to think of based points.
• Wedge is a sum, so it's going to be some type of union. It needs to identify things, so it better be $A \cup B / \sim$ where $\sim$ identifies based points.
• Smash is a product, so it's going to be some type of product. It needs to identify things, so it better be $A \times B / \sim$, where $\sim$ crushes together anything that has a based point. So $(*, a), (a, ), (, *)$ are all crushed.
• If we don't remember the "sum" and "product" bit, and only remember "wedge" and "smash", then "wedge" starts with a "w" which looks like \/so it should be a union.

Quotient topology

I watched this for shits and giggles. I don't know enough topology at all, but it's fun to watch arbitrary math videos.

Quotient topology: Defn, examples

• Intended to formalise identifications.

Given space $X$ and equivalence relation $\sim$ on $X$, the quotient set $X/\sim$ inherits a topology. Let $q : X \rightarrow X/\sim$ send point to equivalence class. Quotient topology is the most refined topology on $X/\sim$ such that $q$ is continuous. That is, it has the most open sets for which this map is continuous.

• More explicitly, a set $U \subset X/\sim$ (which is a collection of equivalence classes) is open iff $q^{-1}(U)$ is open in $X$.
• Even more explicitly, $V \subseteq X/\sim$ is open iff $U_V \equiv { x \in U : [x] \in V }$ is open in $X$.
• Even more explicitly, we can write $U \equiv \cup_{v \in V} v$, because the elements of $v$ are equivalence classes.

Claim: quotient topology is a topology

• The preimage of the empty set is the empty set, and thus is open.
• The preimage of all equivalence classes is the full space, and thus open.
• Preimage of union is union of preimages: $\cup_i q^{-1}(V_i)$ extend $h$ to get a new homotopy $H$: $H_0 = id_X$ and $H_t|A = h_t$.

$(X, A)$ have HEP and $A$ is contractible, then $X \simeq X/A$

• Pick $q: X \rightarrow X/A$. We need another map such that their compositions are homotopic to the identities of $X$ and $X/A$.
• Define $s: X/A \rightarrow X$ as a section of $q$, given by $s([a]) \equiv a, s([x]) \equiv x$. This is a section of $q$ since $q \circ s = id_{X/A}$ (That is, $s$ maps entirely within the fibers of $q$).
• Consider $s_t : H_t \circ s : X/A \rightarrow X$. That is, lift from $X/A$ to $X$ using $s$ and then perform $H_t$ on $X$. We claim that The map $(H_1 \circ s)$ is the homotopy inverse of $q$.
• (1a) $(H_1 \circ s) \circ q : X \rightarrow X$ is equal to $H_1$, as $H_1(s(q(A))) = H_1(s([a])) = H_1(a) = a = H_1(A)$, and $H_1(s(q(x))) = H_1(s([x])) = H_1(x)$.
• (1b) So we have $(H_1 \circ s) \circ q = H_1 \simeq H_0 = id_X$, as $H_0 = id_X$ is from defn, and $H_1 \simeq H_0$ is from homotopy. So we are done in this direction.
• (2a) Consider $q \circ (H_1 \circ s) : X \rightarrow X/A$. We wish to show that this is continuous. Let's show that it lifs to a continous map upstairs. So consider $q \circ (H_t \circ s) \circ q : X \rightarrow X/A$. We claim that this is equal to $q \circ H_t$, which is continuous as it is a composition of continuous maps.
• This relationship is hopefully intuitive: $q \circ (H_t \circ s) \circ q$ asks us to treat all of $A$ as if it were $a$ before applying $H_t$. Since $q$ kills whatever $H_t$ does after, and $H_t$ guarantees to keep $A$ within $A$, it's fine if we treat all of $A$ as just $a$. $q \circ H_t$ asks us to treat $A$ as $A$ itself, and not $a$. Since $q$ kills stuff anyway, we don't really care. The real crux of the argument is that $q \circ stab_A = q \circ stab_A \circ s \circ q$ where $stab_A$ is a map that stabilizes $A$.
• (2b) Consider $(q \circ (H_t \circ s) \circ q)(A) = (q \circ H_t \circ s)([a]) = (q \circ H_t)(a)$ --- Since $H_t(a) = h_t(a) = a' \in A$, we crush all data regardless of what happens. This is the same as the value $(q \circ H_t)(A) = [a]$ as $H_t(A) \subseteq A$ and $q(A) = [a]$. For the other set, we get $(q \circ (H_t \circ s) \circ q)(x) = q \circ H_t \circ s([x]) = q \circ H_t(x)$ and hence we are done.
• (2c) Now since $q \circ (H_t \circ s))$ is continuous, and that $q \circ (H_0 \circ s) : X/A \rightarrow X/A = id_{X/A}$, we are done since we can homotope from $q \circ H_1 \circ s \simeq q \circ H_0 \circ s = id_{X/A}$.
• (2d) TODO: We should be able to clean this proof up by refactoring $H_t$, $s$ and $q$ somehow to exploit their relationships.

Slogan: Use HEP to find homotopy $H$. Use $H_1 \circ s$ as inverse to quotient.

CW Complexes and HEP

If $X$ is a CW complex and $A$ is a closed subcomplex, then it has the HEP. A closed subcomplex is a union of closed cells of $X$ such that $X$ is obtained by adding more cells to $A$.

Lemma

If $e$ is a disk, then there is a continuous map from $e \times [0, 1]$ to $\partial e \times [0, 1] \cup (e \times { 0 })$.

Lemma

If $X$ is obtained from $A$ by attaching one $k$-cell, then $(X, A)$ has HEP.

Given a homotopy $h_t: A \times [0, 1] \rightarrow Y$ and a new homotopy $F_0: X \rightarrow Y$ such that $F_0|A = h_t$, we want to complete $F$ such that $F_t|A = h_t$.

The only part I don't know where to define $F$ on is the new added $e$ portion. So I need to construct $H$ on $e \times [0, 1]$. Use the previous map to get to $e \times [0, 1] \cup (e \times {0})$. This is in the domain of $F_0$ or $h_t$, and thus we are done.

CW Complexes have HEP

Induction on lemma. base case is empty set.

Connected 1D CW Complex

Theorem: any connected 1D CW complex is homotopic to wedge of circles.

• Find a contractible subcomplex $A$ of $X$ that passes through all $0$ cells.
• By HEP, $X \simeq X/A$. $X/A$ has only one zero-cell and other one cells. One cells are only attached to zero cells. Hence, is a wedge of circles.
• The idea to find a contractible subcomplex is to put a partial order on the set of all contractible cell complexes by inclusion.
• Pick a maximal element with respect to this partial order.
• Claim: maximal element must contain all zero cells. Suppose not. Then I can add the new zero cell into the maximal element (why does it remain contractible? Fishy!)

Stable homotopy theory

We like stable homotopy groups because of the Freudenthal suspension theorem which tells us that homotopy groups stabilise after many suspensions.

The basic idea seems to be something like a tensor-hom adjunction. We have the loop spaces which are like $S^1 \rightarrow X$ and the suspension which is like $S^1 \wedge X$. The theory begins by considering the tensor-hom-adjunction between these objects as fundamental.

• We then try to ask: how can one invert the suspension formally? One tries to do some sort of formal nonsense, by declaring that maps between $\Sigma^{-n}X$ and $\Sigma^{-m} Y$ , but this doesn't work due to some sort of grading issue.
• Instead, one repaces a single object $X$ with a family of objects ${ X_i }$ called as the spectrum. Then, we can invert the suspension by trying to invert maps between objects of the same index.

References

• Homotopy Extension
• CW complexes
• Stable homotopy theory 1

Tychonoff theorem (WIP)

Simply connected spaces

• A space is simply connected iff fundamental group at all points is trivial.
• We usually don't want to talk about basepoint, so we assume that the space is path-connected. This means we can move the basepoint around, or not take about the basepoint.
• So, a path-connected space is simply connected iff the fundamental group is trivial.

Simply connected => all paths between two points are homotopic.

If $x, y$ are two points, then there is a single unique homotopy class of points from $x$ to $y$. Consider two paths from $x$ to $y$ called $\alpha, \beta$. Since $\beta^{-1} \circ \alpha \in \pi_1(x, x) = 1$, we have that $\beta^{-1} \circ \alpha \simeq \epsilon_x$. [ie, path is homotopic to trivial path]. compose by $\beta$ on the left: This becomes $\alpha \simeq \beta$.

• This is pretty cool to be, because it shows that a simply connected space is forced to be path connected. Moreover, we can imagine a simply connected space as one we can "continuously crush into a single point".

Finitely generated as vector space v/s algebra:

• To be finitely generated as a vector space over $K$ from a generating set $S$ means that we take elements of the form $\sum_i k_i s_i$, or abbreviated, elements of the form $\sum KS$
• To be finitely generated as a $K$ algebra from a generating set $S$, we take elements of the form $\sum_i k_i s_i + \sum_{ij} k_{ij} s_i s_j + \dots$. To abbreviate, elements of the form $\sum C + CS + CS^2 + CS^3 \dots = C/(1-S)$.

As a trivial example, consider $K[X]$. This is not finitely generated as a vector space since it doesn't have a finite basis: the obvious choice of generating set ${ 1, X, X^2, \dots }$ is not finite. It is finitely generated as a $K$-algebra with generating set ${ X }$.

Weak and Strong Nullstllensatz

Weak Nulstellensatz: On the tin

For every maximal ideal $m \subset k[T_1, \dots, T_n]$ there is a unique $a \in k^n$ such that $ m = I({ a })$. This says that any maximal ideal is the ideal of some point.

Weak Nullstellensatz: implication 1 (Solutions)

every ideal, since it is contained in a maximal ideal, will have zeroes. Zeroes will always exist in all ideas upto the maximal ideal.

• It simply says that for all ideals $J$ in $\mathbb C[X_1, \dots, X_n]$, we have $I(V(J)) = sqrt J$
• Corollary: $I$ and $V$ are mutual inverses of inclusions between algebraic sets and radical ideals.

Weak Nullstellensatz: Implication 2 (Non-solutions)

If an ideal does not have zeroes, then it must be the full ring. Hence, 1 must be in this ideal. So if $I = (f_1, f_2, \dots, f_n)$ and the system has no solutions, then $I$ cannot be included in any maximal ideal, hence $I = \mathbb C[X_1, \dots, X_n]$. Thus, $1 \in I$, and there exist $c_i \in \mathbb C[X_1, \dots, X_n]$ such that $1 = sum_i f_i c_i$.

Strong Nullstellensatz: On the Tin

For every ideal $J$, we have that $I(V(J)) = |_0^\infty\sqrt J$. I am adopting the radical (heh) notation $|_0^\infty \sqrt x$ for the radical, because this matches my intuition of what the radical is doing: it's taking all roots, not just square roots. For example, $\sqrt{(8)} = (2)$ in $\mathbb Z$.

Strong Nullstellensatz: Implication 1 (solutions)

Let $J = (f_1, \dots, f_m)$. If $g$ is zero on $V(J)$ , then $g \in \sqrt J$. Unwrapping this, $\exist r \in \mathbb N, \exists c_i \in \mathbb C[X_1, \dots, X_n], \sum_i f_i c_i = g^r$.

Weak Nullstellensatz: Proof

• Let $m$ be a maximal ideal.
• Let $K$ be the quotient ring $K \equiv \mathbb C[X_1, \dots, X_n] / m$.
• See that $K$ is a field because it is a ring quotiented by a maximal ideal.
• Consider the map $\alpha: \mathbb C[X_1, \dots, X_n] \rightarrow K$, or $\alpha : \mathbb C [X_1, \dots, X_n] \rightarrow \mathbb C[X_1, \dots, X_n] / m$ by sending elements into the quotient.
• We will show that $\alpha$ is an evaluation map, and $K = \mathbb C$. So we will get a function that evaluates polynomials at a given point, which will have a single point as a solution.
• Core idea: See that $\alpha(\mathbb C) = \mathbb C \subset K$. Hence $K$ is a field that contains $\mathbb C$. But $\mathbb C$ is algebraically closed, hence $K = C$.
• First see that $\mathbb C \subset K$, or that $\alpha$ preserves $\mathbb C$ [ie, $\alpha(\mathbb C) = \mathbb C$]. note that no complex number can be in $m$. If we had a complex number $z$ in $m$, then we would need to have $1 = 1/z \cdot z$ in $m$ (since an ideal is closed under multiplication by the full ring), which means $1 \in m$, due to which we get $m$ is the full ring. This can't be the case because $m$ is a proper maximal ideal.
• Hence, we have $\mathbb C \subseteq K$ or $K = \mathbb C$.
• Thus the map we have is $\alpha: \mathbb C[X_1, X_2, \dots, X_n] \rightarrow \mathbb C$.
• Define $z_i = \alpha(X_i)$. Now we get that $\alpha(\sum_{ij} a_{ij} X_i^j) = \sum_{ij} a_{ij} z_i^j$. That is, we have an evaluation map that sends $X_i \mapsto z_i$.
• CLAIM: The kernel of an evaluation map $\alpha$ is of the form $(X_1 - z_1, \dots, X_n - z_n)$.
• PROOF OF CLAIM:TODO
• The kernel is also $m$. Hence, $m = (X_1 - z_1, \dots, X_n - z_n)$, and point that corresponds to the maximal ideal is $(z_1, z_2, \dots, z_n)$.

Strong Nullstellensatz: Proof

We use the Rabinowitsch trick.

• Suppose that wherever $f_1, \dots, f_m$ simultaneously vanish, then so does $g$. [that is, $g \in I(V(J))$ where $J = (f_1, \dots, f_m)$].
• Then the polynomials $f_1, \dots, f_m, 1 - Yg$ have no common zeros where $Y$ is a new variable into the ring.
• Core idea of why they can't have common zeros: Contradiction. assume that $1 - Yg$, and all the $f_i$ vanish at some point. Then we need $1 - Yg = 0$ which mean $Y = 1/g$, so $g$ cannot vanish, so $g \neq 0$. However, since all the $f_i$ vanish, $g$ also vanishes as $g \in (V(J))$. This is contradiction.
• Now by weak Nullstellensatz, the ideal $J = (f_1, \dots, f_m, (1-Y)g)$ cannot be contained in a maximal ideal (for then they would simultaneously vanish). Thus, $J = R$ and $1 \in J$.
• This means there are coefficients $c_i(Y, \vec x) \mathbb C[X_1, \dots , X_n, Y]$ such that

$$ 1 = c_0(Y, \vec x) (1 - Yg(\vec x)) \sum_{i=1}^m c_i(Y, \vec x) f_i(\vec x) $$

Since this holds when $\vec x, Y$ are arbitrary variables, it continues to hold on substituting $Y = 1/g$, the coefficient $c_0(1-Yg) = c_0(1 - g/g) = c_0(1 - 1) = 0$ disappears. This gives: $1 = \sum_{i=1}^m c_i (Y, \vec x) f_i(\vec x) $

since $Y = 1/g$, we can write $c_i(Y=1/g, \vec x) = n_i(\vec x)/g^r_i(\vec x)$. By clearing denominators, we get:

$$ 1 = \sum{i=1}^m n_i(\vec x) f_i(\vec x)/ g^R(\vec x) $$

This means that $ g^R(\vec x) = \sum_{i=1}^m n_i(\vec x) f_i(\vec x)$

Strong Nullstellensatz: algebraic proof

• We have $g \in I(V(J))$.
• We want to show that $g \in \sqrt{J}$ in $R$.
• This is the same as showing that $g \in \sqrt{0}$ in $R/J$. ($J \mapsto 0$ in the quotient ring).
• If $g$ is nilpotent in $R/J$, then the $(R/J)_g$ becomes the trivial ring ${ 0 }$. [Intuitively, if $g$ is nilpotent and a unit, then we will have $g^n = 0$, that is unit raised to some power is 0, from which we can derive $1 = 0$].
• Localising at $g$ is the same as computing $R[Y]/(1 - Yg, J)$.
• But we have that $V(1 - Yg, J) = \emptyset$. Weak Nullstellensatz implies that $(1 - Yg, J) = (1)$.
• This means that $R[Y]/(1 - Yg,J) = R[Y]/(1) = { 0 }$. Thus, $(R/J)_g$ has $g$ as nilpotent, or $g \in \sqrt J$ in $R$.

Relationship between strong and weak

Strong lets us establish what functions vanish on a variety. Weak let us establish what functions vanish at a point.

Strong Nullstellensatz in scheme theory

• Same statement: $I(V(J)) = \sqrt J$.
• $V(J)$ is the set of points on which $J$ vanihes. Evaluation is quotienting. So it's going to be set of prime ideals $p$ such that $J \xrightarrow{R/p} 0$. So $J \subset p$. This means that $V(J) = { p \text{prime ideal in } R, J \subseteq p }$.
• $I(V(J))$ is the set of functions that vanish over every point in $V(J)$. The functions that vanish at $p \in V(J)$ are the elements of $p$. So the functions that vanish over all points is $I(V(J)) = \cap V(J)$.
• Unwrapping, this means that $I(V(J))$ is the intersection of all ideals in $V(J)$, which is the intersection of all primes that contains $J$, which is the radical of $J$.

Holy shit, scheme theory really does convert Nullstellensatz-the-proof into Nullstellensatz-the-definition! I'd never realised this before, but this.. is crazy.

Not only do we get easier proofs, we also get more power! We can reason about generic points such as $(x)$ or $(y)$ which don't exist in variety-land. This is really really cool.

• Reference video

Screen recording for kakoune pull request

I wanted to show what keys I was pressing to demonstate the change I was proposing. So I used:

• SimpleScreenRecorder to record my screen.
• screenkey to show the keystrokes I press.

This was used the create the PR that improves the page up/page down to mimic vim behaviour

Intuition for why finitely presented abelian groups are isomorphic to product of cyclics

• If we have a finitely presented group, we can write any element as a product of the generators.. Say we have two genetors $g, h$ and some relations between them, we can have elements $gh$, $ghgh$, $gghh$, $ghg^{-1}$, and so on.
• If the group is abelian, we can rearrange the strings to write them as $g^a h^b$. For example, $ghgh = g^2h^2$, and $ghg^{-1} = g^0h^1$ and so on.
• Then, the only information about the element is carried by the powers of $g, h$.
• If $g$ has order $n$ and $h$ has order $m$, then the powers live in $Z/nZ, Z/mZ$.
• Thus, the group above is isomorphic to $Z/nZ \times Z/mZ$ by rearranging and collecting powers.
• The same argument works for any finitely generated abelian group.

Alternative orderings for segtrees (WIP)

Group structure of nim games (WIP)

Mex

Euler characteristic of sphere

Pick two antipodal points and connect them into a great circle. We have two points. To connect them, we need two edges. The great circle divdies the spere into two faces. This gives $2-2+2=2$.

John Conway: The symmetries of things

Original way to classify wallpaper groups: think of geometric transforms that fix the pattern. Thurston's orbifold solution: think of quotients of $\mathbb R^2$ by groups --- this gives you an orbifold (orbit manifold).

Take a chair, surround it around by a sphere. The symmetries of a physical object fixes the center of gravity. So we pick the center of the sphere to be the center of gravity. The "celestial sphere" (the sphere around the chair) is a nice manifold (We only have the surface of the sphere). The vertical line that divides the chair also divides the sphere into two parts.

• The points of the orbifold are orbits of the group.
• So now the orbifold gives us a hemisphere in this case.
• The topology of the orbifold determines the group.
• This is astonishing, because the group is a metrical object: elements of the group preserve the inner product of the space.
• And yet, geometrical groups are determined by the topology of their orbifolds!
• Thurston's metrization conjecture: certain topological problems reduce to geometrical ones.

Conway came up with his notation for wallpaper groups/orbifolds. There are only four types of features.

• The hemisphere orbifold is *. (group of order 2). * denotes the effect on the orbifold. * really means: what is left out of a sphere when I cut out a hemispherical hole. * is the name for a disk, because a hemisphere is a disk topologically. It has metrical information as well, but we're not going to speak about it, because all we need is the topological information.
• One-fourth of a sphere (symmetry group of rectangular table) is denoted by * 2 2. The * for the hemisphere, and 2, 2 for the angles of pi/2.
• If the table is a sphere, then we have diagonal symmetry as well. In this case, the orbifold has angle pi/4. So the table is * 4 4.
• If we take a cube, then we have an even more complicated orbifold. The "fundamental region" of the cube has 2, 3, and 4 mirrors going through them. So in the orbifold, we get triangles of angles pi/2, pi/3, pi/4. This would be * 4 3 2.
• Draw a swastika. This has no reflection symmetry. This has a gyration: a point about which the figure can be rotated, but the point is NOT on a line of reflection. We can tear the paper and make it into a cone. This gives us a cone point. The angle around the cone point is 2pi/4. This is the orbifold of the original square with a swastika on it.

An orbifol can be made to carry some amount of metrical information. The cone point only has 90 degrees, so it is in some sense, "a quarter of a point".

• Draw a cube with swastikas marked on each face. This has no reflection symmetry. Once again, we have a gyration, and again, only the gyration/singularities matter. This group is again 4, 3, 2 , but in blue. In this notation, red is reflection, blue is "true motion" (?).

Let us try to work out the euler characteristic of the rectangular table orbifold by using $V - E + F$. The orbifold as one face. The wrong thing to say is that the orbifold has two edges and two vertices. It is untrue because the edge of the orbifold is only half an edge --- let's say that lines have thickness. In this case, we will have $V = 2/4$, $E = 2/2$, and $F = 1$. The euler characteristic works out to be a half. This is appropriate, because the orbifold is a type of divided manifold.

• If we work this out for a cube, we get $2/48$. This is because the sphere gets divided into 48 pieces, and the sphere has an euler characteristic of 2!
• Alternatively, we can think that we started out with 2 dollars, and we are then buying the various features of our orbifold. * costs 1$, a blue number after a star, for example: 2 costs 1/2 a dollar. 3 costs 2/3 of a dollar, 4 costs 3/4 of a dollar. In general, n costs 1 - 1/n. The red numbers are children, so they cost half an much: n consts 1/2(1 - 1/n) = (n-1)/2n.

Now, see that we started with positive euler characteristic (2), and we divide it by some n (the order of the group). So we end up with a positive euler characteric. By a sort of limiting argument, the euler characteristic of the wallpaper groups, which are infinite, is zero. However, see that we must get to the zero by starting with two dollars and buying things off the menu! If we try and figure out what all the possible ways are to start with 2 dollars and buy things till we are left with exactly 0 dollars, we get that there are 17 possible ways of buying things on the menu! Thus, this the reason for there being 17 wallpaper groups.

• To buy more than two dollars, you are buying symmetries from the hyperbolic plane!

Because we can completely enumerate 2-manifolds, we can completely enumerate 2-orbifolds, which are essentially the same thing as symmetry groups. The real power is in the 3D case. We don't have a full classification of 3-manifolds. But we maybe able to go the other way. This is the metrization theorem.

• Video lecture

Semidirect product mnemonic

I just learnt that when we write the semidirect product $N \ltimes K$, the $\ltimes$ is to look like a combination of $N \triangleleft G$ ($N$ is normal in $G$) and the $\times$ operator; This tells us that it is the $N$ part that is normal. in $N \ltimes K$.

• A good example to remember is $\mathbb R^3 \ltimes SO(3)$, where we define a group element $(t, r)$ by the action: $(t, r) v = rv + t$ [$t$ for translation and $r$ for rotation].

• Let's compose these. We find that:

$$ \begin{aligned} &(t2, r2)((t1, r1)(v)) \ &= (t2, r2)(r1v + t1) \ &= r2(r1v + t1) + t2\ &= (r2 r1) v + (r2 t1 + t2) \ &= (r2 t1 + t2, r2 21) v \end{aligned} $$

• Here, we have the rotation $r_2$ act non-trivially on the translation $t_1$.
• We need the translation to be normal, since we are messing with the translation by a rotation.
• We want the translations to be closed under this messing about by the rotation action; The action of a rotation on a translation should give us another translation. Thus, the translations $(t_1, id)$ ought to be normal in the full group $(t_2, r_2)$.

Another mnemonic for the semidirect product:

my thesis adviser told me that the acting group (the non-normal subgroup) opens its mouth and tries to swallow / "act on" the group it acts upon (the normal subgroup). The group that is acted on must be normal, because we act "by conjugation". Alternatively, being normal is "tasty", and thus needs to be eaten.

Non orthogonal projections

Consider the matrix

$$ P = \begin{bmatrix} 1 & 1 \ 0 & 0 \end{bmatrix} $$

• $P^2 = P$, so it's a projection. It projects the vector [x;y] to the vector [x+y;0]. Clearly, applying it twice will result in 0. [x; y],
  1. [x+y; 0], 2. [x+y; 0].
• It projects the value (x+y)onto the x axis,and kills the y axis.
• It's not a projection onto the coordinate axis.

Why did maxwell choose his EM wave to be light?

• We Knew gravity as fields
• dalton/thompson atomic model that had particles: protons, neutrons, electron
• Knew electricity and magnetism as fields
• Maxwell wrote down laws, said that the wave solution to his laws was light. (why?)
• Michaelson morly proved speed of light was constant, matched maxwell prediction
• Einstein found photo electric effect. Posited “light particle” (photon). [why light?]
• De Broglie
• [who connected photon to EM wave through gauge?]
• Weyl created U(1) symmetry for Maxwell’s equations / photon
• Yang-mills wrote down how photon occurs as particle associated to EM field
• what is the field that electron corresponds to? Electron field? Why no wiki page? Dirac spinor field! Dirac spinor
• How do we get fermi/bose statistics out of the field equation? In QM, when we perform second quantization, ie, solve for single particle and claim that multi particle is the tensoring of single particle, we “choose the statistics” arbitrarily.

Fast string concatenation in python3

Apparently, the correct way to do this, in a way that's not O(n^2) is to use the io.StringIO module. The API is:

• x = io.StringIO(): create a string buffer
• x.write(stuff_to_append): append into string buffer with correct realloc() doubling semantics for O(1) amortized per character
• out = x.getvalue(): pull data out of StringIO.
• x.close(): tell the StringIO that we are done and it can free its buffer.

It took quite a bit of trawling the API docs to find this while I was helping a friend speed up some data munging.

Split infinitive

to safely remove %v

The infinite "to remove" has been split by "safely".

to remove %v safely.

Yoneda from string concatenation (WIP)

I'm trying to build intuition for Yoneda (again) this time from the perspective of strings and concatenation. The idea is that the identity function behaves like the empty string, and "free arrow composition" behaves like string concatenation. So can we understand yoneda from this model?

• First, let's think of Hom(X, X). What are the elements here? Well, for one, we need the identity arrow idX in Hom(X, X). Maybe we have other elements called a, b, c in Hom(X, X). So our picture of Hom(X, X) looks like this:

• what does it mean to have an element a in Hom(X, X)? It means that there's an arrow from X to X in the category. But this also means that we have a map from Hom(X, X) to Hom(X, X), given by composing with a! That is, we have a map - . a :: Hom(X, X) -> Hom(X, X).

• If we have such a map of "composition with a", then we need to know where this map -.a maps all the elements of Hom(X, X). Thinking about this, we see that we need to add new elements to Hom(X, X), which are the composition of the current elements (idX, a, b, c) with a. This gives us the elements idX.a = a, a.a = aa, b.a = ba, c.a = ca.

• Similarly, we need to know where these new elements aa, ba, ca map to, but let's hold off on that for now, for that simply demands an extrapolation of imagination. Let's imagine having another object Y and an arrow g: X -> Y. This will give us a new hom-set Hom(X, Y) = Hom(X, X) . g

• In Hom(X, Y) we will have as elements all the arrows from X to Y. Let's say there's some arrow h: X -> Y. Then, we will find this arrow h in Hom(X, Y) as the image of idX under -.h . So really, for any arrow, we can find what element it maps to as long as know (a) idX and (b) -.h.

Now that we understand the "internal" structure, let's imagine we're representing this collection of objects and arrows by some other collection of objects and arrows. So we have a functor F that takes these sets to other sets, and takes these objects to other objects.

Right Kan extensions as extending the domain of a functor (WIP)

First over functions (fake category fluff)

Given a function $g: C \rightarrow E$ and an embedding $j: C \rightarrow D$, then the Right Kan extension of $g$ along $j$, denoted $g/j$ is a new function $g/j: D \rightarrow E$. So we are extending the domain of $g$, along the extender $j$. Informally, we write the new function as $g/j$ because:

C---
|   \-g---*
j         |
|         |
v         v
D--g/j--->E

foo(j(c)) = g(c)
foo = (g/j)(c) 
g/j(j(c)) = g(c)

Next over preorders (real category stuff)

The kan extension provides us a bijection, for any function f: D -> E

C---
|   \-g---*
j         |
|         |
v         v
D--g/j--->E
D------f->E

hom(f.j, g) ~= hom(f, g/j)

That is, if we have some way to make congruent f.j with g, then we can "split" the congruence to have f.j congruent with (g/j).j. Cancelling j, we can have f congruent with g/j.

Consider a preorder with a ordering ≤. Equip with a monoidal structure <>, which is a monotone map with a neutral element. (For example, integers with multiplication and ≤).

The bijection of hom-sets is equivalent to saying

m*k <= n iff m <= n/k

(how? I have no idea; I gotta work this out!)

Question: What happens in the context of vector spaces?

Since linear algebra is probably the nicest thing we have in math, I really want to understand what happens in the linear algebra case. I don't really understand how to make the correct version of a kan extension inside $Vect$, though. A kan extension seems to fundamentally be a 2 categorical construct, than a 1 categorical construct.

• Art and dan explain an old trick

Non standard inner products and unitarity of representations

I stumbled across this questions about non-standard inner products. Can I use this to visualize the weyl averaging trick in represention theory?

take at most 4 letters from 15 letters.

Trivial: use $\binom{15}{0} + \binom{15}{1} + \binom{15}{3} + \binom{15}{4}$. Combinatorially, we know that $\binom{n}{r} + \binom{n}{r-1} = \binom{n+1}{r}$. We can apply the same here, to get $\binom{15}{0} + \binom{15}{1} = \binom{16}{1}$. But what does this mean, combinatorially? We are adding a dummy letter, say $d_1$, which if chosen is ignored. This lets us model taking at most 4 letters by adding 4 dummy letters $d_1, d_2, d_3, d_4$ and then ignoring these if we pick them up; we pick 4 letters from 15 + 4 dummy = 19 letters.

I find it nice how I used to never look for the combinatorial meaning behind massaging the algebra, but I do now.

Flat functions

Define

$$ f(x) \equiv \begin{cases} 0 & x <= 0 \ e^{-1/x} & x > 0 \end{cases} $$

This is smooth, but is badly non-analytic. Any taylor expansion around $x=0$ is going to be identically zero. So we're going to prove that it possesses all derivatives. This implies that the derivative at zero is equal to zero, because the left derivative is always equal to zero.

• $f(x) \equiv e^{-1/x}$. Differentiate to get $f'(x) = e^{-1/x}/x^2$. Change $y \equiv 1/x$ to get $y^2 e^{-y}$. As $y \mapsto \infty$, $e^{-y}$ decays more rapidly than $y^2$ increases, thus the limit is zero. Hence, $f'(x) = 0$.
• For higher derivatives, let $f^{(n)}(x) \equiv p_n(1/x) e^{-1/x}$ for some polynomial $p_n$. See that $f^{(n+1)}(x) = d/dx [p_n(1/x) e^{-1/x})]$. To compute this, set $y \equiv 1/x$ and compute $d/dy [p_n(y) e^{-y}] dy/dx$ which is:

$$ \begin{aligned} & = d/dy [p_n(y) e^{-y}] dy/dx \ & = p_n'(y) e^{-y} + p_n(y) (- e^{-y}) \cdot 1/x^2 \ & = e^{-1/x} (p_n'(1/x) - p_n(1/x)) 1/x^2 \ & = e^{-1/x} (q_n'(1/x) - q_n(1/x)) \ & \text{let $r_{n+1}(x) (\equiv q_n'(t) - q_n(t))t^2$} \ & = r_{n+1}(1/x) e^{-1/x} \end{aligned} $$

• So we can write higher derivatives too as $poly(1/x)$ times $exp(-1/x)$ which also decays rapidly to $0$.

• Flat functions on wikipedia

Hopf Algebras and combinatorics (WIP)

Started from algebraic topology in the 40s. In late 70s, Rota figured out that many combinatorial objects have the structure of a Hopf algebra.

A hopf algebra is a vector space $H$ over a field $K$. together with $K$ linear maps $m: A \rightarrow A \otimes A$ (multiplication), $U: A \rightarrow K$ (unit), $\Delta: H \rightarrow H \otimes H$ (comultiplication) $S: A \rightarrow A$ (co-inverse/antipode). Best explained by examples!

• Hopf algebra and combinatorics

• Hopf algebras and rooted trees

• Hopf algebra 1

The idea is that groups act by symmetries. Hopf algebras also act, we can think of as providing quantum symmetries.

Eg 1: Group algebra: $A = kG$

$G$ is a group, $kG$ is a group algebra. $\delta(g) \equiv g \otimes g$, $\epsilon(g) = 1$, $s(g) = g^{-1}$.

Butcher group

I really want to read the math about the butcher group, which was introduced to study numerical solutions of ODEs using RK, and then had far-reaching theoretical applications. Connes remarked:

We regard Butcher’s work on the classification of numerical integration methods as an impressive example that concrete problem-oriented work can lead to far-reaching conceptual results.

Neovim frontends

• veonim: Rendered an utterly glitched UI.
• uivonum: NPM based, so wasn't my thing.
• neovide: rust based, feels very fluid, has cool cursor animations that make it "fun" to type with!
• goneovim

A semidirect product worked on in great detail

We work out the semidirect product structure of the collection of real 2x2 matrices

$$ \begin{bmatrix} 1 & a \ 0 & b \end{bmatrix} $$

We first see that the multiplication rule is:

$$ \begin{bmatrix} 1 & a \ 0 & b \end{bmatrix} \begin{bmatrix} 1 & p \ 0 & q \end{bmatrix}

\begin{bmatrix} 1 & p + bq \ 0 & bq \end{bmatrix} $$

so these are closed under matrix multiplication. The identity matrix is one among these matrices and thus we have the identity. The inverse of such a matrix can also be seen to be of such a kind.

Diagonal transforms

We have two subgroups of matrices in this set of 2x2 matrices. The first of these I shall call diagonal and denote with $D$:

$$ \begin{bmatrix} 1 & 0 \ 0 & b \end{bmatrix} \begin{bmatrix} 1 & 0 \ 0 & q \end{bmatrix}

\begin{bmatrix} 1 & 0 \ 0 & bq \end{bmatrix} $$

Hopefully clearly, this is isomorphic to $\mathbb R^*$ since the only degree of freedom is the bottom right entry, which gets multiplied during matrix multiplication. These transform a vector $(x, y)$ into the vector $(x, \delta y)$. Informally, the $D$ matrices are responsible for scaling the $y$-axis.

Shear transforms

Next, we have the other subgroup of matrices, which I shall call shear and denote by $S$:

$$ \begin{bmatrix} 1 & a \ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & p \ 0 & 1 \end{bmatrix}

\begin{bmatrix} 1 & (a+p) \ 0 & 1 \end{bmatrix} $$

These are isomorphic to $\mathbb R^+$, since the only degree of freedom is their top-right entry, which gets added on matrix multiplication. These matrices transform a vector $(x, y)$ into $(x + \delta y, y)$.

Generating all transforms with diagonal and shear transforms

we can write any transform of the form

$$ T \equiv \begin{bmatrix} 1 & a \ 0 & b \end{bmatrix} $$

Semidirect product: Conjugations

We need to check whether the subgroup $D$ or the subgroup $S$ is normal. For this, take two arbitrary elements:

$$ [d] \equiv \begin{bmatrix} 1 & 0 \ 0 & d \end{bmatrix}; ~~~ [s] \equiv \begin{bmatrix} 1 & s \ 0 & 1 \end{bmatrix} $$

Conjugating $D$ by $S$:

Let's to conjugate a diagonal with a shear:

$$ \begin{aligned} &[s^{-1}][d][s](x, y) \ &= [s^{-1}][d] (x+sy, y) \ &= [s^{-1}](x+sy, dy) \ &= (x+sy-sdy, dy) \ \end{aligned} $$

This doesn't leave us with another diagonal transform.

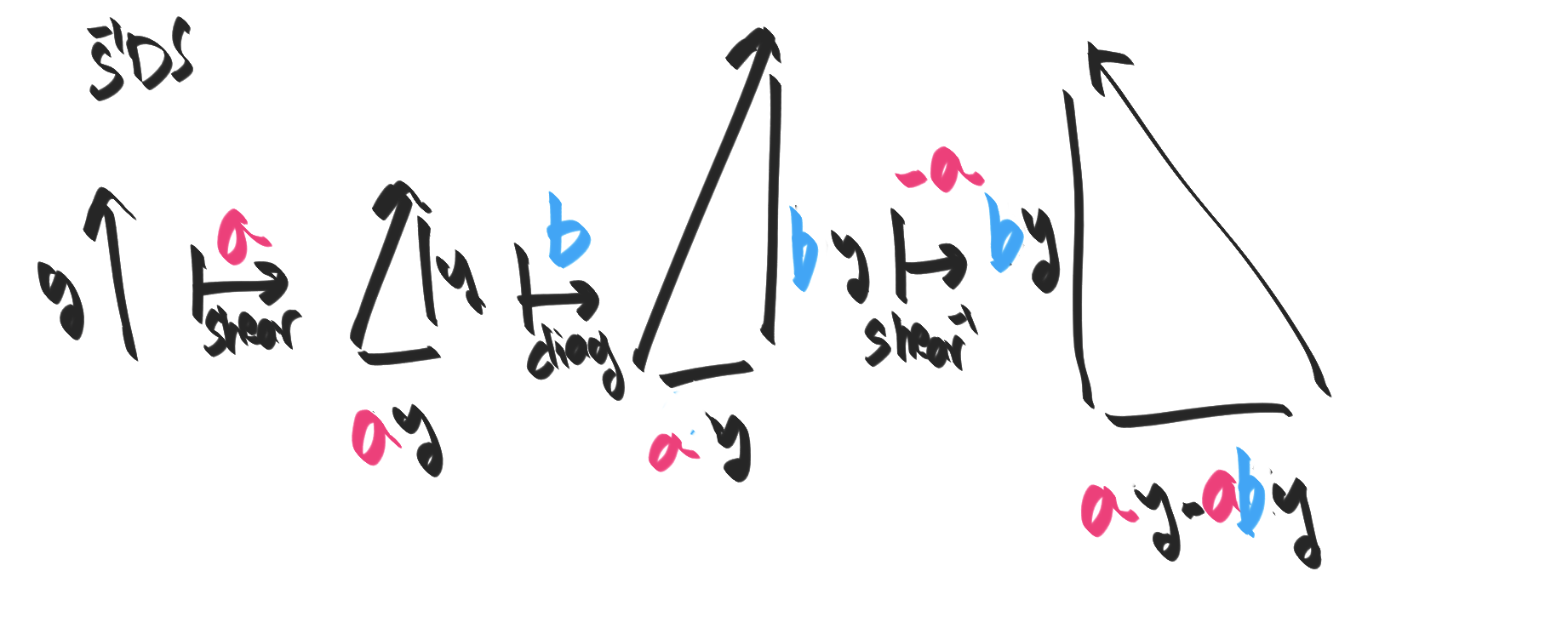
Conjugating $S$ with $D$

Now let's compute the action of $dsd^{-1}$, and $sds^{-1}$ on some general $(x, y)$:

$$ \begin{aligned} &[d^{-1}][s][d](x, y) \ &= [d^{-1}][s] (x, dy) \ &= [d^{-1}](x + dy, dy) \ &= [d^{-1}](x + dy, dy \times 1/d \ &= (x + dy, y) \end{aligned} $$

See that the final result we end up with is a shear transform which shears by $y/d$. So, we can write the equation $DSD^{-1} = S$: conjugating a shear by scaling leaves us with a shear.

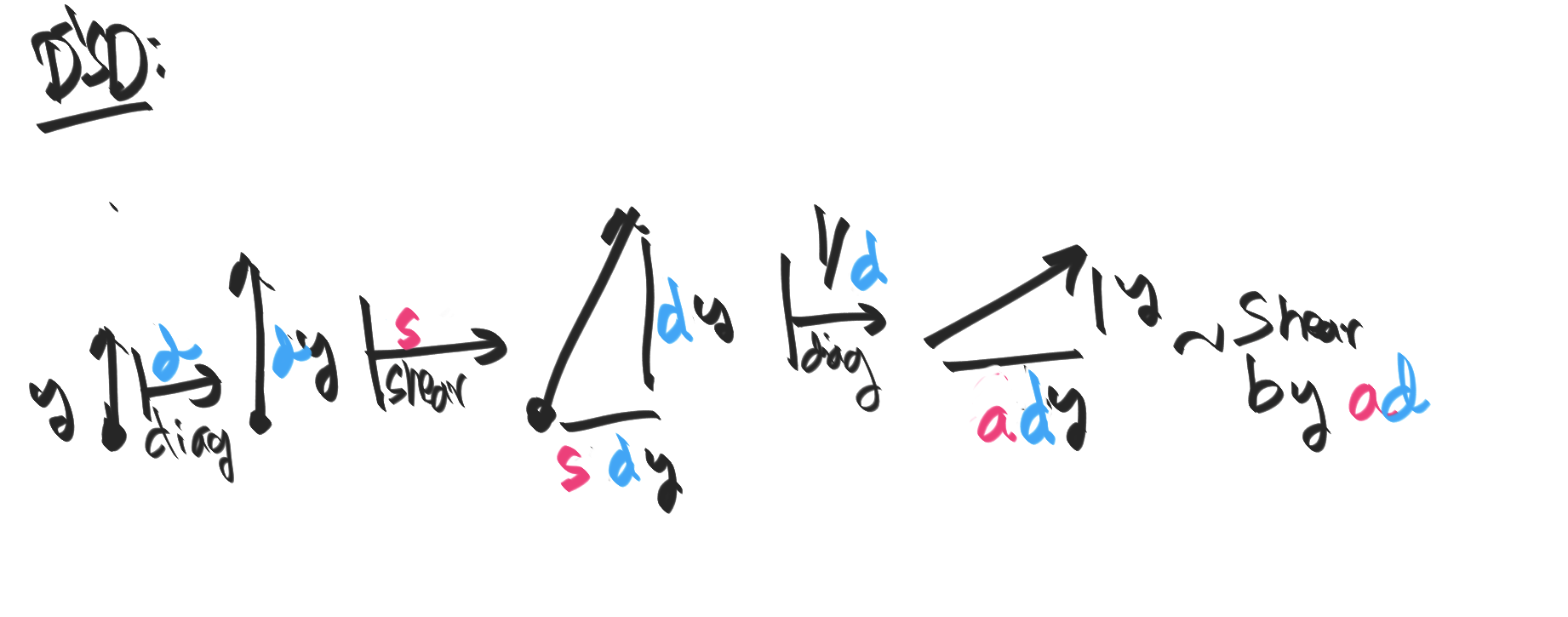
The connnection to partial fractions

Recall that any matrix of the form [a b; c d] can be viewed as taking the fraction x/y to (ax+by)/(cx+dy). In our case, we have:

• Diagonal: [1 0; 0 b] which take x/y to x/by.
• Shear: [1 a 0 1] which take x/y to (x + ay)/y.

It's clear that diagonals and shears compose. What is unclear is how they interact. A little thought shows us:

x/y -diagonal->
x/dy -shear->
(x+sdy)/dy
(x+sy')/y'

x/y -shear->
(x+sy)/y -diagonal->
(x+sy)/dy
= (x+(s/d)y')/y'

So, when we compse shears with diagonals, we are left with "twisted shears". The "main objects" are the shears (which are normal), and the "twists" are provided by the diagonal.

The intuition for why the twisted obect (shears) should be normal is that the twisting (by conjugation) should continue to give us twisted objects (shears). The "only way" this can resonably happen is if the twisted subgroup is normal: ie, invariant under all twistings/conjugations.

How the semidirect product forms

From the above computations, we can see that it is the shear transform $S$ that are normal in the collection of matrices we started out with, since $D^{-1}SD = S$. Intuitively, this tells us that it is the diagonal part of the transform composes normally, and the shear part of the transform is "twisted" by the diagonal/scaling part. This is why composing a shear with a diagonal (in either order --- shear followed by diagonal or vice versa) leaves us with a twisted shear. This should give a visceral sense of "direct product with a twist".

Where to go from here

In some sense, one can view all semidirect products as notationally the same as this example so this example provides good intuition for the general case.

Direct and Inverse limits

Direct limit: definition

A direct limit consists of injections $A_1 \rightarrow A_2 \rightarrow \dots$. It leads to a limit object $L$, which as a set is equal to the union of all the $A_i$. It is equipped with an equivalence relation. We can push data "towards" the limit object, hence it's a "direct" limit.

So each element in $A_i$ has an equivalence class representative in $L$.

Direct limit: prototypical example

$S_n$

We can inject the symmetric groups $S_1 \rightarrow S_2 \rightarrow \dots$. However, we cannot project back some permutation of $S_2$ (say) to $S_1$: if I have $(2, 1)$ (swap 2 and 1), then I can't project this back into $S_1$.

This is prototypical; in general, we will only have injections into the limit, not projections out of the limit.

Prufer group

Here, the idea is to build a group consisting of all the $p^n$th roots of unity. We can directly """define""" the group as:

$$ P(q)^\infty \equiv { \texttt{exp}(2\pi k /q^n) : \forall n, k \in \mathbb N, ~ 0 \leq k \leq q^n } $$

That is, we take $q^1$th roots of unity, $q^2$th roots of unity, and so on for all $n \in \mathbb N$.

To build this as a direct limit, we embed the group $Z/q^n Z$ in $Z/q^{n+1}Z$ by sending: the $q^n$ th roots of unity to $q^{n+1}$th roots of unity raised to the power $q$. An example works well here.

• To embed $Z/9Z$ in $Z/27Z$, we send:
• $2 \pi 1 /9$ to $2 \pi 1/9 \times (3/3) = 2 \pi 3 / 27$.
• $2 \pi 2 /9$ to $2 \pi 6/27$
• $2 \pi 3 /9$ to $2 \pi 9 / 27$
• $2 \pi k / 9$ to $2 \pi (3k)/27$
• This gives us a full embedding.

The direct limit of this gives us the prufer group. We can see that the prufer group is "different" from its components, since for one it has cardinality $\mathbb N$. For another, all subgroups of the prufer group are themselves infinite. The idea is to see that:

• Every subgroup of the prufer group is finite.
• By Lagrange, |prufer|/|subgroup| = |quotient|. But this gives us something like infinite/finite = infinite.

To see that every subgroup $H$ of the prufer group is finite, pick an element $o$ outside of the subgroup $H$. This element $o$ will belong to some $Z/q^kZ$ for some $k \in \mathbb Z$ (since the direct limit has an elements the union of all the original elements modulo some equivalence). If the subgroup $H$ does not have $o$ (and thus does not contain $Z/q^kZ$), then we claim that it cannot contain any of the larger $Z/q^{k+\delta}Z$. If it did contain the larger $Z/q^{k + \delta}$, then it would also contain $Z/q^k$ since we inject $Z/q^k$ into $Z/q^{k+\delta}$ when building the prufer group. Thus, at MAXIMUM, the subgroup $H$ can be $Z/q^{k-1}Z$, or smaller, which is finite in size. Pictorially:

...         < NOT in H
Z/q^{k+1}Z  < NOT IN H
Z/q^kZ      < NOT IN H
---------
...         < MAYBE IN H, FINITE
Z/q^2Z      < MAYBE IN H, FINITE
Z/qZ        < MAYBE IN H, FINITE

The finite union of finite pieces is finite. This $H$ is finite.

Stalks

Given a topological space $(X, T)$ and functions to the reals on open sets $F \equiv { U \rightarrow \R }$, we define the restricted function spaces $F|_U \equiv { F_U : U \rightarrow \mathbb R : f \in F }$.

Given two open sets $U \subseteq W$, we can restrict functions on $W$ (a larger set) to functions on $U$ (a smaller set). So we get maps $F|_W \rightarrow F|_U$.

So given a function on a larger set $W$, we can inject into a smaller set $U$. But given a function on a smaller set, it's impossible to uniquely extend the function back into a larger set. These maps really are "one way".

The reason it's a union of all functions is because we want to "identify" equivalent functions. We don't want to "take the product" of all germs of functions; We want to "take the union under equivalence".

Finite strings / A*

Given an alphabet set $A$, we can construct a finite limit of strings of length $0$, strings of length $1$, and so on for strings of any given length $n \in \mathbb N$. Here, the "problem" is that we can also find projection maps that allow us to "chop off" a given string, which makes this example not-so-great. However, this example is useful as it lets us contrast the finite and infinite string case. Here, we see that in the final limit $A*$, we will have all strings of finite length. (In the infinite strings case, which is an inverse limit, we will have all strings of infinite length)

Vector Spaces over $\mathbb R$

consider a sequence of vector spaces of dimension $n$: $V_1 \rightarrow V_2 \dots V_n$. Here, we can also find projection maps that allows us to go down from $V_n$ to $V_{n-1}$, and thus this has much the same flavour as that of finite strings. In the limiting object $V_\infty$, we get vectors that have a finite number of nonzero components. This is because any vector in $V_{\infty}$ must have come from some $V_N$ for some $N$. Here, it can have at most $N$ nonzero components. Further, on emedding, it's going to set all the other components to zero.

Categorically

Categorically speaking, this is like some sort of union / sum (coproduct). This, cateogrically speaking, a direct limit is a colimit.

Inverse limit: definition

An inverse limit consists of projections $A_1 \leftarrow A_2 \leftarrow \dots$. It leads to a limit object $L$, which as a set is equal to a subset of the product of all the $A_i$, where we only allow elements that "agree downwards" .Formally, we write this as:

$$ L \equiv { a[:] \in \prod_i A_i : \texttt{proj}(\alpha \leftarrow \omega)(a[\omega]) = a[\alpha] ~ \forall \alpha \leq \omega } $$

So from each element in $L$, we get the projection maps that give us the component $a[\alpha]$.

These 'feel like' cauchy sequences, where we are refining information at each step to get to the final object.

Inverse limit: prototypical example

infinite strings

We can consider the set of infinite strings. Given an infinite string, we can always find a finite prefix as a projection. However, it is impossible to canonically inject a finite prefix of a string into an infinite string! Given the finite string xxx, how do we make it into an infinite string? do we choose xxxa*, xxxb*, xxxc*, and so on? There's no canonical choice! Hence, we only have projections, but no injections.

P-adics

Consider the 7-adics written as infinite strings of digits in ${0, 1, \dots, 6}$. Formally, we start by:

1. Having solutions to some equation in $\mathbb{Z}/7\mathbb{Z}$
2. Finding a solution in $\mathbb{Z}/49\mathbb{Z}$ that restricts to the same solution in $\mathbb{Z}/7\mathbb{Z}$
3. Keep going.

The point is that we define the $7$-adics by projecting back solutions from $\mathbb{Z}/49\mathbb{Z}$. It's impossible to correctly embed $\mathbb{Z}/7\mathbb{Z}$ into $\mathbb{Z}/49\mathbb{Z}$: The naive map that sends the "digit i" to the "digit i" fails, because:

• in $\mathbb{Z}/7\mathbb{Z}$ we have that $2 \times 4 \equiv 1$.
• in $\mathbb{Z}/49\mathbb{Z}$ $2 \times 4 \equiv 8$.

So $\phi(2) \times \phi(7) \neq \phi(2 \times 7) = \phi(4)$. Hece, we don't have injections, we only have projections.

Partitions

Let $S$ be some infinite set. Let ${ \Pi_n }$ be a sequence of partitions such that $\Pi_{n+1}$ is finer than $\Pi_n$. That is, every element of $\Pi_n$ is the union of some elements of $\Pi_{n+1}$. Now, given a finer partition, we can clearly "coarsen" it as desired, by mapping a cell in the "finer space" to the cell containing it in the "coarser space". The reverse has no canonical way of being performed; Once again, we only have projections, we have no injections.

The inverse limit is:

$$ { (P_0, P_1, P_2, \dots) \in \prod_{i=0}^n \Pi_n : P_a = \texttt{proj}_{a \leftarrow z}(P_z) \forall a \leq z }. $$

But we only care about "adjacent consistency", since that generates the other consistency conditions; So we are left with:

$$ { (P_0, P_1, P_2, \dots) \in \prod_{i=0}^n \Pi_n : P_a = \texttt{proj}_{a \leftarrow b}(P_b) \forall a +1 = b }. $$

But unravelling the definition of $\texttt{proj}$, we get:

$$ { (P_0, P_1, P_2, \dots) \in \prod_{i=0}^n \Pi_n : P_a \supseteq P_b) \forall a +1 = b }. $$

So the inverse limit is the "path" in the "tree of partitions".

Vector Spaces

I can project back from the vector space $V_n$ to the vector space $V_{n-1}$. This is consistent, and I can keep doing this for all $n$. The thing that's interesting (and I believe this is true), is that the final object we get, $V^\omega$, can contain vectors that have an infinite number of non-zero components! This is because we can build the vectors:

$$ \begin{aligned} &(1) \in V_1 \ &(1, 1) \in V_2 \ &(1, 1, 1) \in V_3 \ &(1, 1, 1, 1) \in V_4 \ &\dots \end{aligned} $$

Is there something here, about how when we build $V_\infty$, we build it as a direct limit. Then when we dualize it, all the arrows "flip", giving us $V^\omega$? This is why the dual space can be larger than the original space for infinite dimensional vector spaces?

Categorically

Categorically speaking, this is like some sort of product along with equating elements. This, cateogrically speaking, a inverse limit is a limit (recall that categorical limits exist iff products and equalizers exist).

Poetically, in terms of book-writing.

• The direct limit is like writing a book one chapter after another. Once we finish a chapter, we can't go back, the full book will contain the chapter, and what we write next must jive with the first chapter. But we only control the first chapter (existential).

• The inverse limit is like writing a book from a very rough outline to a more detailed outline. The first outline will be very vague, but it controls the entire narrative (universal). But this can be refined by the later drafts we perform, and can thus be "refined" / "cauchy sequence'd" into something finer.

Differences

• The direct limit consists of taking unions, and we can assert that any element in $D_i$ belongs in $\cup_i D_i$. So this lets us assert that $d_i \in D_i$ means that $d_i \in L$, or $\exists d_i \in L$, which gives us some sort of existential quantification.
• The inverses limit consists of taking $\prod_i D_i$. So given some element $d_i \in D_i$, we can say that elements in $L$ will be of the form ${d_1} \times D_2 \times D_3 \dots$. This lets us say $\forall d_1 \in D_1, {d_1} \times D_2 \dots \in L$. This is some sort of universal quantification.

LEAN 4 overfrom from LEAN together 2021

• add unsafe keyword.
• allow people to provide unsafe version of any opaque function if the type is inhabited. Type inhabited => proofs are fine. (Do we need to assume UIP for this to work?)
• mimalloc, custom allocator.
• counting immutable beans for optimising refcounting. (related work: Perceus: Grabage free refcounting with reuse.)
• hash tables and arrays are back (thanks to linearity?)
• Tabled typeclass resolution for allowing diamonds in typeclass resolution (typeclasses no longer need to form a semilattice for resolution).
• Discrminiation trees.
• LEAN4 elaborator for adding custom syntax related to monads, tactics.
• Beyond notation: hygenic macro expansion for theorem proving languages.
• Kernel can have external type checker.

during wartime, you do not study the mating ritual of butterflies

• Collaboration: Optimising tensor computations.
• Collaboration: Rust integration.
• Collaboration: DSLs for LEAN.
• Collaboration: SAT/SMT integration

Metaprogramming in LEAN4

• macro expansion, elaboration. First expand all macros, elaborate, repeat.

Verified decompilation

• We want assured decompilation.

• Check equivalence of BBs using solvers; compcert approach is too complex.

• Lean together 2021

BLM master thesis

• link here

Hololive subculture

• hololive artists

RSK correspondence for permutations

Tableaux

Tableaux of size $n$ first needs a partition of size $n$ in decreasing order. Write it as $\lambda$, such that $\lambda[i] \geq 0$ and $\sum_i \lambda[i] = n$ and $\lambda[i]$ is weakly decreasing: $\lambda[1] \geq lambda[2] \geq lambda[n]$. For example, a partition of $9$ is $4, 2, 2, 1$. This is drawn as:

* * * *
* *
* *
*

Next, we fill the tableau with numbers from $[n] \equiv {1,\dots,n}$ such that the rows are weakly increasing and columns are strictly increasing (gravity acts downwards, and we always want to get bigger). These are called Standard tableay For example, a valid Standard tableau corresponding to the partition above is:

1 3 4 6
2 5 
7 9
8

(Sidenote: here both rows and columns are strictly increasing because we have unique numbers. If we did not, then by convention, the rows will be weakly increasing and columns strictly increasing. I always repeat the chant "rows weakly, columns strictly" to burn it into my brain).

Insertion

Say we start with some tableau $T$. Can we add an element $x$ into it such that $T' = ins(T, x)$ is a valid tableau? Yes, and this process is called insertion.

Deletion

This is the reverse of insertion. Say we start with a tableau $T$. Can we delete a location $(i, j)$, such that we get a smaller tableau $T'$, and an element $x$ such that $ins(T', x) = T$? Yes we can, and this process is called deletion.

Misoncentions about deletion

Deletion does not mean that we lose the value at $(i, j)$. Rather, we change the shape of the tableau to lose the cell $(i, j)$. consider the tableau:

1
2
3

If we ask to delete the cell $(r=1,c=3)$ (that is, the cell containing $3$), we will be left with the tableau:

2
3

and the element $1$. So, when we insert $1$ into $[2; 3]$ we get $[1; 2; 3]$.

We did not get

1
2

and the element $3$. This is because if we insert $3$ into $[1;2]$, then we get the tableau $[1,3;2]$:

1 3
2

Bijection between permutations and pairs of standard tableau

Given a permutation $p: [n] \rightarrow [n]$, we define two tableau corresponding to it: the insertion tableau $P$ and the recording tableau $Q$. Informally, the insertion tableau is obtained by inserting $p[1], p[2], \dots, p[n]$ in sequence into an empty tableau. The recording tableau at step $i$ records where the number $i$ was stored in the tableau. So the recording tableau at step $i$, $Q_i$ has the same shape as the insertion tableau at step $i$, $P_i$, and contains the value $i$ at the cell where $i$ was stored in $P$. That is, $P_i[Q_i[i]] = i$.

Properties of the insertion and recording tableau

We consider the set of points $(i, p(i))$. This is called as the Viennot's geometric construction, where we reason about the graph. We will reason about the graph here, but couch the formal arguments in terms of partial orders to be precise.

At each point $(i, p(i))$, imagine a rectangle with $(i, p(i))$ as the lower left corner. Next, shine a flashlight from the point $(0, 0)$ towards the upper right quadrant; the boundary that is cast by the rectangles are called as the shadow lines.

Formally, we consider a dominance relationship where $(x, y) \lhd (p, q) \equiv x \leq p \land y \leq q$. Then, we get the "points on the shadow lines" by considering the Hasse diagram of the points $(i, p(i))$ under the relationship $\lhd$. Each level of the hasse diagram becomes one of the shadow lines. The collection of all of these shadow lines is called as the first order shadow lines.

Next, for each anti-chain, pick the element with the smallest $x$-coordinate. These points will form a chain. This chain will be first row of the permutation tableau $P$.

Funnily enough, it is also one of the longest increasing subsequences of the sequence $i \mapsto p(i)$ because the length of the longest chain (the longest increasing subsequence) is equal to the number of antichains (the number of shadow lines)

Duality theory of $\lhd$

Note that $\lhd$ as a relation is symmetric in $x$ and $y$. Thus, any order theoretic result we prove for $x$ will hold for $y$. But note that $(i, p(i))$ is the permutation $p$, while $(p(i), i)$ is the inverse permutation $(p^{-1})$. Thus, we should expect a "duality" between the order theoretic properties of $P$ and $p^{-1}$.

Djikstra's using a segtree

keep min segtree of distances. Now just have to run n-1 interations. You like segtrees right :P

Markov and chebyshev from a measure theoretic lens

I've been idly watching Probability and Stochastics for finance: NPTEL, and I came across this nice way to think about the markov and chebyshev inequality. I wonder whether Chernoff bounds also fall to this viewpoint.

Markov's inequality

In markov's inequality, we want to bound $P(X \geq A)$. Since we're in measure land, we have no way to directly access $P(\cdot)$. The best we can do is to integreate the constant function $1$, since the probability is "hidden inside" the measure. This makes us compute:

$$ P(X \geq A) \equiv = \int_{{X \geq A}} 1 d \mu $$

Hm, how to proceed? We can only attempt to replace the $1$ with the $X$ to get some non-trivial bound on $X$. But we know that $X \geq A$. so we should perhaps first introduce the $A$:

$$ P(X \geq A) \equiv = \int_{{X \geq A}} 1 d \mu = 1/A \int_{{X \geq A}} A d \mu $$

Now we are naturally led to see that this is always less than $X$:

$$ \begin{aligned} &P(X \geq A) \equiv = \int_{{X \geq A}} 1 d \mu = \ & 1/A \int{{X \geq A}} A d \mu < 1/A \int_{{X \geq A}} X d \mu = 1/A \mathbb{E}[X] \end{aligned} $$

This completes marov's inequality:

$$ P(X \geq A) \leq \mathbb{E}[X]/A $$

So we are "smearing" the indicator $1$ over the domain ${X \geq A}$ and attempting to get a bound.

Among any 51 integers, that are 2 with squares having equal value modulo 100

$1^n + 2^n + \dots + (n-1)^n$ is divisible by $n$ for odd $n$

$10^{3n+1}$ cannot be written as sum of two cubes

dual of applicative [WIP]

https://hackage.haskell.org/package/contravariant-1.5.3/docs/Data-Functor-Contravariant-Divisible.html

The dual of traversable [WIP]

https://hackage.haskell.org/package/distributive-0.6.2.1/docs/Data-Distributive.html

Coq-club: the meaning of a specification

When I was doing my PhD, I faced questions similar to yours. It emerged from my encounter of HOL4 for completing a project after having used Coq for another.

Given your question is on the meaning of a word, I would like to refer to a philosophical doctrine on how words acquire their meaning in a system of signs. Using that doctrine, I put forward how I came to an answer for myself!

So turns out that a text can be perceived as a construct made around elemental "oppositions". Accordingly, textual constructs only produce meaning through their interplay of DIFFERENCES (mostly emergingin in form of binary contrasts) inside a system of distinct signs. This doctrine was first introduced by Ferdinand Saussure on which J. Derrida drew for introducing his notion of difference.

Considering the above explanation, instead of hard wiring the words "specification" and "implementation" to predetermined functionality or referents, we can perceive them in a contrasting interplay whose connection is established via the proof game. The "specification" is something used by a "proof" to demonstrate "the correctness " of an "implementation ".

Now going for the Saussurian doctrine, there is no problem for an expression to be specification for an implementation, but itself being an implementation for something else. Therefore, I would definitely hesitate to say it is meaningless (or even misguiding) to use the word specification in the context of formal verification.

Hopefully that was useful!

• Link to coq-club discussion

SQLite opening

** The author disclaims copyright to this source code.  In place of
** a legal notice, here is a blessing:
**
**    May you do good and not evil.
**    May you find forgiveness for yourself and forgive others.
**    May you share freely, never taking more than you give.

Old school fonts

I've been rolling with the Px437 ToshibaSat 8x14 font as my daily driver purely for nostalgia reasons; It is to be honest quite a good font! Otherwise, I use Iosevka Fixed Expanded, or the "agda font", mononoki.

• I love the old school fonts website

Stalking syzigies on hackernews

He's the author of Macaulay; I learnt quite a bit by stalking him on hackernews

• Schreier–Sims algorithm for computing with permutations.

• Our phones should learn a private language with us. My dog learns after one repetition; Zoom should learn to arrange my windows as I like, at least after 47 repetitions.

• The bayer filter

• Our extrapolations always take the form of moving along a tangent vector out from prior experience. Prior to relativity, Newtonian physics was the belief that we actually lived in that tangent space. Surprises come when the deviations are large enough for reality to curve away from our models

• Like flipping through for the soft porn in a friend's "romance" novel, I must confess I searched straight for this guideline.

• Lisp's signature 17 car pileup at the end of every expression.

• I look for the $ or equivalent in any proposal out there, to see if the author has written lots of code or is just talking. It's like looking for bone marrow in beef stew, evaluating a cookbook. Marrow is central to the story of Lisp; we got our start being able to wield tools to crack open bones after lions and jackals had left a kill. The added nutrition allowed our brains to increase in size. Soon we mastered fire, then Lisp.

• I spent the first few months outside doing woodworking; I've been struggling with an overwhelming urge to center my consciousness in my hands. This is of course the history of our species, a biological urge as profound as our sex drive. We figured out how to make very sharp hunting tools from unruly rocks, or we died.

• spider webs on drugs

• The first chapter of Berstel and Reutenauer's "Noncommutative Rational Series with Applications" presents Schützenberger's theorem that every noncommuting rational power series is representable, and conversely. The idea is NOT painfully abstract, but makes twenty minutes work of a semester of undergraduate automata theory (an assertion I've tested multiple times in my math office hours).

• You don't want sync software going off and "thinking" about what a symlink really means, anymore than you'd want sync software going off and "thinking" after finding porn on your computer

• Luckily, I was trained far enough down the street from MIT to escape their Lisp world view, so we coded our computer algebra system in C, and it was fast enough to succeed and bring us tenure. Today, we'd choose Haskell.

His LISP language with inferred parens:

define | edge? g e
  let
    $ es | edges g
      e2 | reverse e
    or (member e es) (member e2 es)

(define (edge? g e)
  (let
    ( (es (edges g))
      (e2 (reverse e)))
    (or (member e es) (member e2 es))))

Conditional probability is neither causal nor temporal

I found this insightful:

P(A|B) means the probability of A happening given B already happened. Not so! P(A|B) doesn’t specify the time ordering of A and B. It specifies the order in which YOU learn about them happening. So P(A|B) is the probability of A given you know what happened with B.

This makes sense from the information theoretic perspective; I'd never meditated on this difference, though.

I'd seen things like:

P(sunrise | rooster-crow) = large even though rooster crowing does not cause the sunrise to happen.

but I'd never seen/actively contemplated an example of P(A|B) where they are temporally reversed/ambiguous.

Hook length formula

Truly remarkable formula that tells us the number of standard young tableaux for a given partition $\lambda$ of $n$. Recall the definitions:

• A partition $\lambda$ of the number $n$.
• An assignment of numbers ${1, 2, \dots n}$ onto the diagram of the partition such that the assignment is (a) weakly increasing in the rows, and (b) strictly increasing in the columns. It is strictly increasing in the columns because gravity acts downwards.
• Formally, a partition is written as $\lambda \equiv [\lambda_1, \lambda_2, \dots, \lambda_m]$, where $\lambda_i \geq 0$ and $\sum_i \lambda_i = n$, and that they are weakly decreasing ($\lambda_1 \geq \lambda_2 \geq \dots$).
• Formally, to define the tableaux, we first define the diagram $dg(\lambda) \equiv { (i, j) : 1 \leq j \leq \lambda[i] }$ which are the "locations" of the cells when visualizing $\lambda$ as a Ferrers diagram.
• Finally, the actual assignment of the numbers to the tableaux is given by a bijection $asgn: dg(\lambda) \rightarrow [n]$ such that $f$ is weakly increasing in the rows and strictly increasing in the columns.

The formula

Now, we want to count the number of young tableaux (formally, the data $n, \lambda, asgn$) for a given partition $\lambda$. The formula is:

$$ n!/\left(\prod_{\texttt{cell} \in \lambda} hooklen(\texttt{cell})\right) $$

where $hooklen$ is the largest "hook shape":

* * *
*
*
...

at the cell $(i, j)$ that is in the partition $\lambda$.

The structure of hooks

say we have a hook shape

a b c d
e
f

And the numbers ${1, 2, 3, 4, 5, 6}$. How many ways can we assign the numbers to the above hook shape such that its a legal young tableaux?

• First, see that $a = 1$ is a must. Proof by contradiction. Assume $1$ is not placed at $a$. Whenever it is placed, it will be less than the number placed at $1$. But this is wrong, because a young tableaux must be weakly increasing in the rows and strictly increasing in the columns.

• Next, see that after placing $a = 1$, the other numbers can be placed "freely": If we take a subset of ${2, 3, 4, 5, 6}$ of the size of the leftover row, ie, $|bcd| = 3$, then there is only one way to place them such that they are in ascending order. Similarly, the leftover numbers go to the column where there is only one way to place them.

• Hence, after $a = 1$ is fixed, for every $5C3$ subset, we get a legal hook.

• In general, if we have $n=r+c+1$ nodes, with $r+1$ nodes in the row, and $c+1$ nodes in the column (the top-left node is counted twice), then we have $\binom{r+c}{r}$ number of legal hooks; Once we pick the lowest number for the top left node, every $r$-subset will give us a hook.

• This result matches the hook-length formula. According to the hook length formula, we need to fill in for each node the length of the hook, and divide the full product by $n!$. So for the hook:

a b c d
e
f

This becomes:

6 3 2 1
2
1

$$ 6!/(6\times 3!\times 2!) = 5!/(3! 2!) = 5C3 = \binom{r+c}{r} $$

where $r=3, c=2$.

Knuth's heuristic

• Consider the hook shape. The only constraint we have is that the top-left number ought to be the smallest. For the hook $H$ to be legal, if we distribute numbers into it uniformly at random, then there is a $1/(\texttt{hook-length}(H))$ probability that the hook will be legal.

• The tableaux will be legal iff all the hooks in the tableaux are legal

• Thus, the probability of getting a legal tableaux is:

$$ \begin{aligned} &\texttt{num}(\lambda)/n! = \prod_{h \in \texttt{hook}(\lambda) 1/\texttt{hook-length}(h) \ &\texttt{num}(\lambda) = n!/\prod_{h \in \texttt{hook}(\lambda)\texttt{hook-length}(h) \ \end{aligned} $$

The relationship to representation theory

The RSK correspondence gives us a bijection between the permutation group $S_n$ and pairs of standard young tableaux:

$$ RSK \equiv \bigcup_{\lambda \in \texttt{partition}(n)} SYT(\lambda) \times SYT(\lambda) $$

given by the pair of insertion tableaux and the recording tableaux for each partition $\lambda$ of $n$.

If we look at this in terms of set sizes, then it tells us that:

$$ \begin{aligned} &|S_n| = |\bigcup_{\lambda \in \texttt{partition}(n)} SYT(\lambda) \times SYT(\lambda) \ &n! = \sum_{\lambda \in \texttt{partition}(n)} |SYT(\lambda)|^2 \ &n! = \sum_{\lambda \in \texttt{partition}(n)} |\texttt{hook-length-formula}(\lambda)|^2 \ \end{aligned} $$

This looks very suspicious, almost like the representation theoretic formula of:

$$ \texttt{group-size} = \sum_{\texttt{irrep} \in Repr(G)} dim(\texttt{irrep})^2 $$

and it is indeed true that $\texttt{hook-length-formula}(\lambda)$ corresponds to the dimension of an irreducible representation of $S_n$, and each $\lambda$ corresponds to an irrep of $S_n$.

The tyranny of light

More information may lead to less understanding; more information may undermine trust; and more information may make society less rationally governable.

Muirhead's inequality [WIP]

We denote by $\sum_! F(x[1], \dots, x[n])$ the sum ov $F$ evaluated over all permutations. Formally:

$$ \sum_! F(x[1], \dots, x[n]) \equiv \sum_{\sigma \in S_n} F(x[\sigma[1]], \dots, x[\sigma[n]]) $$

We write

$$ [a[1], \dots a[n]] \equiv 1/n! \sum_! x_1^{a[1]} \dots x[n]^{a[n]} = \sum_{\sigma \in S_n} \prod_{j} x[\sigma[j]]^{a[j]} $$

For example,we have:

• $[1, 1] = 1/2! (xy + yx) = xy$
• $[1, 1, 1] = xyz$
• $[2, 1, 0] = 1/3! (x^2y + x^2z + y^2z + y^2x + z^2x + z^2 y)$
• $[1, 0, 0] = 1/3! (x^{[1, 0, 0']} + x^{[1, 0', 0]} + x^{[0, 1, 0']} + x^{[0', 1, 0]} + x^{[0, 0', 1]} + x^{[0', 0, 1]})$. This is equal to $2!(x + y + z)/3! = (x + y + z)/3$.
• In general, $[1, 0, 0, 0, \dots, 0]$ ($n$ zeroes) is $(n-1)!/n!(\sum_i x_i)$ which is the AM.
• Also, $[1/2, 1/2] = 1/2!(x^{1/2}y^{1/2} + y^{1/2}x^{1/2}) = \sqrt{xy}$.
• In general, $[1/n, 1/n, \dots, 1/n]$ is the GM $\sqrt{n}{x[1] x[2] \dots x[n]}$.

Majorization

Let $(a), (b) \in \mathbb R^n$ be two non-decreasing sequences: $a[1] \geq a[2] \dots \geq a[n]$, and $b[1] \geq b[2] \dots \geq b[n]$. We will say that $(b)$ is majorized by $(a)$ (written as $(b) \prec (a)$) when we have that:

1. $a[1] \geq a[2] \geq \dots a[n]$, $b[1] \geq b[2] \geq \dots b[n]$.
2. $\sum_i b[i] = \sum_i a[i]$.
3. $\sum_{i=1}^u b[i] \leq \sum_{i=1}^u a[i]$ for $1 \leq i \leq n$.

It is clear that this is a partial order. The below figure shows majorization in terms of partitions. For two sequences $f, g$, define $F$ to be their "integral" (partial sums) and $f', g'$ to be their "derivatives" (finite differences). Then the condition that $f \prec g$ states that $F$ is upper bounded by $G$, and that $F, G$ are concave functions.

The other lens of viewing majorization is to think of a number as some sort of fixed length $l$, and we are allowed to make some progress to reach the goal ($f(x) > 0$) as long as we progress less at each each timestep ($f''(x) < 0$). In this viewpoint, the majorization condition asserts that $f \prec g$ is that $g$ will always be ahead of/not fall behind $f$.

Majorization and step

We can show that if $(b) \prec (a)$ , then we can get from $(b)$ to $(a)$ in a finite number of discrete steps, that "borrow" from higherlocations in $b$ and "give" to lower locations. Formally, define a step operator $S(l, r)$ where $l < r$ such that:

$$ S(l, r)(b)[k] = \begin{cases} b[l]+1 & k = l \ b[r]-1 & k = r \ b[k] & \texttt{otherwise} \end{cases} $$

That is, this borrows a single value from $b[j]$ and gives it to $b[i]$. We can see that $(b) \prec S(l, r)(b)$.

For a given $(b) \prec (a)$, we can find a sequence of step operations $S(l[i], r[i])$ such that we transform $(b)$ into $(a)$; That is, it is possible to "single-step" the translation from $(b)$ to $(a)$.

Muirhead's theorem statement

for non negative numbers $x[]$, we have:

$$[b] \leq [a] \iff (b) \prec (a)$$

Expanding it out, this means that:

$$ 1/n! \sum_! x^{[b]} \leq 1/n! \sum_! x^{[a]} \iff (b) \prec (a) \ \sum_! x^{[b]} \leq \sum_! x^{[a]} \iff (b) \prec (a) \ $$

Rearrangement inequality

If $a[i]$ is a non-decreasing sequence: $a[1] \leq a[2] \leq \dots a[n]$, and similarly $b[i]$ is a non-decreasing sequence: $b[1] \leq b[2] \leq b[n]$ then we have that:

$$ \sum_i a[i] b[i] \geq \sum_i a[\sigma[i] b[i] $$

for any permutation $\sigma \in S_n$.

insight: the greedy strategy is the best. Think of $b[n]$ as the max. number of times we are allowed to pick some $a[i]$. It is best to be greedy and pick the value $\max_i a[i]$ $b[n]$ number of times. $\max_i a[i] = a[n]$. Thus having $a[n]b[n]$ will beat all others.

Proof

The proof strategy is to: show what happens for a transposition. Every permutation can be broken down into transpositions and thus we are done.

Let $S = \sum_i a[i] b[i]$. Let $T$ be $S$ with us picking the value $a[r]$ $b[s]$ times, and picking the value $a[s]$ $b[r]$ times. This gives

$$ T = \sum_{i \neq r, s} a[i] b[i] + a[r]b[s] + a[s]b[r] $$

Since we wish to show $S > T$, let's consider $S - T$:

$$ \begin{aligned} &S - T = \sum_i a[i]b[i] - (\sum_{i \neq r, s} a[i]b[i] + a[r]b[s] + a[s]b[r]) \ &=\sum_{i \neq r, s} a[i]b[i] + a[r]b[r] + a[s]b[s] - (\sum_{i \neq r, s} a[i]b[i] + a[r]b[s] + a[s]b[r]) \ &= a[r]b[r] + a[s]b[s] - a[r]b[s] - a[s]b[r] \ &= a[r](b[r] - b[s]) + a[s](b[s] - b[r]) \ &= a[r](b[r] - b[s]) - a[s](b[r] - b[s]) \ &= (a[r] - a[s])(b[r] - b[s]) \end{aligned} $$

Since $r < s$ we have $b[r] \leq b[s]$, hence $b[r] \leq b[s] < 0$. For the product to be greater than zero, we need $a[r] \leq a[s]$, or $a[s] \geq a[r]$ when $s > r$.

Hence, for a transposition, we are done. Thus we are immediately done for any permutation:

Application: AM-GM

Say we wish to show $(p + q)/2 \geq \sqrt{pq}$. Let WLOG $p \leq q$. Pick the sequences:

$$ a = [p, q]; a' = [q, p]; b = [p, q] $$

Then the rearrangement inequality gives us:

$$ \begin{aligned} &a[1]b[1] + a[2]b[2] \geq a'[1]b[1] + a'[2]b[2] \ &p^2 + q^2 \geq qp + pq \ &(p^2 + q^2)/2 \geq pq \end{aligned} $$

Pick $p = \sqrt{r}, q = \sqrt{s}$ to arrive at:

$$ (r + s)/2 \geq \sqrt{rs} $$

and thus we are done.

References

• Inequalities: a mathematical olympiad approach

Triangle inequality

We can write this as:

   *A
 b/ |
C*  | 
 a\ | c
   *B

The classical version one learns in school: $$ c \leq a + b $$

The lower bound version:

$$ |a - b| \leq c $$

This is intuitive because the large value for $a - b$ is attained when $b = 0$. (since lengths are non-negative, we have $b \geq 0$. if $b = 0$, then the point $A = C$ and thus $a = CB = AB = c$.

A/C (b=0)
|
| a=c
|
B

Otherwise, $b$ will have some length that will cover $a$ (at worst), or cancel $a$ (at best). The two cases are something like:

 A
 ||b
 ||
c|*C
 ||a
 ||
 ||
 B

In this case, it's clear that $a - b < c$ (since $a < c$) and $a + b = c$. In the other case, we will have:

 C
b||
 ||
 A|
 ||
 ||a
c||
 ||
 ||
 ||
 B

Where we get $a - b = c$, and $c < a + b$. These are the extremes when the triangle has zero thickness. In general, because the points are spread out, when we project everything on the $AB=c$ line, we will get less-than(<=) instead of equals (=).

The Heather subculture

• And finally, the sweater's perspective

Frobenius Kernel

Some facts about conjugates of a subgroup

Let $H$ be a subgroup of $G$. Define $H_g \equiv { g h g^{-1} : h \in H }$.

• We will always have $e \in H_g$ since $geg^{-1} = e \in H_g$.
• Pick $k_1 k_2 \in H_g$. This gives us $k_i = gh_ig^{-1}$. So, $k_1 k_2 = g h_1 g^{-1} g h_2 g^{-1} = g (h_1 h_2) g^{-1} \in H_g$.
• Thus, the conjugates of a subgroup is going to be another subgroup that has nontrivial intersection with the original subgroup.
• For inverse, send $k = ghg^{-1}$ to $k^{-1} = g h^{-1} g^{-1}$.

Frobenius groups

Galois theory by "Abel's theorem in problems and solutions"

I found the ideas in the book fascinating. The rough idea was:

• Show that the $n$th root operation allows for some "winding behaviour" on the complex plane.
• This winding behaviour of the $n$th root is controlled by $S_n$, since we are controlling how the different sheets of the riemann surface can be permuted.
• Show that by taking an $n$th root, we are only creating solvable groups.
• Show tha $S_5$ is not solvable.

Galois theory perspective of the quadratic equation

I found this quite delightful the first time I saw it, so I wanted to record it ever since.

Let $x^2 + bx + c$ be a quadratic. Now to apply galois theory, we first equate it to the roots:

$$ \begin{aligned} &x^2 + bx + c = (x - p)(x-q) &x^2 + bx + c = x^2 - x(p + q) + pq &-(p + q) = b; pq = c \end{aligned} $$

We want to extract the values of $b$ and $c$ from this. To do so, consider the symmetric functions:

$$ (p + q)^2 = b^2 (p - q)^2 = (p + q)^2 - 4pq = b^2 - 4c $$

Hence we get that

$$ p - q = \pm\sqrt{b^2 - 4c} $$

From this, we can solve for $p, q$, giving us:

$$ p = ((p + q) + (p - q))/2 = (-b \pm \sqrt{b^2 - 4c})/2 $$

Galois theory for cubics

Galois theory for bi-quadratics

Galois theory for quintics

References

• Abel and the insolubility of the quintic

Burnside lemma by representation theory.

Recall that burnside asks us to show that given a group $G$ acting on a set $S$, we have that the average of the local fixed points $1/|G|(\sum_{g \in G} |\texttt{Fix}(g)|)$ is equal to the number of orbits (global fixed points) of $S$, $|S/G|$.

Let us write elements of $g$ as acting on the vector space $V_S$, which is a complex vector space spanned by basis vector ${ v_s : s \in S }$. Let this representation of $G$ be called $\rho$.

Now see that the right hand side is equal to

$$ \begin{aligned} &1/|G| (\sum_g \in G Tr(\rho(g))) \ &= 1/|G| (\sum_g \in G \chi_\rho(g) ) \ &\chi \rho \cdot \chi_1 \end{aligned} $$

Where we have:

• $\chi_1$ is the charcter of the trivial representation $g \mapsto 1$
• The inner product $\langle \cdot , \cdot \rangle$ is the $G$-average inner product over $G$-functions $G \rightarrow \mathbb C$:

$$ \langle f , f' \rangle \equiv \sum_{g \in G} f(g) \overline{f'(g)} $$

So, we need to show that the number of orbits $|S/G|$ is equal to the multiplicity of the trivial representation $1$ in the current representation $\rho$, given by the inner product of their characters $\chi_1 \cdot \chi_\rho$.

let $s* in S$ whose orbit we wish to inspect. Build the subspace spanned by the vector $v[s*] \equiv \sum_{g \in G} \rho(g) v[s]$. This is invariant under $G$ and is 1-dimensional. Hence, it corresponds to a 1D subrepresentation for all the elements in the orbit of $s*$. (TODO: why is it the trivial representation?)

Contributing to SAGEmath

Development

• The first time, run make build. DO NOT RUN make, as this performs a make doc as well which burns cycles building docs for no reason.

• Normally, if you just change Python code in the library, it suffices to run ./sage -br to update Python.

• Only if you changed docs, and want to test that they still work, you'd need to run make, or make doc-html

• To run doctests, can run ./sage -t <filepath>. More info on the sage doctesting page

• make build && ./sage -n=jupyter ./test-ddg-notebook.ipynb is reasonably fast.

• SAGE developer index

• Baby's first Trac ticket: #31248 --- Make tableaux error messages more precise

Git the hard way for SAGE

• Git the hard way

git with SAGE uses different URLs for fetch and push.

[[email protected] sage]$ git remote add trac git://trac.sagemath.org/sage.git -t master
[[email protected] sage]$ git remote set-url --push trac [email protected]:sage.git
trac        git://trac.sagemath.org/sage.git (fetch)
trac        [email protected]:sage.git (push)

• I use my github account to develop for SAGE.
• Linking your SSH key with sage-trac

Getting the commit merged

The release manager (Volker Braun) takes care of it. A number of people can close tickets for invalidity/duplicate etc, but the actual merging is done by one person only (and a number of bots/scripts that help).

A positively reviewed ticket with green bots and all fields filled in will usually be merged in a week or two or rejected (merge conflict, issues with specific architectures, failing bots). But it might take longer (too many positively review tickets waiting, end of release cycle).

Tending to the garden

• Fix typos
• Fix pep8, pyflakes, lint warnings. Try to simplify code that's marked very compliated by radon.
• Fix code that's marked by lgtm

Shadow puppet analogy for entanglement

I found this answer on quantumcomputing.stackexchange to be a visceral example of "something like entanglement":

Imagine making shadow puppets. However in this setup, instead of one you have two screens and two torches pointing 90 degrees apart so that the image formed by torch 1 is projected onto screen 2 and the image formed by torch 2 is simultaneously projected onto screen 1.

 screen 1       screen 2
   /               \
  /                 \
 /                   \
          mm              <-  hand
      \         /
   torch 1   torch 2

Now any movement of your hand changes both images in a correlated way. In a sense, the images are entangled - if you observe image 1 to have a certain configuration, then only a small subset of possibilities in the total configuration space of image 2 are valid, and vice versa.

Books for contest math

A personal list of books I wish to study this year, to get better at "problem solving". This is ranked in order of difficulty I wish to spend this year learning nuts and bolts type things.

• Inequalities: an olympid approach --- Nice book, has an axiomatic/algebraic bent.
• Mathematical circles: Russian experience
• The art and craft of problem solving
• Basics of Olympiad Inequalities: Samin Riasat --- quickly covers the big 12.
• Evan chen: A Brief Introduction to Olympiad Inequalities
• Pham Kim Hung: Secrets in Inequalities
• Edwin Beckenback: Introduction to Inequalities
• Nicholas D. Kazarinoff : Geometric inequalities
• Introduction to Functional Equations: Theory and problem-solving strategies for mathematical competitions and beyond
• Combinatorics: Introduction to counting and probability
• Combinatorics: Intermediate counting and probability
• Algebra: 101 Problems in Algebra by Titu Andreescu
• Number Theory Structures, Examples and Problems
• Combinatorics: 102 Combinatorial problems
• Combinatorics: Pablo Soberon’s Problem Solving Methods in Combinatorics
• Geometry: Yufi Zhao: handouts
• Geometry: Trig bashing / Barycentric bashing (evan cheng)
• Problem-solving Strategies In Mathematics: From Common Approaches To Exemplary Strategies
• Problems from the Book
• Straight From the Book
• AoPS list of past problems
• AoPS list of books
• Mathematical problem solving: MIT course

Analysing simple games

I found the clear articulation of these ideas quite nice.

1. In a game with symmetry, a symmetric move can be blocked or prevented only by the previous move an opponent has just made.
2. The symmetry in many games can be written as some kind of equality, where at each turn, one first player breaks the symmetry, and the other player (who has the winning strategy) restores it.

Example game

Consider a game where two players take turns placing bishops on a chessboard, so that the pieces cannot capture each other. The player who cannot win loses.

Winning strategy

place the bishop symmetrically about the line passing between the fourth and fifth column (file). Note that the only way this bishop could be blocked is if the move just made by the other player can block it.

References

• Mathematical circles: Russian experience

Using the bound library (WIP)

Linear algebraic proof of the handshaking lemma

We wish to show that the number odd vertices is even. Let $A$ be the adjacency matrix of the undirected graph $G$. Since $G$ is undirected, $A = A^T$. Now move everything to $F_2$, including $A$. This means that $A$ has entries ${0, 1}$. Now, denote the vector of all ones by $o \equiv (1, 1, \dots 1)$. See that $Ao$ counts the partities of the degrees of each vertex, and $o^T(Ao)$ counts the sum of parities of the degrees of each vertex.

Note that the vertices of even degree with add $0$ to the sum $o^TAo$, while odd vertices will add a $1$. Thus, $o^TAo$ will equal the parity of the number of odd vertices. As we wish to show that the number of odd vertices is even, we want to prove that $o^TAo = 0$.

We will now algebraically simplify $o^TAo$ (does anyone have a cleaner proof?) giving us:

$$ \begin{aligned} &o^TAo = \sum_{ij} o_i A_{ij} o_j \ &= \sum_{i=j} o_i A_{ij} o_j + \sum_{i < j} o_i A_{ij} o_j + o_j A_{ji} o_i \ &\text{($A$ is symmetric; $A_{ji} = A_{ij}$)} \ &= \sum_{i=j} o_i A_{ij} o_j + \sum_{i < j} o_i A_{ij} o_j + o_j A_{ij} o_i \ &= \sum_{i=j} o_i A_{ij} o_j + \sum_{i < j} 2 \cdot o_i A_{ij} o_j \ &\text{($F_2$ has characteristic zero, so $2 = 0$)} \ &= \sum_{i=j} o_i A_{ij} o_j + 0 \ &\text{(replace $i = j$ with $k$)} \ &= \sum_{k} o_k A_{kk} o_k \ &\text{($A_{kk} = 0$ since graph has no self loops)} \ &= \sum_{k} 0 \cdot o_k^2 = 0 \end{aligned} $$

So, the number of vertices of odd degree is even.

I want to avoid this computation with respect to the basis, but I'm not sure how to do that.

A simplification from arjun

Since $A_{kk} = 0$, we have that $A = B + B^T$ for $B$ lower triangular. This allows us to simplify:

\begin{aligned} & o^T A o = o^T (B + B^T) o = \ & =o^T B o + o^T B^T o = \langle o, Bo \rangle + \langle Bo, o \rangle \ & = 2 \cdot \langle o, Bo \rangle = 0 \end{aligned}

Historical contemporaries

I continue to be delighted at how connected arbitrary parts of history are. Here's a list of contemporaries I would not have guessed:

• Rembrandt sketched Shah jahan
• Greek ambassador in the Ashoka court
• "Bhaeatha's kingdom" for Bharat as known by the Chinese
• Aurangzeb had rockets when fighting his brother
• Aurangzeb had a French physician (Francois bernier)
• Picasso was against the Korean war (1950) and painted about it.

Rota's twelvefold way

• Count functions from $I \rightarrow O$.
• See that any such function is a subset of $O^I$.
• We can write such a function as $(o_1, o_2, \dots, o_{|I|}) \in O^I$
• if we have $S_I \circ f$, this means that we can permute images.
• If we have $f \circ S_O$, this means that we can permute fibers.

f any function

• we count $O^I$

f injective

• We count $O^{(I)} = O(O-1)\dots(O-I+1)$ as given by the falling factorial.

f surjective, with equivalence $S_I \circ f$.

• For each element $o \in O$, pick some subset $I_o \subseteq I$. We need the subsets $I_o$ to be disjoint, and all $I_o$ to be non-empty.
• We can permute the fibers $I_o$, so we can place them by weakly decreasing order of size.
• Then this is the same as counting partitions of $I$ into $O$ subsets, given by $S(n, x)$/${n\brace m}$ (stirling numbers of the second kind).

f surjective

• For each element $o \in O$, pick some subset $I_o \subseteq I$. We need the subsets $I_o$ to be disjoint, and all $I_o$ to be non-empty.
• We get partway there by counting compositions of $I$: the number of ways to split $|I|$ into $(a_1, a_2, \dots, a_k)$ such that each $(a_i > 0)$ and $\sum_i a_i = |I|$. Note that ordering matters here, since we write a tuple $(a_1, a_2, \dots a_k)$.
• For example, the compositions of $3$ are $(1, 1, 1)$, $(1, 2)$ and $(2, 1)$. See that we have both $(1, 2)$ and $(2, 1)$.
• Contrast this with partitions, which I write in weakly decreasing: $(1, 1, 1)$, $(2, 1)$.
• This can be counted by the stars and bars method:

1 _ 2 _ 3 _ 4 _ ... _  |I|

• We want to fill the $|I|-1$ blanks (_) with $k$ bars if we want a $k$-composition (remember that compositions can't have zeros). So we can count this by $\binom{|I|-1}{k}$.

f surjective, with equivalence $S_I \circ f \circ S_O$:

Counting necklackes with unique elements

Count number of ways to form a necklace with ${1, 2, \dots, n}$

• Method 1: This is equivalent to counting $|S_5|$ modulo the subgroup generated by $(12\dots)$. That subgroup has size $5$. So the size is $S_5/5$.
• Method 2: A cycle is an equivalence class of elements $(a,b,c,d,e)$ along with all of its cyclic shifts ($(b,c,d,e,a)$, $(c,d,e,a,b)$, $(d,e,a,b,c)$, $(e,a,b,c,d)$). We are to count the number of equivalence classes. First pick a canonical element of each equivalence class of the form $(1, p, q, r, s)$.

Decomposition of projective space

Projective space $\mathbb P^{n+1} = \mathbb P^n \cup \mathbb R^n$. The current way I think about this is as follows (specialize to $n=3$)

• Consider a generic point $[x : y : z]$. Either $x = 0$ or $x \neq 0$.
• If $x = 0$, then we have $[0 : y : z]$ which can be rescaled freely: $[0: y: z] = (0, y, z, 1) = (0, \lambda y, \lambda z, \lambda) = [0: y: z]$. So, we get a component of $\mathbb P^2$ from the $[y: z]$.
• If $x \neq 1$, we have $[x : y : z]$. Spend the projectivity to get $(1:y:z) = (x, y, z, x)$. Now we have two free parameters, $(y, z) \in \mathbb{R^2}$. This gives us the $\mathbb R^2$.

There's something awkward about this whole thing, notationally speaking. Is there a more natural way to show that we have spent the projectivity to renormalize $[x: y: z]$ to $(1, y, z)$ ?

Projective plane in terms of incidence

We can define $\mathbb P^2$ to be an object such that:

1. Any two lines are incident at a single point.
2. Two distinct points must be incident to a single line. (dual of (1))

The points at infinity

This will give us a copy of $\mathbb R^2$, along with "extra points" for parallel lines.

• Consider two parallel lines $y = mx + 0$ and $y = mx + 1$. These don't traditionally meet, so let's create a point at infinty for them, called $P_m(0, 1)$.

• Now consider two more parallel lines, $y = mx + 0$ and $y = mx + 2$. These don't traditionally meet either, so let's create a point at infinite for them, called $P_m(0, 2)$.

• Finally, create another point $P_m(0, 3)$ as the point of intersection between $y = mx + 0$ and $y = mx + 3$.

• Now, consider $P_m(0, 1), P_m(0, 2), P_m(0, 3), dots$. We claim that they must all be equivalent. Assume not. Say that $P_m(0, 1) \neq P_m(0, 2)$.

• Then there must a line that joins $P_m(0, 1)$ an $P_m(0, 2)$. Call it $L_m(0, 1, 2)$. Now, what is the intersection between $L_m(0, 1, 2)$ and the line $y = mx + 0$? The points $P_m(0, 1)$ and $P_m(0, 2)$ both lie on the line $L_m(0, 1, 2)$. But this is a contradiction: two lines must be incident at a single unique point.

• So we must have $P_m(0, 1) = P_m(0, 2) = P_m$. So, for each direction, we must have a unique point where all lines in that direction meet.

We can make a definition: the point at infinity for a given direction is the equivalence class of all lines in that direction.

The line at infinity

This now begs the question: what lines to different points at infinity lie on? Let's consider $P_q, P_r, P_s, P_t$ as four points at infinity for four different slopes.

• Consider the lines $L(q, r)$ that is incident on $P_q$ and $P_r$, and then the line $L(s, t)$ that is incident on the lines $P_s$ and $P_t$.
• This begs the question: where do these lines meet? If we say that the meet at more new points of intersection, like $P(q, r, s, t)$ this process will never end.
• So we demand that all points at infinity lie on a unique line at infinity.

Childhood: Playing pokemon gold in japanese

I just recalled this very off memory of how back when I was a kid, somehow the only version of pokemon (gold) that was circulating amongst folks was the one in japanese. So we freaking played gold in japanese. I can't believe I got through so many levels with no clue of what in the actual fuck I was doing. I remember being stuck at the point where you need to use cut to cross a barrier or something, and figuring it out by accident.

Pretty sure I got blocked someplace because I lost the surf HM.

This memory just resurfaced, and I spent a solid five minutes thinking about just how insane the whole thing is. A kid's determination to play a game knows no bounds, indeed.

Tensor is a thing that transforms like a tensor

There are two ways of using linear maps in the context of physics. One is as a thing that acts on the space. The other is a thing that acts on the coordinates.

So when we talk about transformations in tensor analysis, we're talking about coordinate transformatios, not space transformations.

Tensor Hom adjunction

• (- X A) witnesses A as an output, while Hom(A, -) witness A as input.
• Similarly, we know that we can contract A with A* so it makes sense that the "dual" of multiplying by A (ie, how to divide out A) is to invert it by allowing a contraction with A*.

Schur's lemma

Statement

if $r_v : G \rightarrow GL(V), r_w: G \rightarrow GL(W)$ are two irreducible representations of the group $G$, and $f: V \rightarrow W$ is an equivariant map (that is, $f\forall g \in G, \forall v \in V, (r_v(g)(v)) = r_w(g)(f(v))$), then we have that either $f = 0$ or $f$ is an isomorphism.

• Said differently, this implies that either $r_v$ and $r_w$ are equivalent, and $f$ witnesses this isomorphism, or $V$ and $W$ are not isomorphic and $f$ is the zero map.

Proof

• First, note that $ker(f)$ and $im(f)$ are invariant subspaces of $G$.
• Let $k \in ker(f)$. hence:

$$ \begin{aligned} &r_w(g)(f(k)) = 0 \ &f(r_v(g)(k) = r_w(g)(f(k)) = 0 \ &r_v(g)(k) \in ker(f) \ \end{aligned} $$ So if $k \in ker(f)$ then so does $r_v(g)(k)$ for all $g$. Hence, the kernel is an invariant subspace.

• Next, let $w \in im(f)$, such that $w = f(v)$ hence:

$$ \begin{aligned} &f(v) = w \ &r_w(g)(w) = r_w(g)(f(v)) = f(r_v(g)(v)) \ &r_w(g)(w) \in im(f) \ \end{aligned} $$

So if $w \in im(f)$ then $r_w(g)(w) \in im(f)$ for all $g$. Hence, image is an invariant subspace.

• Since $V$ is irreducible, we must have that either $ker(f) = 0$ or $ker(f) = V$. If this were not the case, then we could write $V = ker(f) \oplus ker(f)^\perp$ non-trivially. This contradicts the irreducible nature of $V$. Thus, either $f$ sends all of $V$ to $0$ (ie, $f$ is the zero map), or $f$ has trivial kernel (ie, $f$ is injective).
• Since $W$ is irreducible, we must have that either $im(f) = 0$ or $im(f) = W$ by the exact same argument; $im(f)$ is an invariant subspace, and $W$ is irreducible thus has non non-trivial invariant subspaces. Thus either $im(f) = 0$ ($f$ is the zero map), or $im(f) = W$ ($f$ is surjective).
• Thus, either $f$ is the zero map, or $f$ is both injective and surjective; that is, it is bijective.
• The real star of the show is that (1) we choose irreducible representations, and (2) kernel and image are invariant subspaces for the chosen representations, thus we are forced to get trivial/full kernel/image.

Strengthing the theorem: what is $f$?

We can additionally show that if $f$ is not the zero map, then $f$ is constant times the identity. That is, there exists a $\lambda$ such that $f = \lambda I$.

• $f$ cannot have two eigenvalues. If it did, the eigenspaces of $\lambda_1$ and $lambda_2$ would be different subspaces that are stabilized by $f$. This can't happen because $V$ is irreducible. So, $f$ has a single eigenvalue $\lambda$.
• Thus, if $f$ has full spectrum, it's going to be $f = \lambda I$.
• $f$ has full spectrum since we tacitly assume the underlying field is $\mathbb C$ and $f$ has full rank.

Newton polygon and simplification, blowing up (WIP)

• Borcherds

Daughters of destiny

Captures the microcosm of what it means to live in India.

• Shanti Bhavan

Stuff I learnt in 2020

• MLIR
• unification
• GRIN
• demand analysis
• tabled typeclass resolution
• ZX
• pwn.college
• semantics of general relativity
• mathemagic
• oripa and FOLD
• tensegrity
• uncivilization
• CSES
• USACO
• rete
• number theory / amalgam
• sampleraytracer
• bijective combinatorics
• Why do people stay poor?
• Talk: p-adics
• Talk: smallpt-hs

Method of types in information theory(WIP)

Line bundles, a high level view as I understand them today

• What is a line bundle?
• What does it mean to tensor two line bundles?
• Why are line bundles invertible?
• Can we draw pictures?

Why are bundles invertible?

Because locally, they're locally modules. This leads us to

Why are modules invertible?

All modules are invertible when tensored with their dual.

To simplify further, let's move to linear algbera from ring theory; consider the field $\mathbb R$. Over this, we have a vector space of dimension $1$, $\mathbb R$. Now, if we consider $\mathbb R \otimes \mathbb R^*$, this is isomorphic to $\mathbb R$ since we can replace $(r, f) \mapsto f(r)$. This amounts to the fact that we can contract tensors.

So, $\mathbb R \otimes \mathbb R^* \simeq \mathbb R$. Generalize to bundles.

References

• Fiber bundles at physics travel guide

Conversations with a wood carver

There's a wood carver who lives close to home, whose name is Harish. I went to speak to him, asking if he would be willing to teach me woodcarving. It was a very interesting converstaion.

• He argued that wood carving was his caste, and it was impossible for him to teach me this, since he learnt it "by practice from birth".
• He also mentioned that his skills were learnt by practice, and not through training and were thus un-teachable.
• He felt that it was impossible to pick up the skill anymore since I ddn't learn it as a kid.
• His feeling is that the art of wood carving is not respected, and it makes much more sense to go learn how to use a CNC .
• We spoke about how the traditional style of woodcarving provided more control, and led to better construction. He said that consumers don't care, and resent him for the extra time.
• He oft repeated how he was poor; He wakes up in the morning, takes care of his cows, then begins carving. He might stay up late if there's an urgent order.
• None of his children learnt woodcarving either. They seem to be learning things like commerce and graphic design. It seems likely that woodcarving will die with him.
• He also mentioned how he no longer carves for the local temples, who one would expect would be his largest customer base since he specializes in carving paraphranelia for idols. It turns out that temples only provide "blessings", and no payment.
• When carving beds for gods, one must arrange the bed to be along the natural direction of the tree. The feed of the god must be in the direction of the roots, and the head must be towards the sky. Otherwise, the god will not accept the tree.
• Towards this, there are many interesting principles of how to learn the direction of wood.
• For one, one can use knots in the wood to identify the direction of growth. See the knot in the front and back of a block of wood. There will be a directionality to this knot. See that branches grow from low to high; So the knot indicates the direction of growth of the tree.
• For another, we can cut a think horizontal slice from the block of wood. In the two halves, the splinters will "point upwards" in the slice.

In general, this conversation left me quite dejected about the state of arts in India. It seems like traditional carpentry in India is dead, and the "replacements" are of terrible quality. I was also saddened that he so adamantly believes that it is fundamentally impossible for people to learn carpentry.

Resolution and first order logic (WIP)

• Stanford intro to logic

Kruskal card trick (WIP)

Discrete Riemann Roch (WIP)

Divisors

Function $V \rightarrow \mathbb Z$. We think of this as formal linear combination of vertices.

Degree of a divisor

$deg(D) \equiv \sum_{v \in V} D(v)$.

Borrowing and lending at a vertex $v_\star$

• Lending: $v$ gives 1 unit of money to all its neighbours

$$ f' = f + \sum_{vw \in E} -v + w $$

• Borrowing: $v$ takes 1 unit of money from all its neighbours

$$ f' = f + \sum_{vw \in E} + v - w $$

Borrowing and lending on a set $S$:

• Lending on a set $S$: every vertex $v \in S$ gives 1 unit of money to all its neighbours

$$ f' = f + \sum_{v \in S}\sum_{vw \in E} -v + w $$

• Borrowing defined similarly.
• See that borrowing at a vertex $v$ is the same as lending from $V / v$. The reason being, the lending between vertices of $V/v$ will cancel, and only lends into $v$ will be counted. This is the same as $v$ borrowing.

Linear equvivalence

Two divisors $D_1, D_2$ are linearly equivalent iff there is a sequence of borrowing or lending moves that leads from $D_1$ to $D_2$. This is an equivalence relation on the space of divisors. Equivalence class of $D_1$ is represented by $[D_1]$.

Partial ordering of divisors

We say that $D_1 < D_2$ if for all $v$, $D_1(v) < D_2(v)$.

Effective divisors

A divisor such that $\forall v, D(v) \geq 0$ is called as an effective divisor. Sometimes written as $D \geq 0$.

Our goal is given a divisor $D$, to check if it is linearly equivalent to a divisor $D'$ such that $D \geq 0$. If we can do so, then no one is in debt, and we have won the game.

Addition of divisors

We add divisors pointwise: $(f + g)(v) \equiv f(v) + g(v)$. This respects linear equivalence. Hence, $[D_1] + [D_2] \equiv [D_1 + D_2]$. This makes divisors, and their equivalence classes an abelian group

The Picard Class Group (group of divisor classes)

The group of equivalence classes of divisors under pointwise addition is the picard group.

Jacobian Class group (divisor classes of degree 0).

• Subgroup of picard group of degree 0.
• That is, all equivalence class elements of degree 0.
• This is well defined because all linearly equivalent divisors (divisors that can be gotten by lending/borrowing) all have the same degree (total money). This is because lending/borrowing does not change the total amount of money in the market, only redistributes it.

Picard group decomposition in terms of Jacobian group

For each $q \in V$, there is an isomorphism of groups $\phi_q: Pic(G) \rightarrow \mathbb Z \times Jac(G)$, where we send a divisor class $[D]$ to $\phi_q([D]) \equiv (deg(D), [D - deg(D)q]$.

• Clearly, the new divisor $[D - deg(D)q]$ has total degree $0$, since $deg(D)$ has been subtracted off at $q$.
• We can recover the original divisor since we know $deg(D)$.

Complete linear system $[D]_{\geq 0}|$

The complete linear system of $D$ is the set of all winning configurations from $D$. That is:

$$ [D]_{\geq 0} \equiv { E \in [D] : E \geq 0 } $$

We win the game if $[D]_{\geq 0}$ is nonempty.

The discrete laplacian

The laplacian is the map $L: (V \rightarrow \mathbb Z) \rightarrow (V \rightarrow \mathbb Z)$ defined by:

$$ L(f)(v) \equiv \sum_{vw \in E} (f(v) - f(w)) $$

That is, $L(f)(v)$ is the total deviation of $v$ from all of its neighbours $w$.

Firing script

A firing script is a function $s: V \rightarrow \mathbb Z$ ($s$ for script) that tells us how many times $v$ lends money to its neighbours).

• The collection of all firing scripts form an abelian group, and is denoted by $M(G)$. [TODO: why $M$?]

• Set lending by a subset $W \subset V$ is denoted by $\chi_W$, where $\chi_W(v) \equiv 1$ if $v \in W$ and $\chi_W(v) \equiv 0$ otherwise. Written in iverson notation, we have $\chi_W(v) \equiv [v \in_? W]$.

• The effect of running a firing script $s$ on a divisor $D$ to get a divisor $D'$ is:

$$ \begin{aligned} D' \equiv D + \sum_{v \in V} s(v) (-v+ w) \ \end{aligned} $$

if $s: V \rightarrow \mathbb Z$ is a firing script, then the divisor of the firing script $s$ is:

$$ div(s) \equiv \sum_{v \in V} s(v) (-v+ w) $$

• The effect of running a firing script is to replace a divisor $D$ by a new divisor $D' = D + div(s)$. We denote this by $D \xrightarrow{s} D'$ and call this as script-firing

div is a group homomorphism

We see that div is a function from $M(G) = V \rightarrow \Z$ to $Div(G) = V \rightarrow \Z$ under the map:

$$ div(s) \equiv \sum_{v \in V} s(v) (-v+ w) $$

We show that $div(s_1 - s_2) = div(s_1) - div(s_2)$ thereby checking the homomorphism property.

$$ \begin{aligned} &div(s_1 - s_2) = \sum_{v \in V} (s_1 - s_2)(v) (-v+ w) \ &= \sum_{v \in V} (s_1(v) - s_2(v)) (-v+ w) \ &= \sum_{v \in V} s_1(v) (-v+ w) - \sum_{v \in V} s_2(v) (-v+ w) \ &= div(s_1) - div(s_2) \end{aligned} $$

and is hence a group homomorphism.

div produces divisors of degree 0: deg(div(s)) = 0.

See that $div$ is balanced, in that for every $-v$ we have a $+w$. This makes the total degree zero.

Principal divisors: $Prin(G) \equiv div(M(G))$.

• Divisors of the form div(s) are called as Principal divisors. They are a subgroup of the degree 0 divisors.

• Moreover, if $D'$ is obtainable from $D$ by a series of lending and borrowing moves, then $D' - D \in Prin(G)$.

• This means that linear equivalence is a coset of the principal divisors: $[D] = D + Prin(G)$.

Picard, Jacobian Class group as quotients

• $Pic(G) = Div(G)/Prin(G)$.
• $Jac(G) = Div^0(G)/Prin(G)$.
• $Pic(G), Jac(G)$ are class groups because we get equivalence classes of divisors, equivalent upto principal divisors.

div is same as laplacian

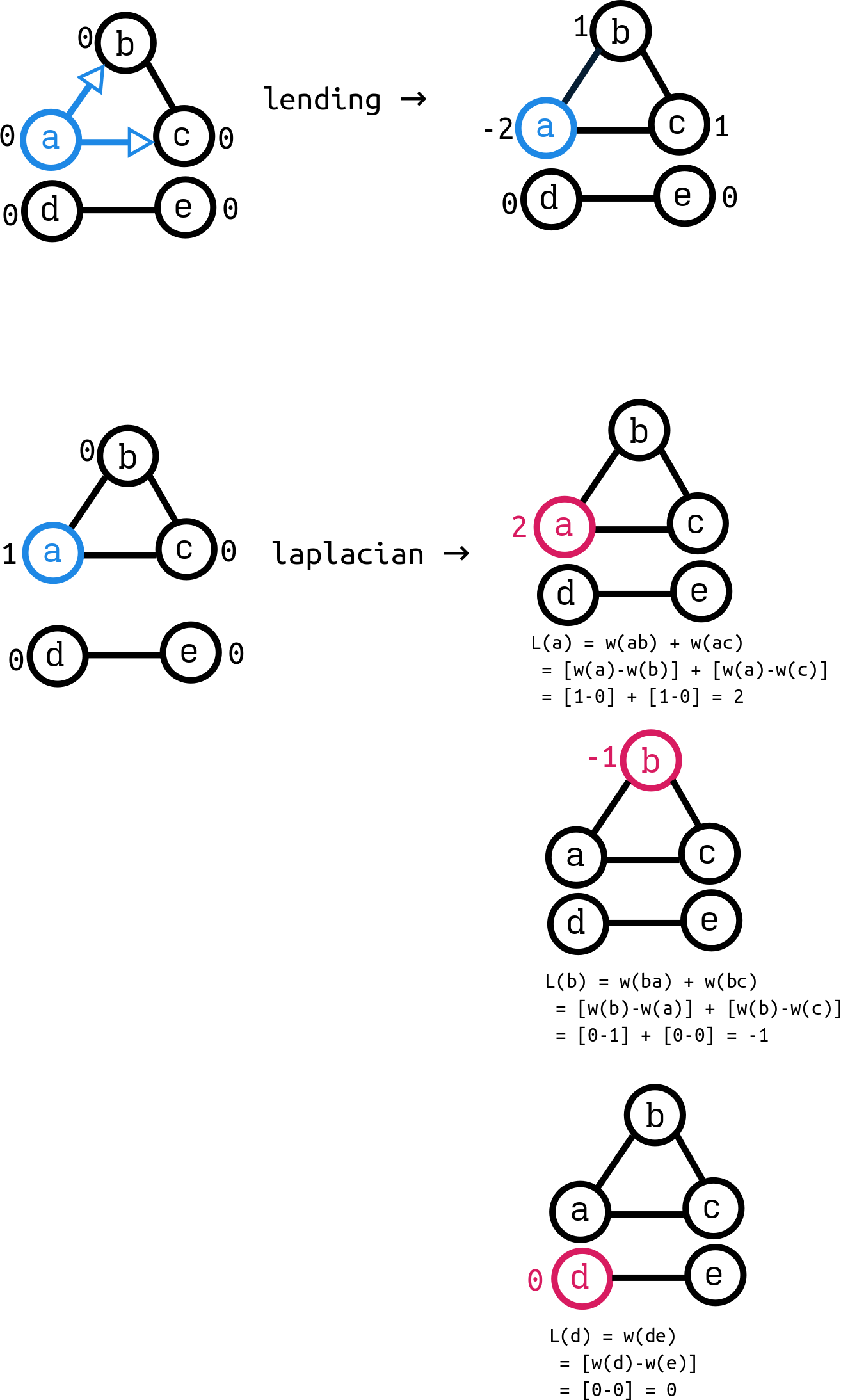
Picard group is cokernel of L

Recall that Pic(G) = Div(G)/Prin(G), where Prin(G) was the collection of divisors that could be realised from a firing script. That is,

$$ Prin(G) \equiv { div(s) : s \in V \rightarrow \mathbb Z } $$

M(G) -div→ Div(G) -quotient→ Pic(G) → 0
|          |
f          g
|          |
v          v
Z^n  -L→   Z^n   -quotient'→ cok(L) ~= Z^n/Im L → 0

• The quotient map quotient is surjective.
• The map quotient' is also surjective

Dollar game in terms of laplacian

given a divisor $D$, does there exist a vector $x \in \mathbb Z^V$ such that $D + Lx \geq 0$?

Clearly, this is some sort of linear inequality. So, we expect polytopes to show up! Since $x$ is an integer point, we want integer points in polytopes.

Kernel of laplacian in connected graph: all 1s vector

• first of all, see that lending by everyone in $V$ has no effect: everyone lends to all their neighbours, and all their neighbours lend to them, having zero net effect.

• Stated in terms of the firing script, this means that $s_1 + s_2 + \dots s_n$ is in the kernel of $div$: the firing script creates a zero divisor. If we choose a basis, this is the all 1s vector.

• In terms of the laplacian, this is stating that the all ones vector is in the kernel of the laplacian.

Kernel of laplacian in connected graph: constant functions (TODO)

Suppose we have a script $s: V \rightarrow \mathbb Z$ such that $div(s) = 0$.

**TODO **

This feels sheafy to me, in terms of "locally constant".

Reduced laplacian: Configurations on $G$

We build reduced laplacians to relate the jacobian (degree zero elements of divisor class group) and the laplacian.

Fix a vertex $q \in V$. Define $\tilde{V} \equiv V /{q}$. A configuration on $G$ with respect to $q$ is an element of the subgroup

$$ Config(G, q) \equiv \mathbb Z \tilde{V} \subseteq ZV = Div(G) $$

so we simply forget the value at $q$. Alternatively, we set the value of $q$ to zero and continue will our divisor definitions.

We can perform lending and borrowing on a configuration divisor, by simply not tracking data at $q$.

3: Winning

q-reduced configurations

We wish to solve the game by benelovence: have vertices lend to adjacent vertices. Here are the steps to convert such an intuition to a real algorithm:

1. Start with a divisor $D$ we want to find an effective divisor $E \geq 0$ that $D$ is linearly equivalent to (ie, there exists a series of moves to convert $D$ to $E$).
2. Pick some benelovent vertex $q \in V$. Call $q$ the source. Let $V' = V/q$ be the non source vertices.
3. Let $q$ lend so much money to the non-source-vertices, such that the non-source-vertices, sharing amongst themselves, are out of debt.
4. Now only $q$ is in debt from this giving. $q$ makes no lending or borrowing moves. The non-source-vertices must get $q$ out of debt. Find a $S \subseteq V'$ such that if everyone in $S$ lends, then no one in $S$ go into debt. Make the corresponding set-lending move. Repeat until no such $S$ remains. The resulting divisor is said to be $q$-reduced.

In the end, if $q$ is no longer in debt, we win. Otherwise, $D$ is unwinnable.

Superstable configuration

Let $c \in Config(G, q)$. It is called superstable if $c \geq 0$ and has no legal non-empty set firings. That is, for each non-empty $S \subseteq V/q$, we have some $v \in S$ such that firing $v$ would cause $v$ to go into debt; that is, $c(v) < outdeg_S(v)$.

Decomposition of divisor into superstable configuration

Every divisor can be written as $D = c + kq$ where $c \in Config(G, q) \geq 0$. In this form, $D$ is $q$-reduced iff $c$ is superstable! This follows from the definition of $q$-reduced: there is no subset $S$ which can be fired such that $S$ stays out of debt. Now, if $q \geq 0$, then we win, from what we know of $q$-reduced configurations.

4: Acylic orientations

Orientations

An orientation of a graph makes each edge directed. We think of edges now as tuples $e \equiv (u, v)$ as an edge from $u$ to $v$. We denote $e^- = u$ and $e^+ = v$ to be the source and sink vertices of the orientation.

Acylic orientations

An orientation is acyclic if there are no cycles. Every acylic orientation must have at least one sink and a source. It must have at least one source. Assume the acyclic orientation does not have any sources.

Acylic orientation has at least one source

Pick any vertex . If it is a source, done. If it is not a source, it has a parent. Go to parent that has NOT BEEN PICKED YET, repeat check. We will eventually:

• Find a source vertex (vertex with no parent)
• All parents of current vertex have been picked (ie, we find a cycle). Can't happen.

Thus all acyclic orientations have at least one source.

Indegree sequence of an acyclic orientation.

If $O$ is an orientation, define

$$ indeg_O(u) \equiv |{ e \in O : e^+ = u }| $$

That is, to each $u$, associate the number of edges whose end is at $u$.

WRONG: Acylic orientation determined by indegree sequence?

The book claims that acyclic orientation is determined by the indegree sequence. I don't believe this. Consider the graph $G$:

--a--
|   |
v   v
b   c

• This has indegrees $(a=0, b=1,c=1)$.

Now consider $H$:

a
|
v
b
|
v
c

• This has indegrees $(a=0, b=1, c=1)$ but the graphs are not equal!

Acylic orientation determined by indegree sequence

OK, the above is not what the book claims. The book claims that two orientations $O_G$, $O'_G$ of the same graph are equal if their indegree sequences are equal.

This is believeable, because if the orientations point differently, their indegrees will change.

• Proof strategy: induction on number of vertices + forcing sources to be the same + creating new sources by removing current sources.

• Theorem is immediate with only one vertex. Assume holds for $n$. Now we have a graph with $(n+1)$ vertices. Find source in acyclic orientation $O_G$. This has no incoming edges, so has indegree zero. This must be the same in $O'_G$ since $O_G$ and $O'_G$ have the same indegree sequence.

• Now remove the sources that are structurally equal. We get a graph of $H$ of (n-1) vertices, and we get $O_H$ and $O'_H$ by removing the sources from $O_G, O_G'$. Since $O_G = O_G'$ we must have that $O_H = O_H'$ since removing the same source from both graphs modifes the orientations the same way. Recurse into $O_H, O_H'$.

Divisor for an orientation

For an orientation $O$ we define a divisor $D(O)$ as:

$$ D(O) \equiv \sum_{v \in V}(indeg_O(v) - 1) v $$

5: Riemann roch

The rank function

In one sense, the “degree of winnability” of the dollar game is measured by the size of complete linear systems: $D$ is “more winnable” than $D'$ if $[D]{\geq 0} > [D']{\geq 0}$. Instead of measuring $[D]_{\geq 0}$, we choose to define another function, the rank, that measures "stability/robustness of winnability"

• Fist, $r(D) \equiv -1$ if $D$ is unwinnable: $r(D) \equiv 0$ iff $[D]_{\geq 0} = \emptyset$

• Next, $r(D) = 1$ if $D$ is barely winnable. That is, $D$ is winnable, but there is some vertex $v$ such that $D - v$ is unwinnable. That is, $r(D)$ is barely winnable if the ability to win at $D$ can be destroyed by a single vertex losing a dollar.

• In general, for $k \geq 0$, define that $r$ is at least $k$ winnable if the dollar game is winnable strating from all divisors obtained from $D$ by removing $k$ dollars. Formally, this becomes:

$$ r(D) \geq k \iff |D - E| \neq \emptyset \text{for all $E \geq 0$ ($E$ effective) of degree $k$} $$

This means that $r(D) = l$ if there is some divisor $E$ of degree $l+1$ such that $D - E$ is not winnable.

$r(D)$ is upper bounded by degree: $r(D) \leq deg(D)$

if $D$ is of degree 0, then rank is 0 iff $D$ is principal

$r(D) \leq r(D + v) \leq r(D) + 1$: adding a dollar can increase rank by at most 1

$r(D + D') \geq r(D) + r(D')$: rank is super-linear.

Lower bound on rank: $r(D) \geq deg(D) - g$

Won't prove this here, depends on other results (if $deg(D) \geq g$, then $D$ is winnable)

Canonical divisor

For any orientation $O$, define $O_{rev}$ to be the reversed orientation. Now define the canonical divisor $K$ to be $K \equiv D(O) + D(O_{rev})$. See that for every $v \in V$:

$$ \begin{aligned} K(V) = indeg_O(v) + outdeg_O(v) = deg_G(v) \end{aligned} $$

References

• This answer on mathoverflow that asks about how to understand divisors of elliptic curves
• Specialization of linear systems from groups to graphs
• riemann-roch and abel-jacobi theory on a finite graph
• Divisors and Sandpiles: An Introduction to Chip-Firing

Conversation with Olaf Klinke

do you have reading you'd recommend to gain your viewpoint of computation-as-topology-as-computation?

I am a topologist, a domain theorist to be more precise. I had the privilege to meet many founders of this relatively young field of mathematics. Domain theory is a denotational semantics (there are others) of lambda calculus. For reading, there is the old testament and the new testament, as I call it. The old testament is "A compendium of continuous lattices" ISBN 3-540-10111-X
ISBN 0-387-10111-X The new testament is "Continuous lattices and domains" ISBN 0-521-80338-1

Domain theory makes sense once one stops disregarding bottom |, or undefined. Think of domains as triangular objects, e.g. the type Bool

False   True
    \   /
     _|_

How does one compute a real number? Think of a horizontal real interval, and draw a triangle underneath:

---[---]---
\   \ /   /
 \   .   /
  \     /
   \   /
    _|_

Every point in the triangle represents a closed interval. At the top is a copy of the real numbers in the form of singleton intervals, the "total" elements. Every point underneath is a proper interval, representing everything reachable by "fanning out" upward from that point. This may be a model for e.g. interval arithmetic, where computing a more precise result means moving up in the triangular domain of intervals. Directed suprema (results of recursive computations) in this domain are nested intersections of intervals. Existence of these directed suprema is equivalent to the uniqueness and non-emptyness of the nested intersections, which again is guaranteed by the two topological properties "Hausfdorff" and "compactness" of the closed real interval.

A treasure trove of smart little Haskell programs is Martín Escardó's so-called Barbados notes, number 46 in https://www.cs.bham.ac.uk/~mhe/papers/index.html

Topological groups and languages

MonoidNull is a monoid that allow us to test for mempty. So it obeys the law:

class Monoid m => MonoidNull m where
    null :: Monoid m => m -> Bool
    -- null x == x == mempty

There are MonoidNulls that don't have an Eq instance. For example, consider Maybe (Int -> Int), where the monoid over (Int -> Int) adds them pointwise. Clearly, we can't tell when two functions are equal, so there's no way we can give an Eq instance to Maybe (Int -> Int). But we can definitely tell when it's Nothing! So we have a MonoidNull instance without an Eq instance.

Now the interesting thing is that if we have a group that has MonoidNull, then it automatically has Eq! Witness:

instance (Group g, MonoidNull g) => Eq g where
   x == y = null (x <> inv y)

See that this is a transport principle: we're able to transport the test of equality at the origin/mempty provided by null to any point in the group.

Olaf Klinke remarked:

A beautiful example of topological groups: Their topology is completely determined by the neighbourhoods of the identity element. If the identity element is isolated, the entire group is discrete.

I found this very interesting, because he's vieweing this from the "topology of computation" lens, where the existence of null means that the identity element is isolated. Now since it is a topological group (group operations are continuous since everything is computable!), the isolatedness of the identity transports to all points, giving us a discrete object where equality is decidable! Below is an illustration of how I imagine the situation.

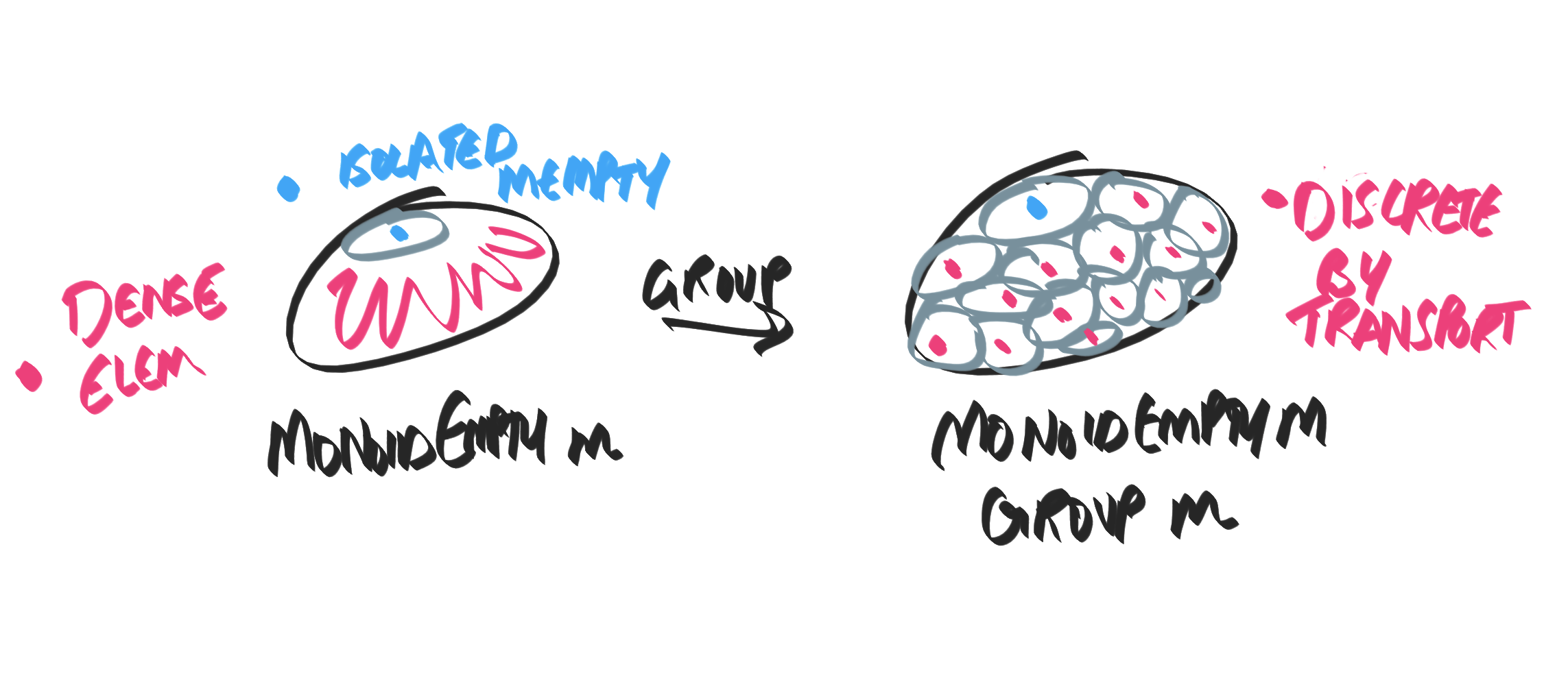
References

• Post on haskell-cafe by Olaf Klinke

Killing fields (WIP)

References

• Killing vector field

The mnemonica stack (WIP)

4  c♣
2  h♡ 
7  d♢
3  c♣
4  h♡
6  d♢
A  s♠
5  h♡
9  s♠
2  s♠
Q  h♡
3  d♢
Q  c♣
8  h♡
6  s♠
5  s♠
9  h♡
K  c♣
2  d♢
J  h♡
3  s♠
8  s♠
6  h♡
10 c♣
5  d♢
K  c♣
2  s♠
3  h♡
8  d♢
5  c♣
K  s♠
J  d♢
8  c♣
10 s♠
K  h♡
J  c♣
7  s♠
10 h♡
A  d♢
4  s♠
7  h♡
4  d♢
A  c♣
9  c♣
J  s♠
Q  d♢
7  c♣
Q  s♠
10 d♢
6  c♣
A  h♡
9  d♢

• YouTubevideo with chant

Conversation with Alok about how I read

Alok Debnath, a friend of mine claims he understood "how I read" based on reading infinite jest and setting me experiments that allowed him to observe how I read.

In his words:

Alok: I have seen you spasm on your cursor trying to read text (WIP: get a longer quote form alok about what this means)

He said that he never understood what the fuck I was doing until he read Infinite Jest by David Foster Wallace (a phenomenal book, I loved it and recommended it to him, which were enough recommendations to get him to read it, it seems).

Infinite jest

Alok: It took me reading that book twice to understand how you process text. Let's deep dive. You don't read sentences, from what I remember. You have a different model of chunking text. For what it's worth, I tried to remember what you spasm between when skimming vs when reading. There does not seem to be much difference between those modes for you, which was interesting. So I tried to note why you would sometimes go BACK rather than read sentence to sentence. I figured it was one of three things:

The three things are:

1. You went from verb to verb or action to action, or event to event, and then determined the significance of that event. You would move backwards only if the verb was significant enough to warrant its arguments being understood
2. You went from topic to topic, and would only go BACK if you think you missed a timestep in the movement between topics.
3. You read from line to line, regardless of the sentence, phrase, clause or syntactic structure, and would only go back if an item caught your attention.

According to him, I do a combination of 1 and 2, in contrast to others who might do (3).

Why this works for me

you are uniquely adaptive to reading style, based on very little information. This is a good thing when there is a unique, singular style to the entire article, it is easy to templatize and then retrofit into how you want to get that information.

His take on my take on why SEP is trash

I ran a series of experiments to figure this out. I'd ask you to read a paper, a textbook chapter or something in front of me, and after you'd read a paragraph, ask you to explain it. Some times you were already reading something (mostly philosophy related) and that's ambush. Lastly, I used SEP as bait .SEP has not been written for people like you. And I was thoroughly surprised at your vehement disapproval to some of the articles (for their content ofc), but your veiled stylistic inputs as well.

you mentioned that the text of the SEP article on Derrida was malformed, which is a stylistic input, rather than a content issue.

He figured out that the SEP entry has been written in two merged styles - one is a list of topics that Derrida talks about The other is a list of events which weave together how those topics became tenets of his philosophy. The style of writing generally based on the modern notion of "set-inductive" introductions to topics Which doesn't work well with you. Because I then noticed how you read code And I figured that you need to have a trace of the topics talked about in case they appear again in the code, and you parse blocks, retrieve need, GC, and move on to the next block. So order of arguments and the state of these topics remains in your mind, along with significant events. debnatak: You read text in a similar way, which is why set inductive writing is the worst way to write for you.

Inductive writing

Apparently, this is a common philosophy of teaching where one is exposed to a topic by "forewarning" them of all the subtopics, then a narrative is weaved exploring the relationship between each subtopic, explaining them as they come. It's the style in which school textbooks are written. So it is neither ordered by event, nor ordered by topic. It's the job of the teacher to guide the student across the text.

Now, the Derrida SEP article is written in a very similar manner, albeit a bit more well formed in narrative The text is not written in a manner where you can parse things by topic(i.e. first deconstructionism, then universality, then sovereignty) or by event (publishing book1 , then 2, then 3 or whatever). Therefore, this writing style is completely adverserial to your reading style!

Why I enjoy DFW and infinite jest

Infinite Jest, and DFW in general, clearly does not write like this. It is the antithesis, almost Your insane experience in garbage collection works when there are a large number of interconnected stories, people and threads being referenced in the same sentence.Given that you chunk differently, parse differently, and organise mental notes on what you have read differently than I do, it is not surprising that you understood DFW fairly well. DFWs writing style almost wholeheartedly abandons prescriptivist notions of punctuation and syntactic structure beyond the meager subject verb agreement, Which I think is also abandoned in some monologues. That would not be a large issue for someone who does not use punctuation as a mechanism of parsing sentence information, or even as an anchor of "begin here" and "end here".

Inference from me reading code?

According to him, this is similar to how I read code:

I saw you read word2vec.c in front of me And I was mindfucked at how you abstract information on the go Like you read bracket to bracket (I think), and keep track of "important" variables, especially function arguments and return values, and just summarize the rest debnatak: Not every operation needs to be understood, of course. But it is noted regardless. Functions are skipped over if not called, variables are ignored if not used. debnatak: You were never confused about the program flow debnatak: Idk, it seemed clean for code, and math ofc because representations

eye tracking data

KMP (Knuth, Morris, Pratt) (WIP)

References

• KMP in haskell
• String algorithms: Borders, KMP: video
• Geometric point pattern matching

Reading C declarations

The real rule turns out to be simple (although non-obvious): "Declaration matches usage." So, for example, if you want a pointer to a function returning a pointer to an array of 3 integers, you'd want

(*(*f)())[3 - 1]

to evaluate to an int, so the declaration would be

int (*(*f)())[3];

Make mnemonics

• [email protected]: target, since it looks like a target.

• $<: the 1st prereq, since < points to the left.

• $^: all prereqs, since ^ looks like an "upward grouping flower bracket".

• $?: prereqs that are newer than the target, since ? is stuff you don't know / haven't looked at.

• $*: target with suffix deleted, since we generally grep for *.c|h|, we want the * part of [email protected]. Alternatively, * is also like a target, but only the bull's eye with the extra stuff like the suffix stripped out.

• The POSIX makefile page which is WAY more readable

• notes for new make users

Vandermonde and FFT

FFT lets you do the following:

You are given two sequences: a0,...,an and b0,...,bm Compute sequence c0,…,c[n+m] such that $$c[i]=a[0]b[i]+a[1]b[i−1]+ \dots +a[i−1]b[1]+a[i]b[0]$$

This is exactly what I needed here, where $a[i]= \binom{n}{i}$ and $b[i]= \binom{m}{i}$. If I thought for a little longer I would realize that $c[i]=\binom{n+m}{i}$ instead of computing it using FFT.

References

• [Codeforces contest comment by Swistakk)[https://codeforces.com/blog/entry/85348?#comment-730898]

Thoughts on blitz chess: 950 ELO

I plan on summarizing my current thoughts on chess at different stages of ELO on Lichess. This should be fun to look back on. Currently, I found that the thing that helps me the most when it comes to winning is this simple kernel:

Attack.

With the somewhat useful addendum:

With a plan.

That's it. That's literally all I need to do. I generally try to focus on the weak f pawn, get my Queen out early (people at my ELO rating don't really know how to punish an early roaming queen. I don't know either!), at just attack.

If there's an attack on your pieces, don't defend, counter-attack. Of course, there are situations where one must defend. Only defend then.

Getting into this frame of reference stopped me from languishing at ~800 ELO. I used to

• get anxious about the game and the prospect of conflict.
• get anxious about the clock.
• get anxious about leaving pieces hanging.

It seems that "getting over" these anxieties took ~20 games, after which I could focus on the mechanics. This is a good reference point, since I have the same problem with competitive programming --- the exact same anxieties, in fact.

Periodic tables and make illegal states unrepresentable

The periodic table of elements succeeded because the "gaps" in the table consisted of only legal atoms --- thus, by making illegal states unrepresentable, a table of the current state of knowledge becomes valuable because all the gaps are legal states. The exact same thing happened with juggling and juggling notattion.

Big list of questions on the structure of graphs

I've been trying to get more of a feeling for graphs lately, so I'm collecting sources of "structural" questions of graphs and answers for these questions.

Q. Is it possible in an unweighted graph, there is exactly one unique shortest path tree for a node u but more than one such shortest path tree for some other node v ?

Q. Can I orient the edges of a bridge-less undirected bipartite graph with even no. of nodes such that all the nodes are in a cycle ?

Combinations notation in bijective combinatorics

They explicitly write $nCr$ as $[n]C[r, n-r]$. This makes it better for "future uses", where it explicitly allows us to think of $[n]C[x, y]$ as breaking $n$ into $x$ things we choose and $y$ things we don't choose.

This makes the recurrence:

$$ [n]C[r] = [n-1]C[r-1] + [n-1]C[r] $$

look as:

$$ [n]C[r,n-r] = [n-1]C[r-1,n-r] + [n-1]C[r, n-r-1] $$

That is, we are reducing on either the first component ($r-1$) or on the second component ($n-r-1$), in the smaller set ($n-1$).

Arguments for little endian

Say we wish to store <MSB> 100 200 300 400 <LSB>. In little endian, this would be stored as:

ix:   0   1   2   3
val:  400 300 200 100

An interesting theory for why this is good is if we want to treat this 4-bit data as 1-bit data, we want the subarray [400]. It's easier to directly acess in little endian as just data[0], instead of in big endian where it would be data[3]. So, storing stuff backwards makes it easier to chop off the LSBs data, since that's the suffix.

Expectiles

Mean is a minimiser of $L_2$ norm: it minimizes the loss of penalizing your 'prediction' of (many instances of) a random quantity. You can assume that the instances will be revealed after you have made the prediction.

If your prediction is over/larger by $e$ you will be penalized by $e^2$. If your prediction is lower by $e$ then also the penalty is $e^2$. This makes mean symmetric. It punishes overestimates the same way as underestimates.

Now, if you were to be punished by absolute value $|e|$ as opposed to $e^2$ then median would be your best prediction.

Lets denote the error by $e_+$ if the error is an over-estimate and $e_-$ if its under. Both $e++$ and $e_-$ are non-negative. Now if the penalties were to be $e_+ + a e+-$ that would have led to the different quantiles depending on the values of $a > 0$. Note $a \neq 1$ introduces the asymmetry.

If you were to do introduce a similar asymmetric treatment of $e_+^2$ and $e_-^2$ that would have given rise to expectiles.

Depth first search through linear algebra (WIP)

References

• Talk Video
• Link to paper

2-SAT

First break into SCC's. Each SCC represents equivalence: since there is a path from every variable to every other variable, they must take on the exact same value. Hence if $x$ and $\lnot x$ are in the same SCC, we don't have a solution, because this means that $\texttt{true} = \texttt{false}$ or $\texttt{false} = \texttt{true}$.

Let's say we find SCC's where this does not happen. Now, zoom out and think of the condensation DAG. We want to assign true/false to each node in the SCC DAG. How should we assign true/false? Say that $x$ and $\lnot x$ are in two different components. So this means that we have the possible orderings

• $x \implies \lnot x$: $\texttt{true} \implies \texttt{false}$ (Inconsistent!)
• $x \implies \lnot x$: $\texttt{false} \implies \texttt{true}$ (Consistent, principle of explosion)

Hence, if $x$ implies $\lnot x$, we should set $x$ to $\texttt{false}$. The other assignment is inconsistent.

Longest increasing subsequence, step by step (WIP)

• The science of Programming by Gries

On reading how to rule (WIP)

The prince

Arthashastra

The book of lord shang

Strongly Connected Components via Kosaraju's algorithm

We know that a directed graph can be written as two-levels, a top-level dag, with each node in the DAG being a condensation of the original graph. So we wish to discover the DAG, and then each condensation. We wish to view Kosaraju's algorithm as a "stronger topological sort" that works for general graphs, and not just DAGs.

Step 1: Discover the tree/DAG

Run a bog standard DFS on the graph and record entry and exit times, because that tell us everything we need to know about the DFS. Let's decide what to keep and throw away next.

Step 2: Think

If we had a DAG, then we would be done; We sort the nodes according to descending order of exit times, and we get the topological order of the DAG. However, this is incorrect for our purposes, as this only gives us the components if we don't have cycles.

Step 3: Mix in cycle detection/single SSC

Pick the first node according the topological sort heurstic --- the node that's earliest according to exit time. We now need to discover cycles. Recall that we built the DAG according to DFS order, so if we run a DFS again, we'll get the entire subtree in the DAG! Rather, we want the "anti DFS": whatever can reach the 'root' of the 'DAG'. To find this, we reverse the DAG and find the component reachable from here.

SCC's as adjunction

I learnt this from Benjamin Pierce's "Category theory for computer scientists":

The strong components of a graph themselves form an acyclic graph that is a quotient of the original graph-that is, each node corresponds to an equivalence class of strongly connected nodes in the original. The mapping taking a graph to the acyclic graph of its strongly connected components may be expressed as a left adjoint to the inclusion functor from AcyclicGraph to Graph

References

• CS Cornell lecture notes

Articulation points

I find DFS fascinating, and honestly insane for how much structral information of the graph it manages to retain.

A vertex $v$ is an articulation point of a graph $G$ if the removal of $v$ disconnects the induced subgraph.

Tactic 1 - Inductively

We first solve the super easy case with the root, and then try to see if we can treat other cases like the root node case, then we're good. Here, we are given an graph $G$, and we are thinking about a DFS tree $T_G$ of the graph $G$.

Thinking about the root

When is the root an articulation point? If the root has multiple children, then it is an articulation point; If we remove the root, then it disconnects the children. This is because we have an undirected graph, where we only have back edges, and no cross edges. A back edge can only go from a node to its ancestor. If we remove the root, the back edges cannot save us, for there is no ancestor higher than the root to act as an alternate path

Non root vertex

When is a non root vertex $v$ an articulation point? When there is some child $w$ of $v$ such that the subtree of $w$ cannot escape the subtree of $v$. That is, all back edges from $w$ do not go above $v$. If we were to now remove $v$, then $w$ would be disconnected from the rest of the graph.

Alternate phrasing: When all cycles in the subtree of $w$ are within the subtree of $v$. This means that the backedges cannot go above $v$. If $w$ could build a cycle that goes above $v$, then $v$ would not be an articulation point, because it'll be involved in some cycle $v \mapsto w \mapsto \mapsto p \mapsto v$, which gives us an alternative path to reach $w$ even if $v$ is removed.

One way to imagine this maybe to imagine $v$ as the new root, and the other stuff that's above $v$ to be to the left of $w$. That way, if we could go to $w$, we get a cross edge from the "new root"(v) and the "other section" (the part that's connected by a cross edge). If we prevent the existence of these "fake cross edges", we're golden, and $v$ is then an articulation point.

Tactic 2 - Structurally / Characterization

Next we follow a "mathematical" development, where we build theorems to characterize k-connectedness and use this to guide our algorithm design

Menger's theorem

Let $G$ be a connected undirected graph. Let $u, v$ be two non-adjacent vertices. The minimum number of vertices whose removal from $G$ disconnects $u$ and $v$ is equal to the maximal number of vertex disjoint paths from $v$ to $u$.

Whitney's theorem (corollary)

An undirected graph is $k$ connected iff $k$ vertices must be removed to disconnect the graph.

Biconnected components

Menger's theorem tells us that a graph is not biconnected iff we can find a vertex whose removal disconnected the graph. Such a vertex is an articulation vertex.

A biconnected component is a maximal subset of edges, such that the induced subgraph is biconnected. Vertices can belong to many components; Indeeed, articulation vertices are those that belong to more than one component.

Lemma: Characterization of biconnected components

Two edges belong to the same biconnected component iff there is a cycle containing both of them. [This lemma is silent about biconnected components of single edges]

We show that a cycle is always contained in a single binconnected component. If a cycle contains edges from more than one biconnected component, then we can "fuse" the biconnected components together into a single, larger, biconnected component.

Lemma: Each edge belongs to exactly one biconnected component

Tactic 3 - 'Intuitively'

We look at pictures and try to figure out how to do this.

DFS for articulation vertices - undirected:

• The connectivity of a graph is the smallest number of vertices that need to be deleted to disconnect the graph.
• If the graph has an articulation vertex, the connectivity is 1. More robust graphs that don't have a single point of failure/articulation vertex are said to be binconnected.
• To test for an articulation vertex by brute force, delete each vertex, and check if the graph has disconnected into components. this is $O(V(V+E))$ time.

Joke: an articulate vertex is one that speaks very well, and is thus important to the functioning of the graph. If it is killed, it will disconnect society, as there is no one to fulfil its ability to cross barriers with its eloquent speech.

Articulation vertices on the DFS tree - undirected

• If we think of only the DFS tree for a moment of an undirected graph and ignore all other edges, then all interneal non-leaf vertices become articulation vertices, because they disconnect the graph into two parts: the part below them (for concreteness, think of a child leaf), and the root component.

• Blowing up a leaf has no effect, since it does not connect two components, a leaf only connects itself to the main tree.

• The root of the tree is special; If it has only one child, then it acts like a leaf, since the root connects itself to the only component. On the other hand, if there are multiple components, then the root acts like an internal node, holding these different components together, making the root an articulation vertex.

Articulation vertices on the DFS graph - undireced

• DFS of a general undirected graph also contains back edges. These act as security cables that link a vertex back to its ancestor. The security cable from x to y ensures that none of the nodes on the path [x..y] can be articulation vertices.

• So, to find articulation vertices, we need to see how far back the security cables go.

int anc[V]; int dfs_outdeg[V];
void processs_vertex_early(int v) { anc[v] = v; }
void process_edge(int x, int y) {
  if (dfsedge[x][y].type == TREE) { dfs_outdeg[x]++; }
  // y <-*
  //     |
  //     BACK
  //     |
  // x --*
  if (dfsedge[x][y].type == BACK && (parent[y] != x)) { 
     if(entry_time[y] < entry_time[anc[x]]) {
       anc[x] = y;
     }
  }
}

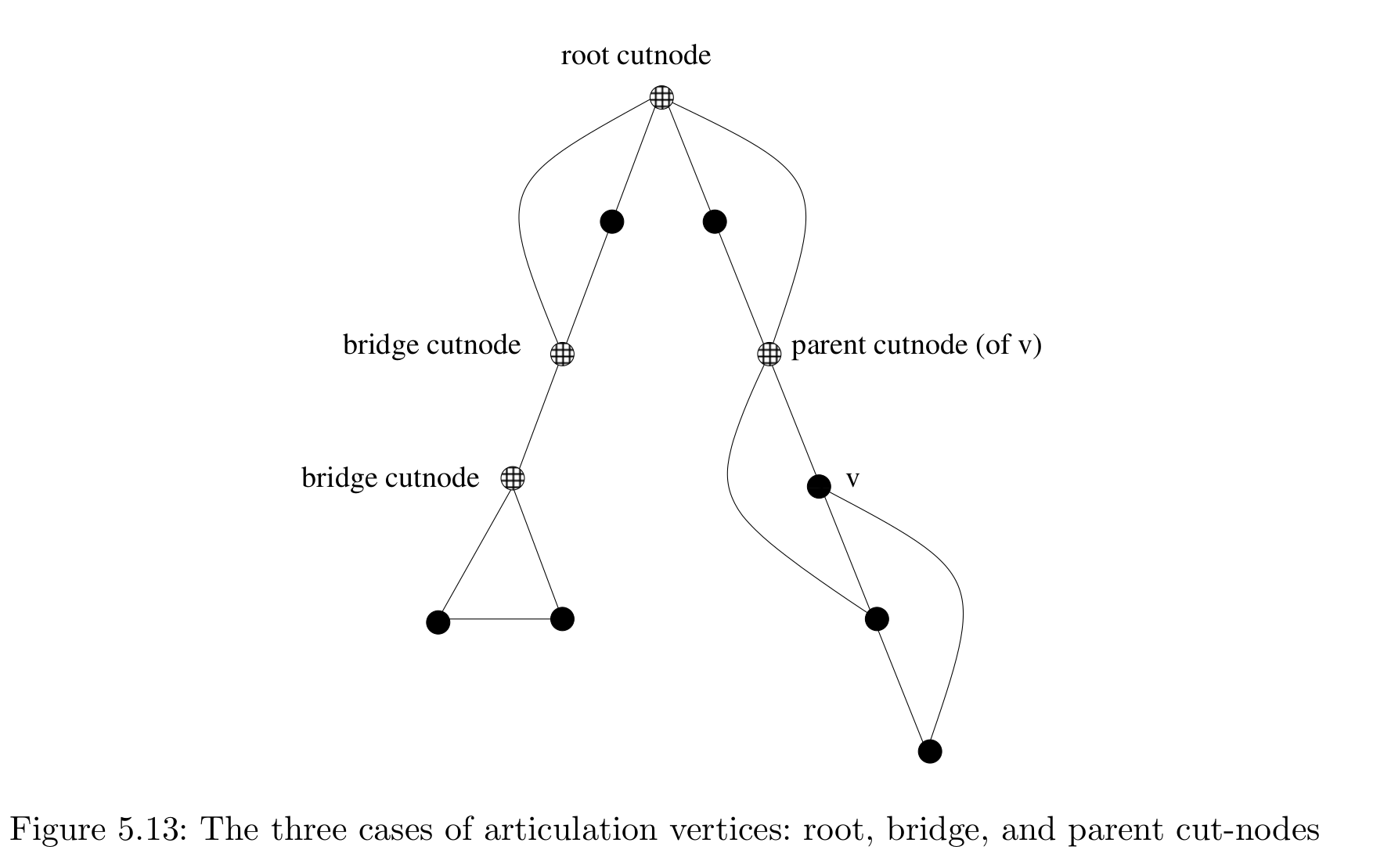
In a DFS tree, a vertex v (other than the root) is an articulation vertex iff v is not a leaf and some subtree of v has no back edge incident until a proper ancestor of v.

References

• Udi Manber: Introduction to algorithms: A creative approach.
• Steven Skeina: The algorithm design manual.
• Codeforces: problems to solve
• A2OJ articulation point problems
• INOI advanced graph algorithms

Disjoint set union

intuition for correctness of rank:

Assume that we had to re-point pointers of all our children to the new root when we decide to make another node the root. That is, we would have:

void mkroot(int newroot, int prevroot) {
   for (int child : children[prevroot] {
        parent[child] = newroot;
   }
   parent[prevroot] = newroot];
   children[prevroot] = {}; // this has no children anymore
}

• In this setting, we ought to make the smaller subtree the prevroot and the larger subtree the newroot: It is better to loop over fewer children.

• When we perform the rank based union, we are using the same heuristic, even though we don't actually loop over all our children.

Making GDB usable

• Use GEF

Bouncing light clock is an hourglass

I've always disliked the "clocks" that are used in special relativity, because a clock attempts to measure something absolute, rather than something relative. So, we should rather use hour glasses. In an hour glass, we can only measure intervals of time.

Now, when we have such an hourglass, we should fill the hourglass with photons, because their speed of falling is invariant for all reference frames. So, what we need is the ability to create an hourglass worth of photons which we keep dripping down, once the photon at the funnel has reached the bottom.

This is exactly what the two mirror photon clock does --- it bounces a photon between two mirrors. We can look at this as us "flipping" the hourglass once the photon reaches the bottom of the hourglass.

Euler tours

Tucker's proof: undirected graph with all even degree has an euler tour

I find this proof much more intuitive because it's extremely clear where the even condition is used.

1. For each vertex $v$, arbitrarily pair edges incident at $v$ to get chains u --- v --- w.
2. Connect chains to get cycles.
3. Find a spanning tree of cycles to get an euler tour, where we have an edge between two cycles if they share a common vertex.

It's super clear why we need all vertices to be even degree; You can't pair up vertices otherwise!

References

• Video on euler tour
• Notes from Emory course on graph theory
• CSTheory.stackexchange question on euler tours

Representation theory of the symmetric group (WIP)

• Video lectures: Representation theory, a combinatorial viewpoint

Maximum matchings in bipartite graphs

It turns out that the best way to do this is to simply implement Dinic's with scaling. That seems to meet the desired Hopcroft-Karp complexity. I was quite disappointed to learn this, since I was hoping that Hopcroft-Karp would have new ideas.

References

• Bipartite Graphs/Matching (Intro)-Tutorial 12 D1 Edexcel
• Maximum Matching Algorithm - Tutorial 13 D1 Edexcel A-Level
• Slides on matroid intersection

p-adics, 2's complement, intuition for bit fiddling

Consider the equation $x & (-x)$ which enables us to find the largest power of 2 that divides $x$. One can prove this relatively easily from the definitions:

$$ \begin{aligned} &a = \langle x 1 0^r \rangle \ &-a = \lnot a + 1 = x01^r + 1 = \overline{x}10^r \ &a & (-a) = a & (\lnot a + 1) = (x 10^r) & (\overline{x}10^r) = 0^{|\alpha|}10^r = 2^r \end{aligned} $$

That is, if we state that $a = \langle x 1 0^r \rangle$ for some arbitrary $r$, we then find that $a & (-a) = 2^r = \langle 1 0^r \rangle$, which is precisely what we need to subtract from $a$ to remove the rightmost/trailing $1$. However, I don't find this insightful. So I'm going to spend some time dwelling on $2$-adics, to find a more intuitive way to think about this.

2-adics and negative numbers

In the 2-adic system, we have that:

$$ \begin{aligned} &-1 = \dots 1 1 1 1 \ &-2 = -1 + -1 = \dots 1 1 1 1 + \dots 1 1 1 1 = \dots 1 1 1 0 \ &-4 = -2 + -2 = \dots 1 1 1 0 + \dots 1 1 1 0 = \dots 1 1 0 0 \ &-8 = -2 + -2 = \dots 1 1 0 0 + \dots 1 1 0 0 = \dots 1 0 0 0 \ \end{aligned} $$

Of course, these agree with the 2's complement representation, because the 2's complement representation simply truncates the 2-adic representation. At any rate, the point of interest is that if we now want to know how to write $-3$, we start with the "lower" number $-4$ and then add $1$ to it, giving us:

$$ -3 = -4 + 1 = \dots 1 1 0 0 + \dots 0 0 0 1 = \dots 1 1 0 1 $$

Which once again agrees with the 2's complement definition.

$x & (-x)$ for powers of 2:

If we now think strictly about powers of 2, we know that, for example, $8 = \langle \dots 0 0 1 0 0 \rangle$ while $-8 = \langle \dots 1 1 1 0 0 \rangle$. Hence, $x & (-x) = \langle 0 0 1 0 0 \rangle$. This will hold for any power of 2, so our claim that $x & (-x)$ gives us the location of the LSB will work for any power of 2.

Alternative explanation for 2's complement

Start with the fact that we choose a single representation for zero:

0 ~= b0000000

Now, when we subtract 1, ask "are we in signed world or unsigned world"? If in signed world, we want the answer to be -1. If in unsigned world we want the answer to be 255.

0 - 1 
= b0000000 - b00000001
= b11111111 
=unsigned= 255

If we wanted to interpret the answer as signed, then we are free to do so. This automatically tell us that

0 - 1
=unsigned= b11111111
=signed= -1

So, the advantage is that our operations don't care about whether the number is signed/unsigned.

Diameter of a tree

Key property of the diameter

• Let $p$ be a path of maximum diameter, which starts at $p$ and ends at $q$. Consider a tree where the diameter is shown in golden:

• We claim that a node at distance $d$ from the left can have a subtree of height at most $d$:

• Suppose this were not the case. Then, we can build a longer diameter (in pink) that is longer than the "supposed diameter" (in gold):

Algorithm to find the diameter:

First perform DFS to find a vertex "on the edge", say $v$. Then perform DFS again starting from this vertex $v$. The farthest vertex from $v$, say $w$ gives us the diameter (the distance from $v$ to $w$)

Proof by intuition/picture:

• first imagine the tree lying flat on the table.

• Hold the tree up at node $c$. It's going to fall by gravity and arrange as shown below. This is the same as performing a DFS.

• Pick one of the lowest nodes (we pick $g$). Now hold the entire tree from this lowest node, and once again allow gravity to act.

• This will give us new lowest nodes such as $b$. This node $b$ is going to be diameter, "because" it's the distance from a lowest node to another lowest node.

Catalan numbers as popular candidate votes (WIP)

• Usually, folks define catalan numbers as paths that go up or right from $(1, 1)$ to $(n, n)$ in a way that never goes below the line $y = x$.

• The catalan numbers can be thought to model two candidates $A$ and $B$ such that during voting, the votes for $A$ never dip below the votes for $B$.

I quite like the latter interpretation, because we really are counting two different things (votes for $A$ and $B$) and then expressing a relationship between them. It also allows us to directly prove that catalan(n) is equal to $1/(n+1) \binom{2n}{n}$ by reasoning about seqences of votes, called as ballot sequences

Ballot sequences

References

• Richard Stanley's slides

The chromatic polynomial (WIP)

I've been on a combinatorics binge lately, so I'm collecting cool facts about the chromatic polynomial. We first define the chromatic function of a graph, which is a generating function:

$$ fG \equiv \texttt{number of ways to color $G$ with $x$ colors} \cdot x^n $$

If we have a single vertex $K_1$, then $fK_1 = n x^n$, since we can color the single vertex with the $n$ colors we have.

Composition of chromatic funcions of smaller graphs

The chromatic function is a polynomial

Structure theory of finite endo-functions

We study functions $f: V \rightarrow V$ and their properties by thinking of them as a graph with vertex set $V$ and directed edges $(v, f(v))$. This gives us insight into permutations, rooted trees, and a bunch of counting principles. Such a structure is called as functional digraph

Principle 1: Structure theory

every functional digraph uniquely decomposes into disjont rooted trees which feed into one or more disjoint cycles. We think of nodes as pointing from the leaves towards the root. The root of the tree lies in a cycle.

Existence of tree implies not bijection

If we have a tree, we can keep walking backwards using edges from the root towards the leaves. Now this leaf does not have an incoming edge. This means that this leaf is not in the image of $f$. Hence $f$ cannot be surjective.

Rooted Trees: a single cycle

in a rooted tree, only the root node $r$ is such that $f(r) = r$. All other nodes point to other nodes without cycles.

Permutations: no rooted tree, only cycle

In a permutation, all we have are cycles. There are no trees that hang from the cycles.

Counting number of rooted trees: $n^{n-2}$: (WIP)

Say we have a function $f: V \rightarrow V$ where $|V| = n$ and $f(1) = 1$, $f(n) = n$.

References

• USACO: functional graphs

Number of paths in a DAG

Given the adjacency matrix $A$ of a DAG, this must be nilpotent. This is because $A^k[i][j]$ will tell us the number of paths from $i$ to $j$ with $k$ edges in the path. In a DAG, since there are no cycles, there is an upper bound on the number of edges a path can have: the longest path is $|V| - 1$, when the DAG is a straight line. Thus, we must have that $A^|V| = 0$.

• Let $A^n = 0$.
• Now, we know that $(I - A)^{-1} = I + A + A^2 + \dots$ which will terminate as a finite sum, with $(I - A)^{-1} = I + A + A^2 + \dots + A^{n-1}$.
• But note that $(I + A + A^2 + \dots A^{n-1})[i][j]$ will count number of paths from $i$ to $j$ with $0$ edges, $1$ edge, $2$ edges, etc. so we will get the total number of paths from $i$ to $j$!.

Set partitions

Let $X$ be a set. A breakup of $X$ into pairwise disjoint sets $A[i]$ such that $\cup_i A[i] = X$ is called a partition $P$ of the set $X$.

Stirling numbers of the second kind: $S(n, k)$

These count the number of ways to break an $n$ element set into $k$ partitions/equivalence classes.

The recurrence is:

$$ S(n, k) \equiv S(n-1, k-1) + kS(n-1, k) $$

• For the $n$th element, I either build a new equivalence class ${ n }$ and then make $k-1$ equivalence classes from ${1\dots (n-1)}$.
• Alternatively, I have $k$ equivalence classes from ${1 \dots (n-1)}$, say $P[1], P[2], \dots, P[k]$ I decide into which $P[i]$ the $n$ should go, which gives me $k$ choices.
• Initial conditions: $S(0, 0) = 1$, $S(0, k \neq 0) = S(n \neq 0, 0) = 0$.

Stirling numbers and surjections

Interesting interpretation: The number of ways to surject an $n$ element set into a $k$ element set, since a surjection breaks a set up into a known number of fibers (in this case, $k$ fibers).

This is not entirely true, because we only get $k$ equivalence classes of the set ${1, \dots, n}$. We need to decide where to map each equivalence class. So the correct count of ${ [n] \xrightarrow{onto} [k] }$ is $k!S(n, k)$: there are $k!$ ways to map equivalence classes of $n$ to elements of $k$

Rook theory(!)

Turns out we can provide a crazy relationship betweeen ferrers diagrams, and rooks (as in the chess piece) and stirling numbers of the second kind.

We define $\Delta(n)$ to be the board consisting of the integer partition $[n-1, n-2, \dots, 1]$. For example, we think of $\Delta(4)$ as:

Delta(4):
+--+
|  |
+--+--+
|  |  |
+--+--+--+
|  |  |  | 
+--+--+--+--+

Hopefully, this looks like a staircase with 4 stairs starting from the ground. We have filled in squares of $[3, 2, 1]$ blocks stacked above one another.

We define $r(n, k)$ to be the number of legal rook placements on a board $\Delta(n)$ with $k$ free rows. That is, we have $(n-k)$ rooks to place on the board $\Delta(n)$, with one on each row, such that no rook attacks another rook.

• Boundary condition: $r(0, 0) = 0$ 0 free rows on a $\Delta(0)$ board counts as one configuration.

• Recurrence: $r(n, k) \equiv r(n-1, k-1) + k r(n-1, k)$

• $r(n-1, k-1)$ term: We don't place a rook on the bottom row. This means we have used up a free row, and need to place rooks with $(k-1)$ free rows on an $(n-1)$ board:

+--+
|  |
+--+--+
|  |  |  r(n-1, k-1)
+--+--+--+

+--+--+--+
|  |  |  |  BLANK
+--+--+--+--+

• $k r(n-1, k)$: We fill out $\Delta(n-1)$ with rooks such that we have $k$ free rows. Then, we add the final row. Note that since we have rooks, $k$ free rows is equivalent to $k$ free columns! Now, we can't leave the final row free, since we have already exhausted our $k$ free rows in the recursion. We have $k$ free columns for the rook in the final row to inhabit. So we get $k r(n-1, k)$.

Bijection between rooks and Stirling numbers of the second kind

Finally, note that $S(n, k) = r(n-k, k)$, as $S(n, k) = S(n-1, k-1) + k S(n-1, k)$ which is equivalent to asking:

$$ \begin{aligned} &S(n, k) = S(n-1, k-1) + k S(n-1, k) \ &r(n-k, k) =? r(n-1 - (k-1), k-1) + k r(n-1 - k, k) \ &r(n-k, k) =? r(n-k, k-1) + k r(n-k-1, k) \ &\text{set $m = n-k$: } \ &r(m, k) = r(m, k-1) + k r(m, k) \ \end{aligned} $$

Directly reading off the bijection between set partitions and rook placements

I found this very cool. The idea is to treat each rook as a "bouncer" that bounces light rays. All elements hit by a light ray belong to an equivalence class.

Wrooks and signless stirling numbers

Similar to the rooks, we define a wrook (a weak rook) as one that only attacks on its row. Here $w(n, k)$ denotes a placement of wrooks on $\Delta(n)$ with $k$ free rows.

$$ \begin{aligned} &w(n, k) \equiv \ &~ w(n-1, k-1)~ \text{Leave bottom row free: uses up a free row} + \ &n w(n-1, k) \text{Place a wrook on bottom row: $n$ possible positions} \end{aligned} $$

The corresponding "counting" object is called as the signless stirling numbers:

TODO

Integer partitions: Recurrence

An integer partition of an integer $n$ is a sequence of numbers $p[1], p[2], \dots p[n]$ which is weakly decreasing: so we have $p[1] \geq p[2] \dots \geq p[n]$. For example, these are the integer partitions of $5$:

• [5]
• [4, 1]
• [3, 2]
• [3, 1, 1]
• [2, 2, 1]
• [2, 1, 1, 1]
• [1, 1, 1, 1, 1]

Thus, $P(5) = 7$. We denote by $P(n, k)$ the number of partitions of $n$ into $k$ parts. So we have $P(5, 1) = 1$, $P(5, 2) = 2$, $P(5, 3) = 2$, $P(5, 4) = 1$, $P(5, 5) = 1$.

The recurrence for partitions is:

$$P(n, k) = P(n-1, k-1) + P(n-k, k)$$

The idea is to consider a partition $p[1], p[2], \dots, p[k]$ of $n$ based on the final element:

• if $p[k] = 1$, then we get a smaller partition by removing the $k$th part, giving us a partition of $(n-1)$
  as $[p[1], p[2], \dots, p[k-1]]$. Here the number decreases from $n \mapsto (n-1)$ and the number of parts decreases from $k \mapsto (k-1)$.
• if $p[k] \neq 1$ (that is, $p[k] > 1$), then we get a partition of $n-k$ by knocking off a $1$ from each partition, giving us $[p[1] - 1, p[2] - 1, \dots, p[k]-1]$. Here we decrement on the number $n \mapsto n - k$ while still keeping the same number of parts.

References

• Bijective Combinatorics
• Slides by Brian Miceli

Stars and bars by direct bijection

We know that the number of $k$ element multisets using letters from ${1, \dots, n}$ is $\binom{k+n-1}{k}$. That is, we are allowed to pick elements from ${1, \dots, n}$ repeatedly, and we want $k$ such elements.

The usual proof: stars and bars

The usual proof involves creating $k$ "stars" ($\star$) which need to be placed in $n$ buckets. These buckets are created by having $(n-1)$ "bars" ($|$). For example, if we wish to consider all $k=3$ element multisets of the letter $n=4$: ${w, x, y, z}$:

$$ \begin{aligned} &[w, w, w] \mapsto \star \star \star \vert \vert \vert \ &[w, x, y] \mapsto \star \vert \star \vert \star \vert \ &[x, x, x] \mapsto \vert \star \star \star \vert \vert \ &[x, z, z] \mapsto \star \vert \vert \star \star \ \end{aligned} $$

Direct bijection.

To build a direct bijection, map a $k$ multiset of $n$ into a $k$ subset of $n+k-1$, which is counted by $\binom{n+k-1}{k}$.

• We are first given a $k=6$ multiset of $n=3$, say $m = {3, 1, 2, 1, 3, 3}$ ($m$ for multiset).
• We make the representation unique by imposing an ascending order, so we write $M = [1, 1, 2, 3, 3]$, where each $M[i] \leq M[i+1]$.
• Now, we map the above sequence to a set of unique values, by mapping $N[i] = M[i] + i$. Since $M[i] \leq M[i+1]$ we have that $M[i] + i < M[i+1] + (i+1)$.
• This gives us the set $M' = { 1+0, 1+1, 2+2, 3+3, 3+4 } = { 1, 2, 3, 6, 7 }$.
• See that this process is reversible. Given some set, say $N = { 4, 3, 2, 6, 7, 8 }$, order in ascending order to get $N' = [2, 3, 4, 6, 8]$ and then subtract $i$ from $N'[i]$ to get $[2-0, 3-1, 4-2, 6-3, 7-4, 8-5] = [2, 2, 2, 3, 3, 3]$.

I found this very elegant, because it "de-multisets" the multiset by adding just enough to make each element unique, and then simply counts the unique subset. Very slick! We need to add $k-1$ to the final index, and the largest number we can have is $n$ so we need $n + (k-1)$ values. We need a size $k$ multiset, making us need $\binom{n+(k-1)}{k}$.

• Reference: Bijective Combinatorics

DFS and topological sorting

The proper way to solve a maze is to keep breadcrumbs! Use recursion. Recursively explore the graph, backtracking as necessary.

DFS on a component:

parent = { s: None}
dfs-visit(adj, s):
  for v in adj[s]:
    if v not in parent:
      parent[v] = s
      dfs-visit(adj, v)

visit all vertices:

dfs(vs, adj):
  parent = {}
  for s in vs:
    if s not in parent:
    parent[s] = None
    dfs-visit(adj, s)

Complexity

We call dfs-visit once per vertex $V$. Per vertex, we pay adj(v) per vertex v. In total, we visit |E|.

Shortest paths?

DFS does not take the shortest path to get to a node. If you want shortest paths (in an unweighted graph), use BFS.

Edge classification

1. Tree edges: visit a new vertex via that edge. Parent pointers track tree edges.
2. forward edges: goes from node n to descendant of node n.
3. backward edges: goes from a node n to an ancestor of node n.
4. cross edges: all other edges. Between two non-ancestor-related nodes.

How do we know forward, back, cross edges?

Computing edge classifications

• backward edges: mark nodes being processed. if we see an edge towards a node still being processed, it's a backward edge.
• forward edges/cross edges: use time.

Which of these can exist in an undirected graph?

• Tree edges do exist. They better! That's how we visit new nodes.
• Forward edges: can't happen, because we will always traverse "backwards".

A ----> B
  ----> C

A -> C is a forward edge! If we made the above undirected, then we will have A -> B tree edge and B -> C back-edge.

• Back-edges: can exist in an undirected graph as shown above; B -> C is a back edge.
• Cross-edges: once again, cross edges can only come up from "wrongly directed" edges. But we don't have directions in an undirected graph.

Cycle detection

$G$ has a cycle iff $G$'s DFS has a back-edge.

Proof: DFS has a back edge => $G$ has a cycle

  tree
A -...-> X
^         |       
---back---*

By definition, A -> X is connected using tree edges, and a back edge X -> A. gives us the cycle.

Proof: $G$ has a cycle => DFS has a back edge

Say we have a cycle made of k vertices x, y, z, .... assume v[0] is the first vertex in the cycle visited by the DFS. Keep labeling based on how DFS visits then as v[1], v[2], ... v[k]. The we claim the edge v[k] -> v[0] will be a backedge.

• We know that when we're recursing on v[0], we will visit v[1] before we finish v[0].
• Similarly, v[i] will be visited before v[i-1].
• Chaining, we will finish v[k] before we finish v[0].
• In terms of balanced parens, it's like {0 (k; k) 0}.
• So, when we look at the edge v[k] -> v[0], we have not yet finished v[0]. Thus, we get a backedge.

Topological sort

Given a DAG, order vertices so that all edges point from lower order to higher order. The algorithm is to run DFS and output the reverse order of finishing time of vertices. Why does this work?

Proof that topological sort works

We want to show that for an edge $(u, v)$ that $v$ finishes before $u$, so that $v$ is ordered after $u$. Remember that we sort based on reverse of finishing order.

Case 1: u starts before v

We will eventually visit v in the recursion for u because u -> v is an edge. So, we will have the bracketing {u (v; v) u} so we're good: we finish v before we finish u.

Case 2: v starts before u

We have the bracketing (v ... {u. If we were to finish u before finishing v, then v is an ancestor of u, and this gives the bracketing (v .. {u .. u} .. v) and thus the edge $(u, v)$ is a back-edge. But this is impossible because the graph cannot have cycles! Thus, we will still have that v finishes beofre u, giving the bracketing (v v) .. {u u}.

• MIT introduction to algorithms: Lecture 14, DFS and topological sorting

Tournaments

• Tournament graph: either $U$ beats $V$, so we have $U \rightarrow V$ or we have $V$ beats $U$ so we have the edges $V \rightarrow U$ for every $U, V$

[image at 49:00 from video math for comp sci lecture 10]

• Example: A -> B -> D -> E -> C. Wait, C -> A. It's unclear how to talk about the best player!

directed Hamiltonian path

A directed walk that visits every vertex exactly once.

Theorem: every tournament graph contains a directed hamiltonian path

Induction on the number of nodes. When we start thinking of the problem, we have both nodes and edges as parameters. But edges are directly related to nodes, so it makes sense we induct on nodes.

Induction

If $n=1$ we are done. In the inductive step, assume it holds for $n=n$. For $n=n+1$, let's take out one node $v$ and see what happens. In the remaining graph, we still have a tournament graph on $n$ nodes. By the induction hypothesis we have a directed hamiltonian path $v_1 v_2 \dots v_n$. We want to create a bigger path that includes $v$.

Case 1

If $v \rightarrow v_1$ then we will get a path $v v_1 \dots v_n$.

Case 2

If $v_1 \rightarrow v$, then it is harder! Now what do we do? Ideally we want to plug $v$ somewhere in the sequence $v_1 v_2 \dots v_n$. Let's consider the smallest $i$ such that $v \rightarrow v_i$. We know that $i \neq 1$ as we are in case 2.

v1 -> ...v[i-1] -> v[i] -> ... vn
                   ^
                   v

If we have $v[i-1] \rightarrow v$ we are done because we get to insert $v$ into the path as $v[i-1] \rightarrow v \rightarrow v[i]$. Because $v[i]$ is the smallest index that $v$ beats, we must that $v[i-1]$ beats $v$ --- otherwise $i$ is no longer the smallest index!

Chicken tournament

Either a chicken $u$ pecks a chicken $v$ then $u \rightarrow v$ or the other direction, $v \rightarrow u$. We say that $u$ virtually pecks $v$ if there's a patch of pecking for $u$ to peck $v$.

The chicken king is the chicken that virtually pecks all other chickens.

We can have multiple king chickens. We want to find at least one chicken king. We may want to show that the vertex with the most number of outgoing edges
is going to be a king.

Theorem: chicken with highest out degree is the king

Proof by contradiction: assume $u$ has highest out degree and is not the king. So there is some vertex $v$ such that $\not u \rightarrow v$. Hence we have that $v \rightarrow u$. In the other case, we have that $\not u \rightarrow w \xrightarrow{\star} v$.

• Reference: Math for computer science, lecture 10

Matching problems (TODO)

Given a graph $G = (V, E)$ a matching is a collection of edges of $G$ where every node has degree 1.

Perfect matching

A matching is perfect if it has size $|V|/2$, or no vertex is left isolated. That is, everyone is matched with someone.

Weighted (Perfect) Matching

Some matchings maybe more preferable than orders, by giving weights.Usually, lower weights are more desirable. We may want to find the minimum weight matching. n The weight of a matching is the sum of the weights on the edges of $M$. In this context, we usually always ask for a perfect matching. Otherwise, one can trivially not match anyone to get a min-weight matching of weight 0. So the definition of a min-weight matching for the graph $G$ is a perfect matching with minimum weight.

We don't see these in 6.042. Will have to read flows/hungarian to study this.

Preference matching

Given a matching, $(x, y)$ form a rogue couple if they both prefer each other over their matched mates. Ie, they both wish to defect from their 'matched mates'. A matching is stable if there aren't any rogue couples. The goal is to find a perfect stable matching. That is, get everyone married up, and make it stable!

The point is, not everyone has to become happy! It's just that we don't allow rogue couples who can mutually get a benefit.

Bad situation for preference matching

If boys can love boys as well as girls, then we can get preference orderings where no stable marriage is possible. The idea is to create a love triangle.

• Alex prefers Bobby over Robin
• Bobby prefers Robin over Alex
• Robin prefers Alex over Bobby.
• And then there is mergatoid, who is the third choice for everyone. mergatoid's preferences don't matter

Theorem: there does not exist a stable matching for this graph

Proof: assume there does exist a stable matching, call it $M$. Mergatoid must be matched with someone. WLOG, assume mergatoid is matched to Alex by symmetry. If mergatoid is matched to alex, then we must have Robin matched to Bobby

• Alex and Bobby are not rogue, because Bobby likes Robin more than Alex.
• Alex and Robin are the rogue, because (1) Robin prefers Alex over Bobby, and (2) Alex prefers Robin over Mergatoid.

Hence, we found a rogue couple. So $M$ was not stable.

Stable Marriage Problem: success in some cases!

We have $N$ boys and $N$ girls [need the same number of each]. Each boy has his own ranked preference list of all the girls. Each gil has her own ranked preference list of all the boys. The lists are complete and there are no ties. We have to find a perfect matching with no rogue couples.

Mating algorithm / Mating ritual

The ritual takes place over several days.

• In the morning, the girl comes out to the balcony.
• Each boy goes to his favourite girl who hasn't been crossed off in his list and serenades her.
• In the afternoon, if a girl has suitors, she tells her favourite suitor "maybe I'll marry you, come back tomrrow". Girls don't make it too easy. For all the lower priority boys, she says "now way I'm marrying you".
• In the night, all the boys who heard a no cross that girl off from their list. If the boy heard a maybe, he will serenade her.
• If we encounter a day where every girl has at most one suitor, the algorithm terminates. So we don't have two or more boys under one balcony.

Things to prove

• Show that the algorithm terminates.
• Show that everyone gets married.
• Show that there are no rogue couples.
• We may want to show it runs quickly.
• Fairness? is this good for girls, or for boys?

Termination, terminates quickly: N^2 + 1 days

Proof by contradiction. suppose TMA does not terminate in $N^2+1$ days.

Claim If we don't terminate on a day, then that's because a girl had two or more boys under her balcony. Thus, at least one boy crosses the girl off of his list. We measure progress by the cross-out. In $N^2$ days, all boys would have crossed out all girls.

Invariant

• P is that if a girl $G$ every rejected a boy $B$ then she has a suitor who she prefers to $B$.

• To prove that this is indeed an invariant, induction on time. At the beginning, no girl has rejected any boy, so it's vacuously true.

• Assume P holds at the end of day $d$. At the end of day $d+1$, there's two cases.

• If $G$ rejects $B$ on day $d+1$, there must be a better boy, hence P is true.

• If $G$ rejected $B$ on day less than $d+1$, then $G$ must have had a better suitor $B'$ on day $d$ by the induction hypothesis. Now on day $d+1$, she either has $B'$ or someone even better, $B''$ came along.

Everyone is married

Proof by contradiction. Assume not everyone was married. Assume that some boy $B$ is not married. (If there is no boy who is not married then everyone is married).

• If we was not married at the end, then he must be rejected by everyone.
• If he were not rejected by everyone, then he would be under someone's balcony trying to serenade them. That he is unmatched means that all the girls have rejected him.
• This means that every girl has somebody better than $B$, which is not possible, because that would mean that every girl was married. That's not possible as there are an equal number of boys and girls.

Sid note: I don't buy this! we need to show that in the course of the algorithm, it's impossible for a girl to end up empty handed. I'd prove this by noticing that at each round, a girl acts like some kind of "gated compare and swap" where only the highest value is allowed to be put into the mutex, and all of the others are rejected. Thus, if there is a girl who has multiple writes, she will only allow one of the writes to happen, and permanently disallow the other writes. Thus, the other writes have to move to other girls.

No rogue couples

Contradiction: assume that there is a pair that are not married, call them bob and gail. We need to show that they will not go rogue. Since bob and gail are not married, either (1) gail rejected bob, or (2) gail did not reject bob because bob never serenaded her. If bob had serenaded her and was not rejected, then they would have been married!.

• (1) If gail rejected bob, then gail has marries someone she likes better than bob since she's rejected bob. Thus, gail and bob can't be a rogue couple because she likes her spouse more than bob.

• (2) bob never serenaded gail. This means that he married someone who he prefers more than gail, cause he never reached gail.

Fairness

• The girls get to pick the best ones who come to them.
• The boys get to go out and try their first choice though. A girl may wait for her Mr. Right who will never come along, and thus satisfice.
• Which is better? proposors or acceptors? Sociological question! Here it turns out that boys have all the power.
• Let $S$ be the set of all stable matchings. We know that $S$ is not empty because the algorithm is able to produce at least one stable matching.
• For each person $P$, we define the realm of possibility for $P$ to be the set $Q$ of people that they can be matched to in a stable matching. So $Q_p \equiv { q : (p, q) \in M, M \in S }$. That is, there's a stable marriage where you're married to them.
• A person's optimal mate is their most favourite in the realm of possibility. Their pessimal mate is their least favourite in the realm of possibility.

Theorem: No two boys can have the same optimal mate.

Assume two boys do have the same optimal mate. Say $(b^\star, g)$ and $(b, g)$. WLOG let $g$ prefer $b^\star$ over $b$. Now, there exists some "stable matching" where $g$ is matched with $b$, because $g$ is the optimal mate, hence in the realm of possibility of $b$. However, this matching is unstable because $(b^\star, g)$ is a rogue couple: $g$ likes $b^\star$ more than $b$, and $b^\star$ likes $g$ best!

Theorem: No two girls can have the same optimal mate

Redo previous proof by switching girl and boy. It's not a proof about the algorithm, but about the structure of stable matches themselves.

Theorem: The algorithm matches every boy with his optimal mate

Proof by contradiction. Assume that Nicole is optimal for Keith, but Keith winds up not marrying Nicole. This means he must have crossed off Nicole in some day (bad day).

Note that he must have gotten to Nicole, because no girls he prefers over nicole would have led to a stable marriage, and would thus not be an output generated by the algorithm. This, all girls he prefers above nicole must reject him at some step of the algorithm till he reaches Nicole.

We assume that in this instance of the algorithm, he does not get Nicole, thus Nicole too must have rejected him.

Let us assume that Keith gets rejected by Nicole on the earliest bad day.

When Nicole rejects Keith, this means that Nicole had a suitor she likes better than Keith. Call him Tom. Tom >Nicole Keith. Furthermore, since this is the earliest bad day, tom has not crossed off his optimal girl, and thus nicole must be the "best girl" for tom --- either out of his league, or the optimal feasible math. Thus, Nicole >Tom optimal-feasible-mate-for-tom.

But this means that in a stable marriage with (Nicole, Keith), we would have (Nicole, Tom) be a rogue couple! This contradicts the fact that nicole is optimal for keith.

• Proof from Optimal Stable Matching Video, MIT 6.042J Mathematics for Computer Science, Spring 2015.

We match every girl with her pessimal mate

TODO

Theorem: matchings form a lattice

Let $M = ((b_1, g_1), (b_2, g_2), \dots (b_n, g_n))$ and $M' = ((b_1, g'_1), (b_2, g'_2), \dots, (b_n, g'_n))$ be two stable matchings. Then.

$$ M \lor M' \equiv ((b_1, \max_{b_1}(g_1, g_1'), \dots, (b_n, \max_{b_n}(g_n, g_n'))) $$

is a stable matching.

Step 1: This is a matching

First we show that it is indeed a matching: the marriages are all monogamous. Assume that we had $g_1 = \max_{b_1}(g_1, g_1') = \max_{b_2}(g_2, g_2') = g_2'$.

Since $(b_2, g_2')$ is the match in $M'$ and $g_1 = g_2'$, we have that $(b_2, g_1)$ is the match in $M'$. We also know that $g_1 >{b_1} g_1'$ from the assumption. Since the matching $M'$ is stable, we need to ensure that $(g_1, b_1)$ is not a rogue couple; $b_1$ prefers $g_1$ over $g_1'$. Thus, we must have that $b_2 >{g_1} b_1$ to ensure that $(b_2, g_1)$ is stable.

However $M$ is stable, and $(b_1, g_1) \in M$. Since we have that $b_2 >_{g_1} b_1$, for $(b_1, g_1)$ to be stable, we must ensure that $(b_2, g_1)$ is not a rogue couple, since $g_1$ prefers $b_2$ over $b_1$. This we must have that $g'1 >{b_2} g_1$.

But this contradicts the equation $\max{b_2}(g_2, g_2') = g_2' = g_1$ (?)

Sid musings

the girls are monotonic filters, where they only allow themselves to match higher. The propogate (in the kmett/propogators sense of the word) information to all lower requests that they will not match. The boys are in some kind of atomic write framework with conflict resolution, where a girl allows a boy to "write" into her 'consider this boy' state if the boy is accepted by her filter.

References

• MIT OCW Math for comp sci: lecture 7 --- matching
• SPOJ problem
• Knuth: Stable matching and its relation to other combinatorial problems
• Math for Comp Sci: Optimal stable matching

Four fundamental subspaces

• Column space / Image: $C(A)$, since it corresponds to $C(A) \equiv { y : \exists x, y = Ax }$
• Null space $N(A) \equiv { k : Ak = 0 }$.
• Row space: row spans the row space, so it's all linear combinations of the rows of $A$. This is the same as all combinations of the columns of $A^T$. Row space is denoted by $C(A^T)$.
• Null space of $A^T$: $N(A^T)$, also called as the "left null-space of $A$".

Let $A$ be $m \times n$. The Null space of $A$ is in $\mathbb R^n$. The column space is in $\mathbb R^m$. The rows of $A$ are in $\mathbb R^n$. The nullspace of $A^T$ is in $\mathbb R^m$.

We want a basis for each of those spaces, and what are their dimensions?

• The dimension of the column space is the rank $r$.
• The dimension of the row space is also the rank $r$.
• The dimension of the nullspace is $n - r$.
• Similarly, the left nullspace must be $m - r$.

Basis for the column space

The basis is the pivot columns, and the rank is $r$.

Basis for the row space

$C(R) \neq C(A)$. Row operations do not preserve the column space, though they have the same row space. The basis for the row space of $A$ and $R$ since they both have the space row space, we just read off the first $r$ rows of $R$.

Basis for null space

The basis will be the special solutions. Lives in $\mathbb R^n$

Basis for left null space

It has vectors $y$ such that $A^T y = 0$. We can equally write this as $y^T A = 0$. Can we infer what the basis for the left null space is from the process that took us from $A$ to $R$? If we perform gauss-jordan, so we compute the reduced row echelon form of $[A_{m\times n} I_{m \times m}]$, we're going to get $[R E]$ where $E$ is whatever the identity matrix became.

Since the row reduction steps is equivalent to multiplying by some matrix $M$, we must have that:

$$ \begin{aligned} &M [AI] = [RE] \ &MA = R; MI = E \implies M = E \end{aligned} $$

So the matrix that takes $A$ to $R$ is $E$! We can find the basis for the left nullspace by lookinag at $E$, because $E$ gives us $EA = R$.

Reference

• Gilbert strang, lecture 10: four fundamental subspaces

WHO list of essential medicines (WIP)

• Wikipedia reference

why is int i = i allowed in C++?

This bizarre program:

struct Foo { explicit Foo() {}; }
int main() { Foo foo = foo; cout << "works!"; return 0; }

actually works! Why is this allowed? The only real use-case I know for this is to write:

const int ARRSIZE = 200;
int *ptr = malloc(sizeof(ptr) * ARRSIZE);

Still, this seems awfully dodgy. It feels like the C speficiation could allow the use of the left-hand-side name in expression that only need type information while emitting compile time errors for expressions that use the left-hand-side-name as a value.

Kakoune cheatsheet

• /: search for some text. n: go to next occurence. Shift-n: goto next occurence with a multi cursor.
• Shift-X: select multiple lines in sequence. s: make a multi-cursor a word in the current selection
• space: remove multiple cursors
• Alt+i <key>: select <object> of some type. Example: Alt+i w: select word. Alt+i s: select sentence.
• Shift-c: create multiple cursor in line below
• X: select line.

Assembly IDE

I've wanted to "learn assembly" properly, in the sense of write small to medium programs to feel like a native. Scouting around for IDE's, I couldn't find much. However, it seems like emacs has a rich ecosystem for assembly! I had no idea if it's a good ecosystem --- my experience with emacs has been hit and miss. I decided to take the dive.

• http://ref.x86asm.net/
• nasmshell
• nasm-mode
• x86-lookup
• blog post
• link to volume 2
• Link to general page with download link called as Intel 64 and IA-32 architectures software developer's manual combined volumes 2A, 2B, 2C, and 2D: Instruction set reference, A-Z.
• cgasm to quickly lookup assembly.

Cohomology is like holism

A shower thought, but Cohomology is indeed like holism. It describes precisely how the whole is greater than the sum of its parts, in terms of capturing a "global defect" that is oftentimes "locally trivial".

Flows (WIP)

• Srinivas Devdas: Flows

Canonical Transformation

• No self loops.
• No loops of the form s -> u -> s. (ie, no 2-vertex loops).
• This allows us to conflate "positive flow" and "net flow".

Notation: Net flow / flow

• A flow on $G$ is a function $f: V \times V \rightarrow \mathbb R$ such that $f(u, v) \leq c(u, v)$ for all vertices $u, v$.
• Flow conservation: for all vertices $u$, $\sum_v f(u, v) = 0$.
• anti-symmetry: $f(u, v) = -f(v, u)$.

Implicit summation notation

The value of a flow $f$ denoted as $|f|$ (cardinality of $f$), is denoted as:

$$ |f| \equiv f(s, V) = \sum_v f(s, v) $$

Properties of flow

• $f(X, X) = 0$. $f(a, a) = 0$ because self loops are not allowed. for two different vertices, we're going to get $f(a, b) + f(b, a) = 0$ by skew symmetry. In general, $f(X, Y) = -f(Y, X)$.
• $f(X \cup Y, Z) = f(X, Z) \cup f(Y, Z)$ if $X \cap Y = \emptyset$.

Theorem: $|f| equiv f(s, V) = f(V, t)$

Recall that $|f| = f(s, V)$. We want to show that $|f| = f(s, V) = f(V, t)$. So whatever gets pushed out gets pushed in.

$$ \begin{aligned} &|f| \equiv f(s, V) \ & f(s, V) + f(V - s, V) = f(V, V) = 0 \ & f(s, V) = f(V - s, V) \ & f(s, V) = f(V - s - t, V) + f(t, V) \ & f(s, V) = f(t, V) - f(V - s - t, V)\ & [\text{any vertex in $V - s - t$ is an intermediate vertex, which has 0 net flow}] \ & f(s, V) = f(t, V) - 0 \ & f(s, V) = f(t, V) \ \end{aligned} $$

Cut:

A partition of the network into two parts, such that the source is in one part and sink in the other. $(S, T)$ is a cut of a flow network $G$ is a partition of $V$ such that $s \in S, t \in T$. If $f$ is a flow on $G$ then the flow across the cut is $f(S, T)$.

Capacity of a cut and its relationship to flow

$$c(S, T) = \sum_{s \in S, t \in T} c(s, t)$$ See that we only get positive coefficents here. There is no "negative capacity", only "negative flow".

Theorem: upper bound flow across a cut

Value of any flow is upeer bounded by the capacity of any cut. We need more tools to prove this, as this is basically max-flow-min-cut

A different characterization of flow value

Lemma: for any flow $f$ and any cut $(S, T)$ we have that $|f| = f(S, T)$. It's because we have the source on one side, and the sink on the other side. That gives us the flow! Everything else cancels by conservation.

$$ \begin{aligned} &f(S, T) = f(S, V) - f(S, S) \ &f(S, T) = f(S, V) - 0 \ &f(S, T) = f(s, V) + f(S - s, V) \ \end{aligned} $$

As $S - s$ does not contain $t$, by flow conservation, we must have that $f(S - s, V) = 0$. Thus we get:

$$ \begin{aligned} f(S, T) = f(s, V) = |f| \end{aligned} $$

So, I can know the capacity of any cut $(S, T)$ bounds the flow of the network! So if I go look at the min-cut, then I can bound the max flow. We don't know how to find these min-cuts. That's what we'll need to figure out.

Residual network

Network that points us to locations with leftover capacity where we can push flow. $G_f(V, E_f)$ contains all those edges that have positive (greater than zero) residual capacity. Edges in $E_f$ admit more flow. If $(v, u) \not \in E$, then $c(v, u) = 0$, but $f(v, u) = -f(u, v)$. So we will have extra edges in the residual network that don't exist in the original network.

If I have a flow $-1$ due to a back-edge with capacity $0$, I can in fact send more flow to make it $0$! So I can have "back edges" in the residual network for edges whose flow has to shrink.

Augmenting path in $G_f$

Sid question: A path from $s$ to $t$ in $G_f$. Why does the existence of an augmenting path in $G_f$ actually mean that we can increase the flow? even when we have "back edges"? Sid answer: Because at the end of the day, we are picking a path from $s$ to $t$ which tells us how to change our flow in a way that we still respect capacity constraints.

Amortized analysis

• Erik Demaine: amortization --- amortized analysis

Table doubling

• Expected cost of hash lookup: $O(1 + n/m)$ where $n$ items in table of size $m$ ($n/m$ is the load factor)
• Total cost for $n$ insertions: $2^0 + 2^1 + \dots + 2^{\log n} \simeq O(n)$.
• Amortized cost per operation is $O(1)$.

Aggregate method

We do some sequence of $k$ operations. Measure the total cost of the $k$ operations and divide by $k$. This defines the amortized cost (Weak definition).

Generalized definition (amortized cost)

• assign some cost for each operation, called the amortized cost, such that it "preserves the sum" of the cost for all operation sequences op[i].

$$ \begin{aligned} \sum \texttt{amortized-cost}(op[i]) \geq \sum \texttt{real-cost}(op[i]) \end{aligned} $$

• The cost that obeys this inequality is called as the amortized cost.

2/3 trees:

• O(1) to create

• O(log n) to insert (amortized)

• O(0) to delete? (amortized) We can bound the deletion cost by the insertion cost, because we can't delete more items than we have inserted! We can bound the delete cost by the insert cost.

• c creation time, i insertions, d deletions.

• Let $n^\star$ be the largest size of the tree we've encountered in this sequence of operations. This way, we are really bounding the worst case.

• The real cost is $(c + i \log n^\star + d \log n^\star)$. Let's try to show an amortized bound with O(0) to delete!.

$$ \begin{aligned} &O(c + i \log n^\star + d \log n^\star) \ &= O(c + (i + d) \log n^\star) \ &[\text{$d \leq i$ since we can delete at most number of items}] \ &\leq O(c + 2i \log n^\star) \ &\leq O(c + i \log n^\star) &\leq O(c + i \log n^\star + 0d) \end{aligned} $$

Accounting method

Define a time bank account. An operation can store time credit in that bank account. Bank account must always have non-negative time balance. Performing operations costs time. So we can either directly pay for operations, or we can pull money from the time bank account. We can pay for time using the stored credit in the bank.

Sid note

On the whole I always find this confusing; Why would I have a bank account if I can also simultaneously pay with an infinite amount of money? So I prefer to think of it as me having (1) an infinitely large, slow, reservoir of gold, (2) a quick cache of gold [which replaces the "bank"]. To pay for an operation, I can only access money from my quick cache, because pulling money from my slow reservoir is slow. I can transfer money from my infinitely large reservoir to my quick cache of gold. The amortized method calculates the total amount of gold that was pulled from the reservoir and stored into the cache. We might have leftover gold in the quick cache (upper bound). We can't have "negative gold" in the cache. We define the amortized cost to be the total number of gold coins pulled out of infinite reservoir by an operation.

Accounting example: 2/3 trees

When we insert, I pull $2 \log(n^\star)$ from my reservoir. I use $1 \log(n^\star)$ to pay for the insertion, and keep a reserve of $\log(n^\star)$ in the bank. Then when we delete an element, we use the $\log(n^\star)$ extra we had kept in the cache from the insert.

Better bounds: removing the star

We want to say that we pay $\log(n)$ for insert and delete where $n$ is the size of the tree when we perform the insert or delete.

Per insert, we pull in two gold coins worth $\log(n)$ from the reservoir into the cache. When we delete, we use the $\log(n)$ in the cache from the money that was withdrawn when we created that element. See that the $n$ changes as the size of the data structure changes.

Table doubling via accounting

• When we insert a item into a table, withdraw $c + O(1)$ value from the reservoir. Keep gold coin worth $c$ that was in the cache on the item that was inserted. So imagine a real gold coin worth $c$ floating above the item.

• When we double the size of the table, use up as many old coins as possible, and then withdraw the rest of the cost from the infinite gold reservoir. Also withdraw to keep coins on the newly inserted items.

• So by the time we double, half of the elements have coins, other half don't. At the end, I'm going to have $n/2$ coins. The amortized cost of doubling is going to be $O(n) - cn/2$ which is going to be zero if $c$ is large. since I will have $cn/2$ coins in my cache of gold.

• Insert costs $O(1 + c) = O(c)$ since we need to pull out those many coins from the infinite gold reservoir.

Charging method

Time travel/blame the past for your mistakes. We allow operations to charge their cost retroactively to their past (not to their future!). An operation can withdraw more value that it immediately needs from the infinite reservoir into the gold cache, and it keeps it "for itself" for future-itself.

• amortized cost = total gold pulled out of infinite reservoir.

Charging example: Table doubling

After we double the table, the table is half-full, we need to perform $n/2$ insertions to get the table to be full. When we double the array next time, we charge the doubling to the insertions since the last doubling! There are $n/2$ items since the last doubling (I had 2 items, I doubled to 4 items, so there are n/2 new items. Now I want to double and add 4 more items). I have a cost of O(n) for the doubling. So I can charge O(1) cost to all the new items since the last doubling. Note that I only charge once; after I've charged items, I've doubled the array, so they are now "old".

Charging example: Table doubling, inserts and deletes

(37:00 TODO)

Potential method (Most powerful) / Defining karma:

We define a potential function $\phi$ mapping a data-structure-configuration to an natural number pile of gold coins. It tries to measure how bad the datastructure is right now. We can pull money out of the pile of money in the potential. Amortized cost is the actual cost plus the change in the amount of money in the data structure configuration after and before:

$$ \texttt{amortized(op)} = \texttt{real(op)} + \phi(\texttt{after(op)}) - \phi(\texttt{before(op)}) $$

Adding up all the amortized costs, the sum telescopes, giving us

$$ \texttt{amortized(total)} = \texttt{real(total)} + \phi(\texttt{end}) - \phi(\texttt{begin}) $$

• We really like to have $\phi(\texttt{begin}) = 0$.

Potential example: binary counter

flipping a bit is $O(1)$. How much will increment cost? An increment is going to cost 1 + the number of trailing ones. We want to make this constant.

• What is making this bad? the number of trailing ones? Consider 11110 which has zero trailing ones. If I increment it I get 11111, which has 5 trailing ones. So I need to pull on 5 gold coins, which is O(n). No good, I want O(1). Though this is the natural thing to try, it doesn't quite work.

• Rather, we can define $\phi$ to be the total number of 1 bits. Whenever I increment, at maximum, I can add one 1. If a number has t trailing bits, then on incrementing, I destroy t one bits, and add a single one-bit. eg: 0110 + 1 = 1000.

• The amortized cost is: 1 + t (actual cost). The change in potential is: t - 1 [lost t 1s, gained 1 one]. So the amortized cost is total cost - change in potential, which is 1 + t - (t - 1) = 2, a constant.

Shelly Kegan: death --- Suicide and rationality (WIP)

How does the fact that we will die affect the way we live? previous chapter! The fact our mortality raises the question of whether or not we should put an end to our life. It's the extra feature --- the variability of death, the fact that we can control how long we live, and thus we face the possibility of ending our life earlier than it would otherwise. Under what circumstances is it a good thing to do?

You must be either crazy or immoral is the knee jerk. The very first thing to do is to distinguish questions of rationality from morality.

Rationality of suicide

1. When if ever would it be true that you are better off dead?

2. Assume that the answer to the first question is "under circumstance X,

   you would be better off dead", can you trust your judgement that this is one of those cases X?

In those circumstances that life is terrible, you can't think clearly. So perhaps you ought not attempt to make "rational decisions" under duress. Non existence is not a state because it depends on existence.

Dying would be bad because it would deprive us of the good things in life --- the deprivation requirement. If we believe in the two state requirement, how can we say this? The two state argument can't even tell us that it's better off to be alive for the happiest person! So the two state requirement is not a genuine requirement. We simply have to say that the life you would have had is a great life; I don't need to say anything about how death is going to be inferior. The "loss of a good state" is enough, without needing to know what we are transitioning into.

But if so, we can flip the argument by symmetry. If a person's life was full of suffering and misery and disappointment, then for their life to go longer would be bad.

What goes into making someone's life worthwhile? people disagree about the ingredients of the best kind of life. Going back to hedonism (add all pleasure, subtract all pain), if this number comes out negative, then your life is not worth living. The longer you live, the more the balance shifts to the negative (say).

Is life itself worth having? Neural container theory: life is a container in which good/bad is filled up. Valuable container theories: the very fact that you are alive gave you some positive value. Fantastic continer theories: doesn't matter how bad the contents get, even so the grand total is still positive. What's so incredible about life itself? They argue that being alive itself is valuable. But most people don't really mean life, they mean life as a person. For example, they would not agree that being alive as a blade of grass is a "good life".

What about a life where the person's functioning has decayed, but they can still feel pain? In that case perhaps, their life's quality can degrade.

We can probably find sympathy with the perspective that here on out, their life is going to be net negative; someone who has terminal cancer and is in great pain.

There could be a person where they're suffering from a degenerative diesease, but are still able to think and have a life worth living while slowly losing motor control. One day there comes a time when their life is not worth living, but by that point, they don't have control over their body.

It's easy to mistake a low point with a global minima; Even if life is less worth living than you hope it would be, it might feel terrible in the position.

Deciding under uncertainty

Could it ever be true that you're better off dead?

The very claim that "jones would be better off dead" can't make any sense. In order to make comparisons we need to be able to talk about states before and after. Call this the two state requirement.

Morality of suicide

• Shelly Kegan: death, 24. Suicide, Part 1

Sam harris and jordan peterson: Vancouver 1 (WIP)

Is there a difference between religious and non-religious totalitarian states? Yes, dogma is the commonality. In the case of stalin / north korea, they are almost religions that are not branded as "religions". ~ Sam

the problem with dogmas is that they do not allow revision. The moment someone has a better idea you have to shut it down. ~ Sam

Free speech elevates error correction of dogmas above dogmas. So Free speech must be on the pinnacle in the hierarchy of values ~ Peterson

The only problem with the religion is the dogmatism. I've got no problem with the buildings and the music and ... ~ Sam Harris.

What is the phenomenology of spiritual experience? That phenomenology is real! This phenomenology seems to confirm the dogma.

The core element of tribal alliance is independent of the religious substrate? Religion can allow clearly good people who are not captured by tribalism are able to perform atrocities. This suffering is not from a "ape like" urge. If you buy the claim that quran is the perfect word, then human rationality is bounded pathologically which leads to worrying outcomes.

Christians were the ones in egland who were against slavery ~ Petersen Yes, because they were the only ones around, so they must have done everything then ~ Sam Don't forget that the christians used their christian faith as an argument against slavery ~Petersen Well then it's unfortunate that they were on the losing side of an argument. If only the bible had said "don't keep slaves" imagine how much easier their movement would have been ~Sam.

Rise of postmodern interpretations of literature. Take a complex narrative, there are many ways of interpreting it. For example, consider a movie with a twist at the end. The twist changes the emaning of the entire movie. So while the bible may contain, sentence by sentence, things that are "just wrong" from a modern lens, perhaps it's not so when viewed holistically. Everything in a narraitve is conditioned on the entire text. While you may argue that some sentences in the bible are so horrific that it's impossible to use context to massage them, you have to give the devil his due. The Christian bible is a narrative.

OK, what does this do to Moses' laws of war and doctrines?

the notion of revelation and prophecy destroys a whole bunch of soceity. I've read to the end of the book, it's scary to the end as well!

there is an idea in the bible, that things are always going to be falling apart, there is an apocalyptic crux to everything touched by humanity. Hero is born in the darkest point in the journey. When things fall apart, that is the time of the hero.

You can read into any story psychological insights ~ Sam. But you can do that with any set of facts too ~ Peterson. This why fundamentalim has an edge over modern theology. Modern theology concedes that we can't read it literally. But the more you get away from the literal you can broadcast whatever you want.

This notion that redemption is to be found in truthful speech is embodied as a person. you want to ground values in something that is true. But the problem is that i can't see how you can inerpret the world of facts without an a priori structure.

Kant identified time and space as a priori intuitions. I claim that stories are another kind of a priori intuition. You can write down stories of utpoia and dystopia; When you do, you're already two thirds your way to heaven and hell. Why not go all the way?

Literal versus metaphorical truth. There are some truths that are literally false but if you behave as if they were true you come out ahead.

Imagine a universe where every possible mind is tuned to the worst possible experience that they can. If anything is bad, that's bad. If the word bad is going to mean anything, it's bad. I claim that this is a "factual claim". Every claim we make about anything, turtles all the way down, gets us to something that's bedrocked on intuition [Perhaps even math, in terms of the axioms we choose? Mh, I'm not very convinced, but sure]. If we are going to use the word bad and good, there will be an implicit acknowledgement that the worse possible misery for everyone is bad. It's built in. ~ Sam Jordan disagrees that this is a factual claim.

Why did people do the worst things

• Sam harris and jordan peterson: Vancouver 1

Correctness of binary search

Closed-closed intervals

// search in interval [l, r] for value `val`
int binsearch(int l, int r, int val, int *xs) {
  if (l == r) { return l; }
  int mid = (l+r)/2;
  if (xs[mid] <= val) { 
    return binsearch(l, mid, val, xs);
  } else {
    return binsearch(mid+1, r, val, xs);
  }
}

We have (l <= mid < r) since floor division of the form (l+r)/2 will pull values "downward". The length of the interval [l, mid] is smaller than the interval [l, r] as mid < r. The length of the interval [mid+1, r] is smaller than the interval [l, r] as l < mid+1. We are monotonically decreasing on the quantity "length of interval", and terminate the recursion when the length is zero.

Closed-open intervals

// search in interval [l, r) for value `val`
int binsearch(int l, int r, int val, int *xs) {
  // [l, l+1) = { l }
  if (r == l + 1) { return l; }
  int mid = (l+r)/2;
  if (xs[mid] <= val) { 
    return binsearch(l, mid, val, xs);
  } else {
    return binsearch(mid, r, val, xs);
  }
}

We have (l <= mid < r) since floor division of the form (l+r)/2 will pull values "downward". Furthermore, if r = l + 1 we end the recursion. Thus, we are guaranteed that we will have that r >= l + 2. Hence, mid = (l+r)/2 >= (l + l + 2)/2 >= l + 1. Thus, we have that: l is to the left of mid=l+1 is to the left of r>=l+2. So the intervals [l, mid) and [mid, r) will be smaller, as we cleanly "separate" out l, mid, and r.

readlink -f <path> to access file path

To get the full path of a file, use

$ readline -f file
/path/to/file

This is useful to scp/rsync stuff.

rank/select as compress/decompress

I haven't found a good naming convention so far for describing order statistics. I'm taking about the common implementation:

vector<int> xs(n);
vector<int> order2ix(n);
for(int i = 0; i < n; ++i) { order2ix[i] = i; }

sort(order2ix.begin(), order2ix.end(),
     [](int i, int j) {
        return make_pair(xs[i], i) < make_pair(xs[j], j);
     };

where order2ix[o] gives us the element with that order statistic. So, order2ix[0] contains the smallest element, order2ix[n-1] contains the largest element, etc. I've previously tried the naming conventions:

rank/select

rank: ix -> order, select: order -> ix. The pro of this is that it uses the rank/select naming convention. This leads into the Galois connection aspect of it, but is otherwise not so useful.

order2ix/ix2order

The signatures are order2ix: order -> ix, ix2order: ix -> order. This uses the order statistic naming convention, and thereby makes it clear what the query is: you tell me the kth order, I give you the index in the array in order2ix(k). Alternatively, you tell me the index i, and I'll tell you its order statistic in ix2order(k).

However, I found implementing this kind of odd. In particular, I need to pause for a second and think about what maps to what in the ix2order[order2ix[o]] = o;.

vector<int> xs(n);
vector<int> order2ix(n);
for(int i = 0; i < n; ++i) { order2ix[i] = i; }

sort(order2ix.begin(), order2ix.end(),
     [](int i, int j) {
        return make_pair(xs[i], i) < make_pair(xs[j], j);
     };

// REVERSE BIJECTION
vector<int> ix2order(n);
for(int o = 0; o < n; ++o) { ix2order[order2ix[o]] = i; }

For me, the major source of disconnect is that this "order" feels somewhat disconnected from the original array xs. So I feel like I'm trying to reason about these three

• The indexes 0, 1,..,n
• The orders 0th,1st,2nd,..(n-1)th
• The array values xs[0],xs[1],xs[2],..xs[n]

and it's unlclear to me how the two arrays order2ix and ix2order relate to each other.

compressed/decompressed:

Now for the new convention that I hope works better: compressed/decompressed:

The idea is that compressed maps the original numbers to their compressed variants. So it's going to have a signature compressed: ix -> smalluniv, where it compresses the element xs[i] into [0..n-1]. decompressed is the inverse function, which takes a number in the smaller universe, and returns its index in the original array. So we have decompressed: smalluniv -> ix.

Why I like this better

I feel this convention is superior, because it's intuitive to me at a glance as to what compressed/decompressed do and why they should be inverses. I feel it also matches the deep reason for why kth order statistic exists: it lets us perform universe reduction, to go from a large space of a total order to a small space [0..(n-1)].

Furthermore, the very name implies that compressed is the compressed version of something (the original array xs) and that decompressed is the decompressed version of something (the compressed universe [0..(n-1)]). This makes it clear how they're reated to the original array linguistically, which I quite like.

Remembering Eulerian and Hamiltonian cycles

I used to keep forgetting the difference. Here's how I remember it now. We know that an euler tour always exists for a tree. Indeed, it's a handy data structure that can be used to convet LCA (lowest common ancestor) into RMQ(range minimum query).

So, the "Euler tour" must exist for a tree. See that when we perform a tour on the tree, we definitely walk a vertex twice (once when entering, once when exiting). It seems like we walk the (undirected) edges twice as well. However, if we consider the edges as directed edges, then we're only walking the edges once.

• So an euler tour must correspond to a tour where we walk over each edge exactly once.
• A hamiltonian tour must (by complementarity) correspond to a tour where we over each vertex exactly once.

Nice way to loop over an array in reverse

const double n = sizeof(spheres) / sizeof(Sphere), inf = t = 1e20;
for (int i = int(n); i--; ) { } //chad
for (int i = n-1; i >= 0; i--) { // simp

Dynamic Programming: Erik Demaine's lectures

I realized I'd never bothered to ever formally learn dynamic programming, so I'm watching Erik Demaine's lectures and taking down notes here.

DP 1: Fibonacci, shortest paths

• Video lecture here

1. DP ~= careful brute force.
2. DP ~= subproblems + "recurse"

Fibonacci

F(1) = F(2) = 1; F(n) = F(n-1) + F(n-2)

Naive:

fib(n):
  if n <= 2: f = 1
  else f = fib(n-1) + fib(n-2)
  return f

EXPONENTIAL time! T(n) = T(n-1) + T(n-2) + O(1). Since it's the fibonacci recurrence, the solution is rougly $\phi^n$ where $\phi$ is the golden ratio. Alternate, T(n) >= 2T(n-2) ~ 2^(n/2)

Memoized DP:

memo = {}
fib(n):
  # vvv 
  if n in memo: return memo[n]
  if n <= 2: f = 1
  else f = fib(n-1) + fib(n-2)
  # ^^^
  memo[n] = f
  return f

• We can think about it in terms of the recursion tree, where this allows us to not have to recompute some of the data.
• The alternative way of thinking about it is that there are two ways of calling fib: the first time, it's non-memoized, which recurses. Every other time, we're doing memoized calls that are constant time.
• The number of non memoized calls in n. These we have to pay for. The non recursive work per call is constant.
• Therefore, the running time is linear! Linear because there are n non memoized calls, and each of them cost constant time.
• In general, in DP, we memoize (remember) solutions to subproblems that help us solve the actual problem. So, DP = recursion + memo.
• Running time = number of different subproblems x time per subproblem. When we measure time per subproblem, we ignore recursive calls! (don't count recursions).

Bottom up DP algorithm

fib = {}
 -- | some thought for the loop
for k in range(1, n+1): 
  if k <= 2: f = 1
  else: f = fib[k-1] + fib[k-2]
  fib[k] = f

Order based on any topo sort of dependency DAG. From the bottom up perspective, we can decide how much we need to store based on how much state we need.

  *------------*
  |            v
f(n-2) f(n-1) f(n)
          |    ^
          *----*

Single Source Shortest paths (s-v path)

• Tool to find answers: guessing. Suppose you don't know it. how do you find the answer? guess! Don't try any guess, try all guesses! (then take the best one).
• DP = recursion + memoization + guessing.

There is some hypothetical path from s to v. We don't know what the first edge of this hypothetical path is, so we guess. We try all of the paths from s->s'. This changes s, but we really care about single source shortest path. So rather, we choose to guess v. We guess the last edge u? -> v. Recursively compute the path from s to u?, and then add the path to v.

\delta(s, v) = \min_{(u,v) \in E} \delta(s, u) + w(u, v)

Subpaths of shortest paths are shortest paths! Memoize to make it fast? Why is it faster on memoization?

*---a----*
v   ^    v
s   |    w
|   |    |
*-->b<---*

δ(s, w) 
  δ(s, a)
     δ(s, b)
       δ(s, s)
       δ(s, w) <- INFINITE

• Infinite time on graphs with cycles.
• For a DAG, it runs on V+E. Number of subproblems = V. Time we spend per subproblem at a vertex is the number of incoming edges. we can't take product, because the time per subproblem can vary wildly. So we restate our "time formula" as

total time = sum over times of all subproblems (modulo recursion)

This gives us:

total time = sum indeg(v) + O(1) = O(E) + O(1)

• LESSON LEARNT: subproblem dependencies should be acyclic!

• Claim: can use same approach for graphs! Explode a cycle over time. This makes any graph acyclic.

Sid question: Can we derive Djikstras using the same "cycle explosion" trick?

We define $\delta_k(s, v)$ to be weight of shortest path that uses at most k edges.

\delta_k(s, v) = \min_{(u, v) \in E} \delta_{k-1}(s, u) + w(u, v)

We've increased the number of subproblems. We know that the longest path possible can have $|V| - 1$ edges. So the k parameter goes from [0..|V|-1] while the vertex v can be any vertex. Per vertex v we spend indeg(v) time. So we get the total recurrence as:

$$ \begin{aligned} &\sum_{(k \in [|V|-1], v \in V)} T(k, v) = \ &\sum_{k \in [|V|-1]} \sum_v indeg(v) = \sum_{k \in [|V|-1]} E = VE \end{aligned} $$

DP 2: Text Justification, Blackjack

• Video Lecture

5 "easy" steps to a DP

1. Define subproblems; analysis - number of subproblems
2. Guess (part of solution); analysis - number of choices for the guess
3. Relate subproblem solutions [with a recurrence]; analysis - time per subproblem (ignoring recursion)
4. Build an algorithm: [recursion/memo, or tabling]; check recurrence is acyclic
5. solve original problem; total time: total time across all subproblems (ignoring recursion). In simple cases, total time = number of subproblems x time per subproblem.
6. Check that the original problem actually gets solved!

Recap: Fibonacci

1. subproblems: F(1)...F(n)
2. guess: nothing
3. relate: F(n) = F(n-1) + F(n-2); O(1) time
4. F(n). constant time to find

Recap: Shortest path

1. subproblems: $\delta_k(s, v)$. $V^2$ subproblems.
2. guess: last edge; edge into $v$.
3. relate: $\delta_k(s, v) = \min_u \delta_{k-1}(s, u) + w(u, v)$; indegree(v) time
5. $\delta_{v-1}(s, v)$ for all $v$. This takes $\Theta(V)$.

Text Justification

split text into "good lines". can only cut between word boundaries. Text is a list of words. badness(i, j): how bad is it to use words[i:j] in a line. They may fit, or they may not fit. If they don't fit, then badness is ∞. Otherwise, it's going to be (pagewidth - total width)^3. We want to minimize the sum of badnesses of the lines.

1. subproblems: the hard part! exponential: Guess for every word, whether a line begins or not. What is the natural thing to guess? guess how long the first line is / guess where the second line begins. After I guess where the second line is, I now have the remaining words to text justify. So the subproblems are going to be suffixes of the array: words[i:]. If we have n words, we have n suffixes. We're going to only remember one line [forget the past!], not all the lines! [this is exponential!]
2. Guess: where to start the second line. If we are at location i, there are n-i choices which we will think of as O(n).
3. Recurrence: $dp[i] = \min{i+1 \leq j \leq n} \texttt{badness}(\texttt{words[i:j]}) + dp[j]$. Time per subproblem is constant x [i+1..n] which is O(n).
4. Check recurrence is acyclic/topo order: n, n-1, ... 1
5. Total time: number of subproblems x time per subproblem = O(n^2)
6. Original problem: dp[0].

Parent pointers

Remember which guess was best. Find actual solution, not just the cost of the

fiat

fiat lux.

Let there be light solution.

n suffixes | exp many sybsets. dont need to know history!

Blackjack

whatever, I don't particularly care about the game

DP 3: Paranthesization, Edit distance, knapsack

Sequences

Good choices of objects to perform DP on:

• Suffixes: x[i:] for all i. O(n).
• Prefixes: x[:j] for all j. O(n).
• Substrings: x[i:j] for all i and j. O(n^2).

Parenthesiztion

optimal order of associative expression.: A[0] . A[1] ... A[n-1]. Order matters for matmul!

• What should we guess? There are exponentially many parenthesizations! Guess the outermost/last multiplication. Ie, we want to know:

(A[0] ... A[k-1]) * (A[k] ... A[n-1])`

• We can't just use prefixes and suffies, because when we recurse into A[0]...A[k-1], we're going to get splits of the form A[0]...A[k'] and A[k']...A[k-1]. In general, if we feel we need both prefixes AND suffixes, we likely need the full power of substrings.
• So our choice of subproblem is: dp[i][j] is the optimal outermost split for A[i]...A[j-1] The number of choices is O(j-i+1) = O(n).

dp[i][j] = min{
  for k in range(i+1, j):
    dp[i][k] + dp[k][j] + cost of (A[i:k] * A[k:j])
}

• Time is polynomial. O(n) time for subproblem ignoring recursions. We have O(n^2) subproblems (substrings). So the running time is O(n^3).
• Topological order: in general, if we have prefixes, we go left to right. have suffixes, we go right to left. If we have substrings, we evaluate based on increasing substring lengths, since when we split, we get substrings with smaller lengths.

Edit distance

Given two strngs x and y. Find the cheapest way to convert x into y. We allow character edits to turn x into y: We can (1) insert a character anywhere in x, (2) delete a character anywhere in x, (3) edit any character in x. We have custom costs for each insert and delete.

• Can also solve longest common subsequence. HIEROGLYPOHOLOGY, MICHAELANGELO. Drop any set of letters from x and y, we want them to be equal. Model it as edit distance. Cost of insert/delete is 1, cost of replacement is 0 if characters are equal, ∞ otherwise.
• We will look at suffixes of x and y at the subproblem. Subproblem is edit distance on x[i:] AND y[j:]. Number of subproblems is $O(|x| |y|)$.
• We need to guess! Not so obvious. Look at the first characters. What can I do with the first character of x? (1) I can replace the first characters. (2) I can insert the character y[j] into x. (3) I can delete the character x[i]. So we have:

1. Replace x[i] with y[j].
2. Insert y[j].
3. Delete x[i].

dp[i][j] = min{
  cost of replace x[i] with y[j] + dp[i+1, j+1],
  cost of insert y[j] + dp[i][j+1],
  cost of delete x[i] + dp[i+1][j],
}

The topological order is going to have smaller to larger suffixes.

What I found really interesting is the offhand remark that longest common substring is just edit distance where we are allowed to only delete or keep characters.

Knapsack

List of items, each of size s[i] and a desire/value v[i]. The sizes are integers. We have a backpack of total size S. We want to choose a subset of the items which maximize the value, and also fit into the backpack: $\sum s[i] \leq S$.

• Even though it seems like we don't have a sequence, we have a set of items we can put in any sequence. We can look at sequences of items. At the item i, we should guess if item i is included or not.

# v WRONG
dp[i] = ... max(dp[i+1], dp[i+1] + v[i])`

We don't keep track of the sizes! Rather, we choose our subproblem to be the suffix AND the remaining capacity $x \leq S$. We have $O(n S)$ subproblems

# v correct
dp[i][s] = max(dp[i+1][s], dp[i+1][s-s[i]] + v[i])

To be polynomial in the input, it would have to be $\theta(n \log S)$ because $S$ is given as a number. It would not be $nS$; $S$ is exponential in the input encoding $\log S$.

R21: DP: Knapsack

We have n decisions: d[i] is do I take item i. What do we need to keep track of? I need to know how much weight I have left. This is equivalent to knowing the sum of the items. The edge is an arbitrary item, the weight is -v[i] since we're trying to phrase the problem in terms of shortest path. The state in the node is item I'm looking at, and weight of the items I've taken so far.

$$ \begin{matrix} \end{matrix} $$

DP4: Guitar fingering, tetris, super mario bros

A second kind of guessing. Guessing usually which subproblem to use to solve a bigger subproblem. Another way of guessing is to add more subproblems to guess or remember more features of the solution.

Mapping to knapsack

obvious solution was suffix in knapsack. So we needed to know how many units of the knapsack we've used up; we're remembering something about the prefix (but not the full prefix itself). On the other hand, in the forward direction, we were solving more types of subproblems, for varying sizes of knapsacks.

Piano and guitar fingering: Take 1

Given some musical piece to play: a sequence of n notes we want to play. We want to find a fingering for each note. We have fingers 1 upto f. We want to assign a finger to each note. We have a difficulty measure d(p, f, p', f'): how hard is to transition from note p (p for pitch) with finger f to note p' with finger f'?

• Subproblems: prefixes? suffixes? substrings? Suffixes are kind of fine. How to play notes n[i:].
• Guess: Which finger to put on note i?
• Recurrence:

dp[i] = min({ 
   for f in fingers:
      dp[i+1] + d(i, f, i+1, ?) # WRONG: don't know ?
})

• Add more subproblems! how to play notes[i:] when using finger f for notes[i].
• What to guess? finger g for note (i+1)

dp[i][f] = min({
  for g in fingers:
      dp[i+1][g] + d[notes[i], f, notes[i+1], g]
}

• Topological order:

for i reversed(range(n)):
   for f in range(F): ...

• Original problem: we don't know what finger to use for dp[0]. So we can take a min over all fingers. min([ dp[0][f] for f in range(F)])

guitar chords:

Generalize the notion of "finger" to "finger(F) + string(S)". This gives us $O(N((F+S)^2)) = O(NF^2S^2)$. Multiple notes: notes[i] = list of F notes for a piano.

• state: we need to know about the assignment of fingers to notes (or no note). So that's $(N+1)^F$. Generalize the rest.

Tetris

We know the entire sequence of pieces that's going to fall. For each, we must drop the piece from the top. Also, full rows don't clear. The width of the board is small. The board is initially emoty. Can you survive?

The subproblems are how to play suffixes of pieces[i:]. We need to know what the board looks like. If the board doesn't clear and we always drop from the top, then all we need to know is the skyline.

1| ###
2| #
3|####
4|####
5|####

• So we also store the board skyline. We have h different choices for each column. There are w columns. So we have (h+1)^w number of choices for skylines. Total number of subproblems is n.(h+1)^w.

• Guess: what do I do with piece i? I can rotate it 0, 1, 2, 3 times, and the where to drop it. I can guess where to drop the piece. This is 4w choices --- 4 for rotation, w for where we drop.

• Here the answer is a boolean: survive (1) or not (0). we want to survive, so we can just use max on a boolean.

Super Mario Bros

Recall that in the original super mario bros, if something moves out of the screen it's lost forever; We can't move back in the old mario. We're given the level, and a small $w\times h$ screen. The configuration of the game is everything on the screen! Total info is going to be $c^{wh}$ where c is some constant. We also need Mario's velocity, the score, and time. score can be S big, time can be T big. The number of configurations is the product of all of these. We also need to know how far to the right we have gone, which is another W. Draw a graph of all configurations, and then use DP

Lecture 10: Advanced DP by Srinivas

• Video

Longest palindromic sequence

Find palindrome inside longer word. Given a string X[1..n]. Find longest palindrome that is a subsequence.

character
c arac

answer will be greater than or equal to 1 in length because a single letter is a palindrome.

turboventilator
  r o   t  ator

• L[i, j]: length of longest palindromic subsequence in string xs[i:j] where i<=j.

def L(i, j): # closed interval
  if i > j: return 0 # no letters
  if i == j: return 1 # single letter palindrome
  if x[i] == x[j]: 
    return 2 + l(i+1, j-1)
  return max(L(i+1, j), L(i, j-1))

• number of subpbroblems: $O(n^2)$. Time per subproblem assuming recursion is free: $O(1)$. Hence, total time is $O(n^2)$.

Optimal binary search trees

Find most balanced BST for a set of keys. We have weights for the keys, which are search probabilities. Find a BST T (there are exponential number of BSTs) that minimizes $\sum_i w_i (depth_T(k_i) + 1)$. Depth of root is 0. Depth of a node is distance from the root. This minimizes expected search cost.

Enumeration

We have exponentially many trees.

Greedy soltution / Why doesn't greedy work?

Assume the keys are sorted. Pick K[i] in some greedy fashion (max.weight). This immediately splits the set of keys into the left and right. If we define e(i, j) to be the cost of the optimal BST on keys k[i], ..., k[j] .

greedy:
-------
        2|w=10
1|w=1           4|w=9
           3|w=8

optimal:
-------
         3|w=8
    2|w=10    4|w=9
1|w=1         

DP

• Guess all possible root nodes. The greedy algorithm doesn't try to guess the root node, that's the only difference.

-- e(i, j): cost of tree with keys k: i <= k <= j
def e(i, j):
  if i == j: return w[i]
  # | WRONG
  return min([e(i, r-1) + e(r+1, j) + w[r] 
              for k in range(i, j+1)])

The weights are going to change when we increase depth, so we actually need to add all the weights from i to j! So we write:

-- e(i, j): cost of tree with keys k: i <= k <= j
def e(i, j):
  if i == j: return w[i]
  # | WRONG
  return min([e(i, r-1) + e(r+1, j) + weight(i, j)
                 for k in range(i, j+1)])

Alternating coins

Have a list of coins. We have an even number of coins. Can only pick coins from the outside.

First player can always not lose in the game. What the first player does is compute v[1] + v[3] + ... v[n-1] versus v[2] + v[4] + ... which is even. If the odd values win, the he picks v[1]. P2 can pick v[2] or v[n]. P1 can pick either v[3] or v[n-1] depending on if P2 picked v[2] or v[n].

• We now want to maximize the amount of money.

v(i, j) = max([ range is(i+1, j) with P2 + v[i],
                range is (i, j-1) with P2 + v[j] ])

If we have v(i+1, j) subproblem with the opponent picking, we are guaranteed that the opponent plays min(v(i+1, j-1), v(i+2, j)). So we can unfold this, to get the full DP:

v(i, j) = max([  min(v(i+1, j-1), v(i+2, j)) + v[i],
                  min(v(i, j-1), v(i+1, j)) + v[j],

DP: All pairs shortest paths.

Accuracy vs precision

I had a hard time remembering which is which, so here's how I do it now. First, I think of it from a probabilistic lens, where one of them is the mean, and the other is variance of a gaussian distribution as shown above. We don't yet know whether accuracy is the mean or the variance.

Next, recall that it's linguistically correct to say:

you're precisely wrong

but not

you're accurately wrong.

Thus, we can be precise about something wrong. That is, we can be very "precise" about "hitting the wrong target". So, precision ought not care about the true value, just about how well we hit something. This is exactly what the variance attempts to capture: how "spread out" we are, or "how well we hit the mean".

The accuracy itself is the distance between the mean of our distribution and the true reference value we want to hit.

Why is the gradient covariant?

• expanation of gradient being covariant in terms of the integral version

Politicization of science

• Reference

Multi ꙮ cular O: ꙮ / Eye of cthulu

• Multiocular O

You can't measure the one way speed of light

• Veritasium video

Show me the hand strategy

So, how do you surface covert-aggressions and covert-criticism? Enter the: Show Me The Hand Strategy The "show me the hand strategy" can be applied with several techniques, including: Pretend you don't understand: if you don't understand and they did want to make their point across, they will be forced to be more direct in their aggression / offense Ask them what exactly do they mean: you can use the broken record technique here, where you keep repeating "what do you mean by that", "OK, but it does sound like you were trying to criticize my work. It's OK if you do", "then, if you didn't want to criticize, what did you mean" Go meta: explain them what they were doing, and tell them that you prefer direct talk because "you can take it" (invite criticism into the open), because you "expect better from them" (big judge power move), or because "it's so much better for both" (leader-like win-win approach) Reframe their aggression as support: nice power move and you will possibly get under their skin when they wanted to get under yours. They wanted to hurt you, or to harm your status, so when you reframe their attack as support, they will feel compelled to come out in the open and be more direct

Words that can be distinguished from letters if we know the sign of the permutation

#!/usr/bin/env python3
with open("google-10000-english.txt", "r") as f:
    words = [w.strip() for w in f.readlines()]


sorted = {}
for w in words:
    wsort = list(w)
    wsort.sort()
    wsort = "".join(wsort)
    if wsort in sorted:
        sorted[wsort].append(w)
    else:
        sorted[wsort] = [w]

collisions = 0
for wk in sorted:
    if len(sorted[wk]) == 1: continue
    collisions += 1
    print(sorted[wk])
    print("---")

print(collisions, len(words), 100.0 * float(collisions) / len(words))


collisions = 0
for wk in sorted:
    collidews = sorted[wk]
    for i in range(len(collidews):
            for j in range(i+1, len(collidews))
    collisions += 1
    print(sorted[wk])
    print("---")

Easy times don't create weak people, they just allow weak people to survive.

Easy times doesn't weaken the generator side of things, it simply weakens the adverserial side of things allowing weak people to survive.

Multiplicative weights algorithm (TODO)

How to fairly compare groups

Why is this a key argument? It’s really quite simple. Let’s say I have two groups, A and B. Group A has 10 people, group B has 2. Each of the 12 people gets randomly assigned a number between 1 and 100 (with replacement). Then I use the highest number in Group A as the score for Group A and the highest number in Group B as the score for Group B. On average, Group A will score 91.4 and Group B 67.2. The only difference between Groups A and B is the number of people. The larger group has more shots at a high score, so will on average get a higher score. The fair way to compare these unequally sized groups is by comparing their means (averages), not their top values. Of course, in this example, that would be 50 for both groups – no difference!

• Chessbase article about men v/s women in chess

Z algorithm (TODO)

The Z algorithm, for a given string $s$, computes a function $Z: [len(s)] \rightarrow [len(s)]$. $Z[i]$ is the length of the longest common prefix between $S$ and $S[i:]$. So, $S[0] = S[i]$, $S[1] = S[i+1]$, $S[2] = S[i+2]$, and so on till $S[Z[i]] = S[i + Z[i]]$, and then $S[Z[i]+1] \neq S[i + Z[i] + 1]$.

If we can compute the Z function for a string, we can then check if pattern P is a substring of text T by constructing the string P#T$. Then, if we have an index such that Z[i] = len(P), we know that at that index, we have the string P as a substring.

Note that the Z-algorithm computes the Z function in linear time.

const int N = 1000;
int z[N];
char s[N] = "hello, world";
int n;

// write the z array into the array z for the string s
void mkz(const char *s, int *z) {
    const int N = strlen(s);
    int curi = 0;
    while(s[curi]) {
        int matchlen = 0; 
        while(curi + matchlen < N) {
            if (s[curi + matchlen] == s[matchlen]) { matchlen++; }
            else { break; }
        }
        z[curi] = matchlen;

        for(int i = 0; i < matchlen && i < curi; ++i) { z[curi + i] = z[i]; }
        curi += matchlen;
    }
}

int main() {
in
}

• Reference: Algorithms on strings, trees, and sequences.

Bijection from (0, 1) to [0, 1]

Rene Girard

• Link where I first heard of him

Noam Chomsky on anarchism (WIP)

• Video of interview
• Emma Goldman Archives

Interview

What do we do with people who don't want to work or those with crimimal tendencies? What do we do with people's interests, do they deserve to interchange jobs?

There would a general agreement between people who call themselves anarchists should maximise people's abilities to fulfil their potential.

Another problem is that at any point in human history, people have not understood what is opression. Chomsky's grandmother didn't think she was opressed while being in a patriarchial family.

What is anarchism

• What is anarchism

Start with Rudolf Rocker.

Anarchism is not a fixed social system with fixed answers, but a trend in mankind that drives for free unhindered unfolding

These derive from the Enlightenment. Thus institutions that constrain such development are illegitimate unless they can justify themselves. Adam Smith extolls the wonder of division of labour. Deeper into the book, he argues that in any civilized society, the government must not allow division of labour for it makes a human as stupid as they can be.

Anarchism seeks to identify structures of domination, authority, etc that constrain human development. It then challenges them to justify themselves. If you cannot meet the challenge, the structure should be dismantled and reconstructed from below.

Anarchism is basically 'truism', which has the merit, at least, of being true. It's an interesting category of principles that are universal and doubly universal: universally accepted, and universally rejected in practice!

Slavoj Zizek: Violence

• Video talk at google

What does violence react to? What is the everyday texture of our lives? Ideology in the sense of complicated networks of social, political prejudices determines the way we functions and structures our life. What is ideology?

Donald Rumsfield, gulf war, spoke about known knows (saddam is a dictator), known unknowns ('WMD that saddam surely had'), and unknown unknowns ('even worse WMD that saddam may have').

What about unknown knowns? Things we don't know that we know? This is ideology. The texture into which we are embedded.

European trinity: France (revolutionary, political), German (conservative, poets, thinkers), Anglo saxon (liberal, economy).

Bohr had a horsheshoe above his house. 'Do you believe in it? Aren't you a scientist?' 'Of course I don't believe in it! But I was told that it works regardless of my belief in it!'.

What is ideology today? It seems very shallow, things of the form 'go achieve', and whatnot. However, there is a lot more that is tacit.

'Interpassivity': we transpose onto the other our passive reaction. Others are passive for us. Canned laughter on TV. Literally, the TV set laughs for you. You feel relief as if you have laughed.

Similarly it's not that we believe. We need someone else to believe for us. For example, santa Claus. The parent's don't believe, they do it to not let down the kids. The kids don't believe, they pretend for presents and to not let down the parents. The whole system of belief functions.

The first person to do this politically is the isareli prime minister Golda Meir. When asked 'do you believe in god'. Her answer was 'no. I believe in jewish people, and they believe in God'. But atheism is ~70% of israel.

When different cultures are thrown together (globalism) we should break the spell of liberalism: we cannot understand each other, we don't even understand ourselves. I don't want to understand all cultures. We need a code of discretion. How do we sincerely politely ignore each other? We need proper distance to treat others in a non-racist, kind manner.

He upholds that we don't even miss anything deep in this way. Do I really understand you? Do I really understand myself?

We are the stories we are telling ourselves about ourselves. The basic freedom is to tell your side of the story.

The motto of tolerance:

An enemy is someone whose story I have not yet heard.

Living libraries, people can visit minorities and talk to them. It works at a certain level. But it stops working at some level. Because we would not say the same of Hitler. 'The X files insight'. Truth is out there. It's not in what you are telling yourself about yourself. The story you are telling yourself is a lie.

Two extreme examples. One from Europe, one from far east.

• Grey Eminence
• Zen at War

Corruption is prohibited officially, and it is exactly codified in a communist country. Holidays in Japan. You are given 40 days. It's very impolite to take more than 20 days. This creates a link between people, the link of politeness. This is ideology. Prohibition is is prohibited to be stated publicly.

Nazi germany without glasses is 'sacrifice your country'. With glasses, it is 'do this, pretend to do this, we can have some fun, beat the jews'. Ideology always offers you some bribery.

When hitler finishes giving a talk, the people clap. In a communist speech, at the end of the speech, the speaker claps with the people. This is a crystallization of the difference between fascism and communism.

'Nice to meet you, how are you?' is a sincere lie. From the very beginning we entered into language, we enter into requiring one for whom we can create appearances.

• Zizek interview at BBC

The light at the end of the tunnel is an oncoming train

Embracing hopelessness means to accept that there are no easy solutions. We should accept the hopelessness and start a paradigm shift. Our tragedy is death. Something will have to change fundamentally. We do not yet have the formula of what to do. We can now only get ready for a global crisis.

The problem with Hitler was that he wasn't violent enough. In the same way that Gandhi was more violent than Hitler, in terms of 'systemic change'. Hitler killed millions to save the system. Gandhi killed no one to setup a radical change. Change will hurt.

We tend to forget the violence of keeping things the same, and we only consider the violence of change. Sometimes the gratest violence is to not participate.

Modi, China, Russia: Global market, Cultural narrowness.

Polyamory is instrumental. True love is where you cannot be without someone else.

It is a sign of progress that some things are considered ideology. For example, ''is it right to kill?'' will be laughed at. The problem with current societies is that we are eroding the set of things we can laugh at due to dangerous ideas of relativism.

• Zizek v/s Petersen

Petersen: truths of the communist manifesto:

• History is to be viewed as an economic class struggle.
• Hierarchical structure is not attributable to capitalism.
• We're also in odds with nature, which never shows up in Marx.
• Hierarchical structures are necessary to solve complicated problems.
• Human hierarchy is not based on power. Power is a very unstable means of exploiting people.
• History comes off as a 'binary' class struggle in Marx.
• 'Dictatorship of the proleteriat': Race to bottom of wages. The fact that we assume that all the evil could be attributed to the bourgouise itself setup the seeds for revolution.
• How will the replacement of the bourgouise happen? Why wouldn't the proleteriat become as or more corrupt than the capitalists?
• What makes you believe that you can take a complicated system like the free market and then centralize this?
• A capitalist who is running a business as a manager does add value.
• The criticism of profit. What's wrong with profit? Profit is theft is the marxist principle. If the capitalist adds value to the corporation, then they do deserve profit. Profit sets a constraint on wasted labour. There are forms of stupidity you cannot engage in because the market will punish you for it.
• 'The dictatorship of the proleteriat' would become hyper-productive. How? The theory seems to be that once we eradicate the profit motive and the bourgouise allows them to become hyper productive.
• We need hyper productivity for the dictatorship of the proleteriat to create enough goods for everyone. When this happens, everyone will engage in meaningful creative labour, which they had been alienated from in capitalism. Then this will create a utopia.
• Does this utopia really be the right utopia for everyone?
• The Dostovyeskian observation: what shallow take on people do you need to believe that if you hand people everything they need, they'll be happy? We were built for trouble. Hanging out on the beach is a vacation, not a job. We would destroy things just so something can happen just so we can have the adventure of our lives.
• Marx and Engels admit that there has not been a system that's capable to produce materials in excess as capitalism.

Zizek:

• The irony of how Petersen and him are both marginalized by the academic community.
• China today: strong authoritarian state, wild capitalist dynamics. It's managed to uplift hundreds of millions of people out of poverty. They want the Cofuscian ideal of harmonious society.
• Happiness as goal of life is problematic. Humans are creative in sabotaging pursuit of happiness. We have to find a meaningful cause beyond the mere struggle for pleasurable survival. Modernity means that we should carry the burden of freedom of choice.
• Never presume that your sufferring is in itself a proof of authenticity. Renunciation of pleasure can turn into the pleasure of renunciation.

Poverty: Who's to blame?

• Video

First blame countries

• Third world countries have terrible economic policies
• Administrations in third world countries are dysfunctional.
• First world countries block workers from immigrating for which we can blame first world countries.

Secondly blame individuals: The trifecta

• work at a stable job even if the job is not fun
• don't have kids if you can't afford it

Blame matters

• Blame affects wheher something is a social issue. For example, is the opioid epidemid a social behaviour? or should we just blame individuals?
• Blame affects who should be shamed for failing to change their behaviour.

Books to read

• Doing the best I can
• Promises I can keep

Learn Zig in Y minutes

• imports:

const std = @import("std");

• globals:

// global variables.
const x = 1234;

• comments:

//! Top level comments are setup using //!
//! This module provides functions for retrieving the current date and
//! time with varying degrees of precision and accuracy. It does not
//! depend on libc, but will use functions from it if available.

• main:

pub fn main() !void {
    const stdout = std.io.getStdOut().writer();
    try stdout.print("Hello, {}!\n", .{"world"});
    // Comments in Zig start with "//" and end at the next LF byte (end of line).
    // The below line is a comment, and won't be executed.

• ints:

    // integers
    const one_plus_one: i32 = 1 + 1;
    print("1 + 1 = {}\n", .{one_plus_one});

• floats:

    // floats
    const seven_div_three: f32 = 7.0 / 3.0;
    print("7.0 / 3.0 = {}\n", .{seven_div_three});

• bools:

    // boolean
    print("{}\n{}\n{}\n", .{
        true and false,
        true or false,
        !true,
    });

• optionals:

    // optional
    var optional_value: ?[]const u8 = null;
    assert(optional_value == null);

    print("\noptional 1\ntype: {}\nvalue: {}\n", .{
        @typeName(@TypeOf(optional_value)),
        optional_value,
    });

    optional_value = "hi";
    assert(optional_value != null);

    print("\noptional 2\ntype: {}\nvalue: {}\n", .{
        @typeName(@TypeOf(optional_value)),
        optional_value,
    });

• errors:

    // error union
    var number_or_error: anyerror!i32 = error.ArgNotFound;
    print("\nerror union 1\ntype: {}\nvalue: {}\n", .{
        @typeName(@TypeOf(number_or_error)),
        number_or_error,
    });
    number_or_error = 1234;
    print("\nerror union 2\ntype: {}\nvalue: {}\n", .{
        @typeName(@TypeOf(number_or_error)),
        number_or_error,
    });
    // It works at global scope as well as inside functions.
    const y = 5678;
}

• Top level ordering:

// Top-level declarations are order-independent:
pub fn g() { f(); }
pub fn f() {}

• strings:

test "string literals" {
    const bytes = "hello";
    assert(@TypeOf(bytes) == *const [5:0]u8);
    assert(bytes.len == 5);
    assert(bytes[1] == 'e');
    assert(bytes[5] == 0);
    assert('e' == '\x65');
    assert('\u{1f4a9}' == 128169);
    assert('💯' == 128175);
    assert(mem.eql(u8, "hello", "h\x65llo"));
}

The algebraic structure of the 'nearest smaller number' question

The nearest smaller number problem can be solved by using a stack along with an observation of monotonicity. This is explained in the USACO guide to stacks in the Gold section.

What I find interesting is that we need a stack. Why does a stack show up? Stacks are usually related to a DFS on some appropriate object. What's that object? And can we gain insight into when we need to use a stack based on this?

The idea is that we are trying to construct the Hasse diagram of the original array, treated as a poset with ground set $P \equiv { (val, ix) : \texttt{arr}[ix] = val }$ with the ordering $(a_1, a_2) < (b_1, b_2) \iff a_1 < b_1 \land a_2 < b_2$.

So we have this hasse diagram, which interestingly is going to be a tree. this need not always be the case! consider the divisiblity poset with the elements $3, 5, 15$.

Then the answer is to print the parent of each node in the tree as the parent in the Hasse diagram is going to be closest number that is smaller than it.

Why does this Hasse diagram show up? What is the relationship between this problem, and that of Graham Scan which also uses a similar technique of maintaining a stack. Does this also have a hasse diagram associated to it? or a DFS tree?

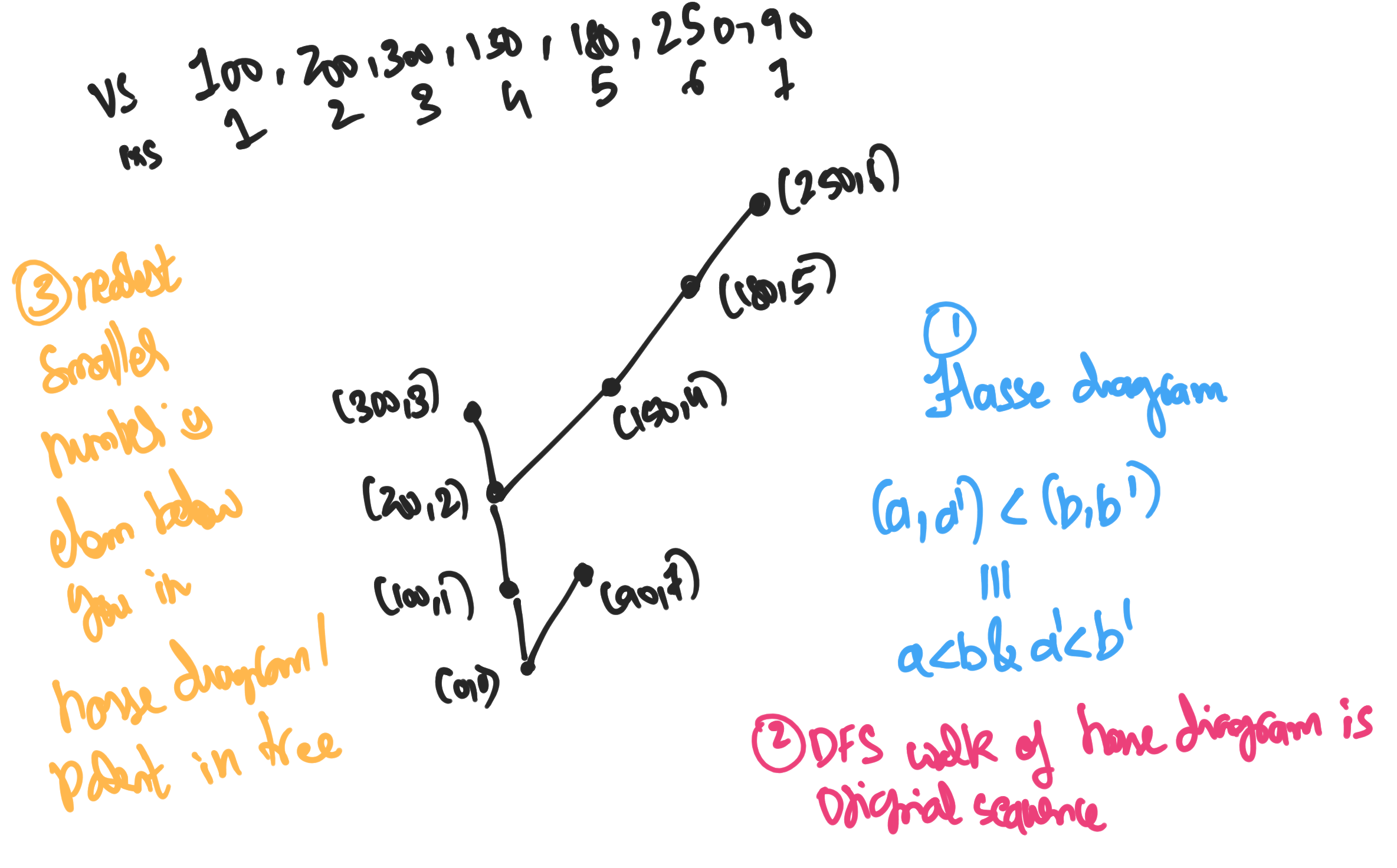
Why loss of information is terrifying: Checking that a context-free language is regular is undecidable

This comes from applying Greibach's theorem. I find myself thinking about this theorem once in a while, and its repercussions. If we once had access to God who tabulated for all all regular languages described as context free grammars, and we lost this tablet, we're screwed. There's no way to recover this information decidably.

It shows that moving to higher models of computation (From regular to context free) can sometimes be irreversably damaging.

Sciences of the artificial

A bridge under its usual conditions of service, behaves simply as a relatively smooth level surface. Only when it has been overloaded do we learn the physical properties of the materials from which it is built.

Ohm's law was suggested to its discovered by its analogy with some simple hydraulic phenomena.

Why simulation is useful:

• 1. (obvious): while the axioms maybe obvious, their raminifactions may not.

A NASA launched satellite is surely an artificial object, but we usually do not think of it as simulating the moon; It simply obeys the same laws.

• 2. (subtle) Each layer only depends on an abstraction of the previous. Airplanes don't need the correctness of the Eightfold Way.

Babbage introduced the words "Mill" and "Store"

The focal concern of Economics is allocation of scarce resources.

We can use a theory (say a theory of profit-loss) either positively, as an explaiation, or normatively, as a way to guide how we should run a firm.

Numbering nodes in a tree

If we consider a tree such as:

      a
b         c
        d   e

The "standard way" of numbering, by starting with a 0 and then appending a 0 on going to the left, appending a 1 on going to the right doesn't make a great deal of sense. On the other hand, we can choose to number them as follows:

• Consider the root to have value 1
• Every time we go right, we add 1/2^{height}. When we go left, we subtract 1/2^{height}.
• This gives us the numbers:

      1
0.5       1.5
       1.25     1.75

• This also makes intuitive why to find the node to replace 1.5 when we delete it is to go to the left child 1.25 and then travel as much to the right as possible. That path corresponds to:

$$ \begin{aligned} &1 + 1/2 - 1/4 + 1/8 + 1/16 + \dots \ &= 1 + 1/2 - 1/4 + 1/4 \ &= 1.5 \end{aligned} $$

• So in the limit, the rightmost leaf of the left child of the parent has the same value as the parent itself. In the non-limit, we get as close as possible.

• This also may help intuit hyperbolic space? Distances as we go down in the three shrink. Thus, it's easier to "escape" away to the fringes of the space, rather than retrace your step. Recall that random walks in hyperbolic space almost surely move away from the point of origin. It feels to me like this explains why. If going towards the root / decreasing heighttakes distance $d$, going deeper into the tree / increasing the height needs distance $d/2$. So a particle would "tend to" travel the shorter distance.

Number of vertices in a rooted tree

Make sure the edges of the tree are ordered to point away from the root $r$. So, for all edges $(u, v) \in E$, make sure that $d(r, v) = d(r, u) + 1$.

Create a function $terminal$ which maps every outward arc to its target. $terminal: E \rightarrow V$, $terminal((u, v)) = v$.

This map gives us an almost bijection from edges to all vertices other than the root. So we have that $|E| + 1 = |V|$. Each of the edges cover one non-root vertex, and we then $+1$ to count the root node.

I found this much more intuitive than the inductive argument. I feel like I should attempt to "parallelize" inductive arguments so you can see the entire counting "at once".

Median minimizes L1 norm

Consider the meadian of $xs[1..N]$. We want to show that the median minimizes the L1 norm $L_1(y) = \sum_i |xs[i] - y|$. If we differentiate $L_1(y)$ with respect to $y$, we get:

$$ d L_1(y)/y = \sum_i - \texttt{sign}(xs[i] - y) $$

Recall that $d(|x|)/dx = \texttt{sign}(x)$

Hence, the best $y$ to minimize the $L_1$ norm is the value that makes the sum of the signs $\sum_i \texttt{sign}(xs[i] - y)$ minimal. The median is perfect for this optimization problem.

1. When the list has an odd number of elements, say, $2k + 1$, $k$ elements will have sign $-1$, the middle element will have sign $0$, and the $k$ elements after will have sign $+1$. The sum will be $0$ since half of the $-1$ and the $+1$ cancel each other out.
2. Similar things happen for even, except that we can get a best total sign distance of $+1$ using either of the middle elements.

Proof 2:

Math.se has a nice picture proof abot walking from left to right.

Proof 3:

Consider the case where $xs$ has only two elements, with $xs[0] < xs[1]$. Then the objective function to minimize the L1 norm, ie, to minimize $|xs[1] - y| + |xs[2] - y|$. This is satisfied by any point in between $xs[1]$ and $xs[2]$.

In the general case, assume that $xs[1] < xs[2] \dots < xs[N]$. Pick the smallest number $xs[1]$ and the largest number $xs[N]$. We have that any $y$ between $xs[1]$ and $xs[N]$ satisfies the condition. Now, drop off $xs[1]$ and $xs[N]$, knowing that we must have $y \in [xs[1], xs[N]]$. Recurse.

At the end, we maybe left with a single element $xs[k]$. In such a case, we need to minimize $|xs[k] - y|$. That is, we set $xs[k] = y$.

On the other hand, we maybe left with two elements. In this case, any point between the two elements is a legal element.

We may think of this process as gradually "trapping" the median between the extremes, using the fact that that any point $y \in [l, r]$ minimizes $|y - l| + |y - r|$!

• Taken from math.se

LISP quine

I learnt how to synthesize a LISP quine using MiniKanren. It's quite magical, I don't understand it yet.

((lambda (x)            
   `(,x (quote ,x)))    
 (quote                 
   (lambda (x)          
     `(,x (quote ,x)))))

A slew of order theoretic and graph theoretic results

I've been trying to abstract out the activity selection problem from the lens of order theory. For this, I plan on studying the following theorems/algebraic structures:

• Intransitive indifference with unequal indifference intervals
• Mirsky's theorem
• Dilworth's theorem
• Gallai–Hasse–Roy–Vitaver theorem
• Dirac's theorem
• Ore's theorem
• Course on discrete math
• cs.stackexchange: Finding longest chain in poset in sub-quadratic time

Naively, the solution goes as follows, which can be tested against CSES' movie festival question

// https://cses.fi/problemset/task/1629
int main() {
    int n;
    cin >> n;
    vector<pair<int, int>> ms(n);
    for (int i = 0; i < n; ++i) {
        cin >> ms[i].first >> ms[i].second;
    }

    std::sort(ms.begin(), ms.end(), [](pair<int, int> p1, pair<int, int> p2) {
        return (p1.second < p2.second) ||
               (p1.second == p2.second && p1.first < p2.first);
    });

    int njobs = 0;
    int cur_end = -1;
    for (int i = 0; i < n; ++i) {
        if (cur_end <= ms[i].first) {
            cur_end = ms[i].second;
            njobs++;
        }
    }
    cout << njobs << "\n";
    return 0;
}

Explanation 1: exchange argument

• The idea is to pick jobs greedily, based on quickest finishing time.
• The argument of optimality is strategy stealing. Think of the first job in our ordering O versus the optimal ordering O*.
• If we both use the same job, ie, O[1] = O*[1], recurse into the second job.
• If we use different jobs then O[1] != O*[1].
• Since O[1] ends quickest [acc to our algorithm], we will have that end(O[1]) < end(all other jobs), hence end(O[1]) < end(O*[1]).
• Since O* is a correct job schedule, we have that end(O*[1]) < start(O*[2]).
• Chaining inequalities, we get that end(O[1]) < end(O*[1]) < start(O*[2]).
• Thus, we can create O~ which has O~[1] = O[1] and O~[rest] = O*[rest]. (~ for "modified").
• Now recurse into O~ to continue aligning O* with O. We continue to have the same length between O~, O and O*.

Explanation 2: posets and interval orders

Thebes

• BBC in our time

Beethoven

• BBC in our time

Neko to follow your cursor around

$ oneko -idle 0 -speed 100 -time 5120 -bg blue -fg orange -position +20+20

This is useful for screen sharing tools that can't display the mouse pointer, like Microsoft Teams

Non commuting observables: Light polarization

• physics.se

Statement expressions and other GCC C extensions

This seems really handy. I've always loved that I could write

let x = if y == 0 { 1 } else { 42}

in Rust. It's awesome to know that the C equivalent is

const int x =  ({ if (y == 0) { return 1; } else { return 42; });

Conditions (?:) with omitted operands

x ?: y =defn= x ? x : y

variable length arrays

FILE *
concat_fopen (char *s1, char *s2, char *mode)
{
  char str[strlen (s1) + strlen (s2) + 1];
  strcpy (str, s1);
  strcat (str, s2);
  return fopen (str, mode);
  // str is freed here.                                
}

Designated array initializers: A better way to initialize arrays

• initialize specific indexes

// initialize specific indexes
int a[6] = { [4] = 29, [2] = 15 };
// a[4] = 29; a[2] = 15; a[rest] = 0

• initialize ranges:

// initialize ranges
int widths[] = { [0 ... 9] = 1, [10 ... 99] = 2, [100] = 3 };

• initialize struct fields:

//initialize struct fields
struct point { int x, y; };
struct point p = { .y = yvalue, .x = xvalue };

• initialize union variant:

//initialize union variant
union foo { int i; double d; };
union foo f = { .d = 4 };

• Neat trick: lookup for whitespace in ASCII:

int whitespace[256]
  = { [' '] = 1, ['\t'] = 1, ['\h'] = 1,
      ['\f'] = 1, ['\n'] = 1, ['\r'] = 1 };

Cast to union

union foo { int i; double d; };
int x = 42; z = (union foo) x;
double y = 1.0; z = (union foo) y;

Dollar signs in identifier names

int x$;
int $z;

Unnamed union fields

struct {
  int a;
  union { int b; float c; };
  int d;
} foo

// foo.b has type int
// foo.c has type float, occupies same storage as `foo.b`.

• GCC manual: statement expressions
• GCC manual: C extensions

A quick look at impredicativity

I found this video very helpful, since I was indeed confused about the two meanings of impredicativity that I had seen floating around. One used by haskellers, which was that you can't instantiate a type variable a with a (forall t). Impredicative in Coq means having (Type : Type).

• polymorphic types:

forall p. [p] -> [p] -- LEGAL
Int -> (forall p. [p] -> [p])  -- ILLEGAL
(forall p. [p] -> [p])  -> Int -- ILLEGAL
[forall a. a -> a] -- ILLEGAL

• Higher rank types: forall at the outermost level of a let-bound function, and to the left and right of arrows!

Int -> (forall p. [p] -> [p])  -- LEGAL
(forall p. [p] -> [p])  -> Int -- LEGAL
runST :: (forall s. ST s a) -> a -- LEGAL
[forall a. a -> a] -- ILLEGAL

• Impredicative type:

[forall a. a -> a]

• We can't type runST because of impredicativity:

($) :: forall a, forall b, (a -> b) -> a -> b
runST :: forall a, (forall s, ST s a) -> a -- LEGAL
st :: forall s. ST s Int
runST st -- YES
runST $ st -- NO 

• Expanding out the example:

($) runST st
($) @ (forall s. ST s Int) @Int  (runST @ Int) st

• Data structures of higher kinded things. For example. we might want to have [∀ a, a -> a]
• We have ids :: [∀ a, a -> a]. I also have the function id :: ∀ a, a -> a. I want to build ids' = (:) id ids. That is, I want to cons an id onto my list ids.
• How do we type infer this?

How does ordinary type inference work?

reverse :: ∀ a. [a] -> [a]
and :: [Bool] -> Bool
foo = \xs -> (reverse xs, and xs)

• Start with xs :: α where α is a type variable.
• Typecheck reverse xs. We need to instantiate reverse. With what type? that's what we need to figure out!
• (1) Instantiate: Use variable β. So we have that our occurence of reverse has type reverse :: [β] -> [β].
• (2) Constrain: We know that xs :: α and reverse expects an input argument of type [β], so we set α ~ [β] due to the call reverse xs.
• We now need to do and xs. (1) and doesn't have any type variables, so we don't need to perform instantiation. (2) We can constrain the type, because and :: [Bool] -> Bool, we can infer from and xs that α ~ [Bool]
• We solve using Robinson unification. We get [β] ~ α ~ [Bool] or β = Bool

Where does this fail for polytypes?

• The above works because α and Β only stand for monotypes.
• Our constraints are equality constraints, which can be solved by Robinson unification
• And we have only one solution (principal solution)
• When trying to instantiate reverse, how do we instantiate it?
• Constraints become subsumption constraints
• Solving is harder
• No principal solution
• TODO: construct an example for this intuition? I don't understand it.
• Consider incs :: [Int -> Int], and (:) id incs versus (:) id ids.

But it looks so easy!

• We want to infer (:) id ids
• We know that the second argument ids had type [∀ a, a -> a]
• we need a type [p] for the second argument, because (:) :: p -> [p] -> [p]
• Thus we must have p ~ (∀ a, a -> a)
• We got this information from the second argument
• So let's try to treat an application (f e1 e2 ... en) as a whole.

New plan

• Assume we want to figure out filter g ids.
• start with filter :: ∀ p, (p -> Bool) -> [p] -> Bool
• Instatiate filter with instantiation variables κ to get (κ -> Bool) -> [κ] -> Bool
• Take a "quick look" at e1, e2 to see if we know that κ should be
• We get from filter g ids that κ := (∀ a, a -> a).
• Substitute for κ (1) the type that "quick look" learnt, if any, and (2) A monomorphic unification variable otherwise.
• Typecheck against the type. In this case, we learnt that κ := (∀ a, a -> a), so we replace κ with (∀ a, a -> a).
• Note that this happens at each call site!

The big picture

Replace the idea of:

• instantate function with unficiation variables, with the idea.
• instantiate function with a quick look at the calling context.
• We don't need fully saturated calls. We take a look at whatever we can see!
• Everything else is completely unchanged.

What can QuickLook learn?

• Video

Data oriented programming in C++

• Calcuating entropy to find out if a variable is worth it! Fucking amazing.
• Video

Retro glitch

• There's something great about the juxtaposition of the classic Christian scene with the glitch aesthetic. I'm unable to articulate what it is that I so thoroughly enjoy about this image.

• Fuck me, it turns out this is fascist art, goes by the genre of fashwave. Pretty much everything else in this genre is trash, this is the sole 'cool looking' picture of the lot.

SSA as linear typed language

• Control flow is linear in a basic block: ie, we can have a sea of nodes representation, where each terminator instruction produces linear control flow tokens: br: token[-1] --> token[1]. brcond: token[-1] -> -> (token[1], token[1]), return: token[-1] -> (). This ensures that each branching only happens once, thereby "sealing their fate. On the other hand, reguar instructions also take a "control token", but don't consume it. so for example, add: token[0] -> (name, name) -> name.

• Next question: is dominance also somehow 'linear'?

• Answer: yes. We need quantitative types. When we branch from basic block A into blocks B, C attach 1/2A to the control tokens from (%tokb, %tokc) = br cond %cond0 B, C. Now, if someone builds a token that's at a basic block D that is merged into by both B, C, they will receive a "full" A that they can use. Pictorially:

       A
       ...

   B        C  
[1/2A]     [1/2A]
       D
       1A

Nix weirdness on small machines

[email protected]:~$ nix-env -iA nixpkgs.hello                                                                                    
+ nix-env -iA nixpkgs.hello                                                                                                          
installing 'hello-2.10'                                                                                                              
these paths will be fetched (0.04 MiB download, 0.20 MiB unpacked):                                                                  
  /nix/store/w9yy7v61ipb5rx6i35zq1mvc2iqfmps1-hello-2.10                                                                             
copying path '/nix/store/w9yy7v61ipb5rx6i35zq1mvc2iqfmps1-hello-2.10' from 'https://cache.nixos.org'...                              
error: unable to fork: Cannot allocate memory                                                                                        
[email protected]:~$ gdb --args nix-env -iA nixpkgs.hello                                                                         
+ gdb --args nix-env -iA nixpkgs.hello                                                                                               
GNU gdb (Ubuntu 7.11.1-0ubuntu1~16.5) 7.11.1                                                                                         
Copyright (C) 2016 Free Software Foundation, Inc.                                                                                    
License GPLv3+: GNU GPL version 3 or later <http://gnu.org/licenses/gpl.html>                                                        
This is free software: you are free to change and redistribute it.                                                                   
There is NO WARRANTY, to the extent permitted by law.  Type "show copying"                                                           
and "show warranty" for details.                                                                                                     
This GDB was configured as "x86_64-linux-gnu".                                                                                       
Type "show configuration" for configuration details.                                                                                 
For bug reporting instructions, please see:                                                                                          
<http://www.gnu.org/software/gdb/bugs/>.                                                                                             
Find the GDB manual and other documentation resources online at:                                                                     
<http://www.gnu.org/software/gdb/documentation/>.                                                                                    
For help, type "help".                                                                                                               
Type "apropos word" to search for commands related to "word"...                                                                      
Reading symbols from nix-env...(no debugging symbols found)...done.                                                                  
(gdb) run                                                                                                                            
Starting program: /nix/store/d6axkgf0jq41jb537fnsg44080c4rd52-user-environment/bin/nix-env -iA nixpkgs.hello                         
warning: File "/nix/store/danv012gh0aakh8xnk2b35vahklz72mk-gcc-9.2.0-lib/lib/libstdc++.so.6.0.27-gdb.py" auto-loading has been declin
ed by your `auto-load safe-path' set to "$debugdir:$datadir/auto-load".                                                              
To enable execution of this file add                                                                                                 
        add-auto-load-safe-path /nix/store/danv012gh0aakh8xnk2b35vahklz72mk-gcc-9.2.0-lib/lib/libstdc++.so.6.0.27-gdb.py             
line to your configuration file "/home/floobits/.gdbinit".                                                                           
To completely disable this security protection add                                                                                   
        set auto-load safe-path /                                                                                                    
line to your configuration file "/home/floobits/.gdbinit".                                                                           
For more information about this security protection see the                                                                          
"Auto-loading safe path" section in the GDB manual.  E.g., run from the shell:                                                       
        info "(gdb)Auto-loading safe path"                                                                                           
warning: File "/nix/store/xg6ilb9g9zhi2zg1dpi4zcp288rhnvns-glibc-2.30/lib/libthread_db-1.0.so" auto-loading has been declined by your
 `auto-load safe-path' set to "$debugdir:$datadir/auto-load".                                                                        
warning: Unable to find libthread_db matching inferior's thread library, thread debugging will not be available.                     
^[[A[New LWP 21466]                                                                                                                  
GC Warning: Failed to expand heap by 128045056 bytes                                                                                 
installing 'hello-2.10'                                                                                                              
building '/nix/store/k3kz3cwyqdwi5bmwcbl1fzv2b2wkqrl6-user-environment.drv'...                                                       
created 43 symlinks in user environment                                                                                              
[LWP 21466 exited]                                                                                                                   
[Inferior 1 (process 21462) exited normally]                                                                                         
(gdb) run                                                                                                                            

All nix subcommands are just symlinks

[email protected]:~/idfk/nix-master$ ls -al /nix/store/4vz8sh9ngx34ivi0bw5hlycxdhvy5hvz-nix-2.3.7/bin/                            
total 1784                                                                                                                           
dr-xr-xr-x 2 floobits bollu    4096 Jan  1  1970 .                                                                                   
dr-xr-xr-x 9 floobits bollu    4096 Jan  1  1970 ..                                                                                  
-r-xr-xr-x 1 floobits bollu 1816768 Jan  1  1970 nix                                                                                 
lrwxrwxrwx 1 floobits bollu       3 Jan  1  1970 nix-build -> nix                                                                    
lrwxrwxrwx 1 floobits bollu       3 Jan  1  1970 nix-channel -> nix                                                                  
lrwxrwxrwx 1 floobits bollu       3 Jan  1  1970 nix-collect-garbage -> nix                                                          
lrwxrwxrwx 1 floobits bollu       3 Jan  1  1970 nix-copy-closure -> nix                                                             
lrwxrwxrwx 1 floobits bollu       3 Jan  1  1970 nix-daemon -> nix                                                                   
lrwxrwxrwx 1 floobits bollu       3 Jan  1  1970 nix-env -> nix                                                                      
lrwxrwxrwx 1 floobits bollu       3 Jan  1  1970 nix-hash -> nix                                                                     
lrwxrwxrwx 1 floobits bollu       3 Jan  1  1970 nix-instantiate -> nix                                                              
lrwxrwxrwx 1 floobits bollu       3 Jan  1  1970 nix-prefetch-url -> nix                                                             
lrwxrwxrwx 1 floobits bollu       3 Jan  1  1970 nix-shell -> nix                                                                    
lrwxrwxrwx 1 floobits bollu       3 Jan  1  1970 nix-store -> nix                                                                    

It seems the way this works is that the nix tool figures out from what symlink it's being invoked to decide what to do. God, that's ugly? brilliant? I don't even know.

How does writeFile work?

• cowsay in nixpkgs
• writeFile in nixpkgs
• runCommand' in nixpkgs
• mkDerivation in nixpkgs
• derivation in nixpkgs
• src/libexpr/primops/derivation.nix in nixos
• prim_derivationStrict in nixos c++
• derivationArg in nixos c++
• writeDerivation in nixos c++

Autodiff over derivative of integrals

• Reynolds transport theorem
• Physics based differential rendering

Proof of projective duality

In projective geometry, we can interchange any statement with "points" and "lines" and continue to get a true statement. For example, we have the dual statements:

• Two non-equal lines intersect in a unique point (including a point at infinty for a parallel line).
• Two non-equal points define a unique line.

The proof of the duality principle is simple. Recall that any point in projective geometry is of the from $[a : b : c] \simeq (b/a, c/a)$. A projective equation is of the form $px + qy + rz = 0$ for coefficients $p, q, r \in \mathbb C$.

• if we have a fixed point $[a : b : c]$, we can trade this to get a line $ax + by + cz = 0$.
• If we have a line $ax + by + cz = 0$, we can trade this to get a point $[a🅱️c]$.
• The reason we need projectivity is because this correspondence is only well defined upto scaling: the line $x + 2y + 3$ is the same as the line $2x + 3y + 6$.
• In using our dictionary, we would get $[1:2:3]$, $[2:4:6]$. Luckily for us, projectivity, these two points are the same! $(2/1, 3/1) = (4/2, 6/2)$.
• The "projective" condition allows us to set points and lines on equal footing: lines can be scaled, as can points in this setting.

Preventing the collapse of civilization

• video by Jonathan Blow
• The year civilization collapsed
• The thirty million line problem
• Civilizations: Institutions, Knowledge, and future
• Dark mountain

I am very sympathetic to the perspective that software has gotten far less reliable than it used to be.

Violent deaths in ancient societies (WIP)

Kanun in albania

Honor societies and Revence

Law codes: Code of Hammurabi

References

• Ethnographic and Archaeological Evidence on Violent Deaths
• Kanun

An elementary example of a thing that is not a vector

Consider the tripe (temperature, pressure, humidity) at a point. If we rotate the picture by 60 degrees, the triple does not change.

Now consider the direction of wind at a point. If we rotate the picture by 60 degrees, the components of the wind vector change with our rotation.

Thus:

a vector is something that transforms like a vector.

To be more precise, I can phrase it as:

A vector iss (is and only is) something that transforms like a vector.

Generalization to tensors is left as an exercise for the reader.

Elementary probability theory (WIP)

I've never learnt elementary probability theory "correctly". This is me attempting to fix it.

Defn: Sample space

set of all possible outcomes / things that could happen.

Defn: Outcome / Sample point / atomic event

An outcome consists of all the information about the experiment after it has been performed including the values of all random choices.

NOTE: Keeping straight event v/s outcome

It's easy to get confused between 'event' and 'outcome' (linguistically). I personally remember that one of them is the element of the sample space and another the subsets, but I can't remember which is which. Here's how I recall which is which:

every experiment has an outcome. We write an outcome section when we write a lab manual/lab record for a given experiment.

Now, we when perform an expriment, or something random happens, sometimes, the result (ie, the outcome) can be eventful; it's not linguistically right to say that some events can be outcomeful.

So, an event is a predicate over the set of outcomes; event: outcome -> bool. This is the same as being a subset of outcomes (the event is identified with the set of outcomes it considers eventful), so we have event ~= 2^outcomes.

Example: Monty hall

An outcome of the monty hall game when the the contestant switches consists of:

• the box with the prize.
• the box chosen by the contestant.
• the box that was revealed.

Once we know the three things, we know everything that happened.

For example, the sample point $(2, 1, 3)$:

• the prize is in box 2
• the player first picks box 1
• the assistant, Carol, reveals box 3.
• The contestant wins, because we're assuming the player switches. Hnce, they will switch from their initial choice of (1) to (2).

Note that not all 3-tuples correspond to sample points. For example,

• $(1, 2, 1)$ is not a sample point, because we can't reveal the box with the prize.
• $(2, 1, 1)$ is not a sample point, because we can't reveal the box the player chose.
• $(1, 1, 2), (1, 1, 3)$ is OK. The player chooses the correct box, carol reveals some box, and then the player switches.

Constructing the sample space: tree method

We build a decision tree.

where is the prize?

(prize 1)
(prize 2)
(prize 3)

player's choice

(prize 1
   (choice 1)
   (choice 2)
   (choice 3))
(prize 2
   (choice 1)
   (choice 2)
   (choice 3))
(prize 3
   (choice 1)
   (choice 2)
   (choice 3))

Which box is revealed

(prize 1
   (choice 1 
      (reveal 2)
      (reveal 3))
   (choice 2
      (reveal 3))
   (choice 3)
      (reveal 2))
(prize 2
   (choice 1
     (reveal 3)
   (choice 2
     (reveal 1)
      (reveal 3))
   (choice 3)
     (reveal 1))
(prize 3
   (choice 1
     (reveal 2))
   (choice 2
     (reveal 1))
   (choice 3)
     (reveal 1)
     (reveal 2))

Win/Loss

(prize 1
   (choice 1 
loss  (reveal 2)  
loss  (reveal 3)) 
   (choice 2
win   (reveal 3))
   (choice 3)
win   (reveal 2))
(prize 2
   (choice 1
win  (reveal 3)
   (choice 2
loss (reveal 1)
loss  (reveal 3))
   (choice 3)
win  (reveal 1))
(prize 3
   (choice 1
win  (reveal 2))
   (choice 2
win  (reveal 1))
   (choice 3)
loss (reveal 1)
loss (reveal 2))

This seems like it's 50/50! But what we're missing is the likelihood of an outcome.

Defn: Probability space

A probability space consists of a sample space (space of al outcomes) and a probability function $P$ that maps the sample space to the real numbers, such that:

• For every outcome, the probability is between zero and one.
• The sum of all the probabilities is one.

Interpretation: For every outcome, the $P(outcome)$ is the probability of that outcome happening in an experiment.

Assumptions for monty hall

• Carol put the prize uniformly randomly. Probability 1/3.
• No matter where the prize is, the player picks each box with probability 1/3.
• No matter where the prize is, the box that carol reveals will be picked uniformly randomly. Probability 1/2.

Assigning probabilities to each edge

(prize 1 [1/3]
   (choice 1 [1/3]
l  (reveal 2)   [1/2]
l  (reveal 3))  [1/2]
   (choice 2 [1/3]
w   (reveal 3)) [1]
   (choice 3) [1/3]
w   (reveal 2)) [1]
(prize 2 [1/3]
   (choice 1
w  (reveal 3)
   (choice 2
l (reveal 1)
l  (reveal 3))
   (choice 3)
w  (reveal 1))
(prize 3  [1/3]
   (choice 1
w  (reveal 2))
   (choice 2
w  (reveal 1))
   (choice 3)
l (reveal 1)
l (reveal 2))

Assigning probabilities to each outcome

• Probability for a sample point is the product of probabilities leading to the outcome

(prize 1 [1/3]
   (choice 1 [1/3]
l  (reveal 2)   [1/2]: 1/18
l  (reveal 3))  [1/2]: 1/18
   (choice 2 [1/3]
w   (reveal 3)) [1]: 1/9
   (choice 3) [1/3]
w   (reveal 2)) [1]: 1/9
...

So the probability of winning is going to be $6 \times 1/9 = \frac{2}{3}$.

Defn: Event

An event is a subset of the sample space.

• For example, $E_l$ is the event that the person loses in Monty Hall.

Probability of an event

The probability that an event $E$ occurs is the sum of the probabilities of the sample points of the event: $P(E) \equiv \sum_{e \in E} P(e)$.

What about staying?

I win $2/3$rds of the time when I switch. If I don't switch, I must have lost. So if I choose to stay, then I lose $2/3$rds of the time. We're using that

• $P(\texttt{win with switch}) = P(\texttt{lose with stick})$.

Gambing game

• Dice $A$: ${2, 6, 7}$.

\ 2  /
 \  /
6 \/ 7
  ||

it's the same on the reverse side. It's a fair dice. So the probability of getting $2$ is a third. Similarly for $6, 7$.

• Dice $B$: ${1, 5, 9 }$.

• Dice $C$: ${3, 4, 8 }$.

• We both dice. The higher dice wins. Loser pays the winner a dollar.

Analysis: Dice A v/s Dice C

• Dice $A$ followed by dice $C$:

(2
  (3
   4
   8))
(6
  (3
   4
   8))
(7
  (3
   4
   8))

• Assign winning

(2
  (3    C
   4    C
   8))  C
(6
  (3    A
   4    A
   8))  C
(7
  (3    A
   4    A
   8))  C

Each of the outcomes has a probability $1/9$, so dice $C$ wins.

Lecture 19: Conditional probability

P(A|B) where both A and B are events, read as probability of A given B.

$$ P(A|B) \equiv \frac{P(A \cap B)}{P(B)} $$

We know $B$ happens so we normalize by $B$. We then intersect $A$ with $B$ because we want both $A$ and $B$ to have happened, so we consider all outcomes that both $A$ and $B$ consider eventful, and then reweigh the probability such that our definition of "all possible outcomes" is simply "outcomes in $B$".

• A quick calculation shows us that $P(B|B) = P(B \cap B)/Pr(B) =1$.

Product Rule

$$ P(A \cap B) = P(B) P(A|B) $$

follows from the definition by rearranging.

General Product Rule

$$ P(A_1 \cap A_2 \dots A_n) = P(A_1) P(A_2 | A_1) P(A_3 | A_2 \cap A_1) P(A_4 | A_3 \cap A_2 \cap A_1) \dots P(A_n | A_1 \cap \dots \cap A_{n-1}) $$

Example 1:

In a best two out of three series, the probability of winning the first game is $1/2$. The probability of winning a game immediately after a victory is $2/3$. Probability of winning after a loss is $1/3$. What is the probability of winning given that we win in the first game?

Tree method:

(W1
  (W2) 
   (L2 
      (W3
      L3)))
(L1
  (W2) 
   (L2 
      (W3
      L3)))
(L1)

The product rule sneakily uses conditional probability! $P(W_1W_2) = P(W_1) P(W_2|W_1)$. Etc, solve the problem.

Definition: Independence

events $A$, $B$ are independent if $P(A|B) = P(A)$ or $P(B) = 0$.

Disjointness and independence

Disjoint events are never independent, because $P(A|B) = 0$ while $P(A)$ need not be zero.

What do indepdent events look like?

We know that we need $P(A|B) = P(A)$. We know that $P(A|B)$ is how much of $A$ is within $B$. So we will have $P(A|B) = P(A)$ if the space that $A$ occupies in the sample space is the same proprtion of $A$ that occupies $B$. Euphimistically, $A/S = (A \cap B)/B$.

Independence and intersection

If $A$ is independent of $B$ then $P(A\cap B) = P(A) P(B)$.

$$ \begin{aligned} P(A) = P(A|B) \text{(given)} \ P(A) = P(A \cap B) / P(B) \text{(defn of computing $P(A|B)$)} \ P(A) P(B) = P(A \cap B) \text{(rearrange)} \ \end{aligned} $$

Are these two independent?

• A = event coins match
• B = event that the first coin is heads.

Intuitively it seems that these should be dependent because knowing something about the first coin should tells us if the coins match. $P(A|B)$ is the probability that (second coin is heads) which is $1/2$. $P(A) = 1/2$.

But our intuition tells us that these should be different!

Be suspect! Try general coins

Let prob. of heads is $p$ and tails is $(1-p)$ for both coins.

$P(A|B) = p$, while $P(A) = p^2 + (1-p)^2$.

Mutual independence

Events $A_1, A_2, \dots A_n$ are mutually independent if any knowledge about any of the rest of the events tells us anything about the $i$th event.

Random variables

A random variable $R$ is a function from the sample space $S$ to $\mathbb R$. We can create equivalence classes of the fibers of $R$. Each of this is an event, since it's a subset of the sample space. Thus, $P(R = x)$ = $P(R^{-1}(x)) = \sum_{w: R(w) = x} P(w)$

Independence of random variables

$$ \forall x_1, x_2 \in \mathbb R, P(R_1 = x_1 | R_2 = x_2) = P(R_1 = x_1) $$

Slogan: No value of $R_2$ can influence any value of $R_1$.

Equivalent definition of independence:

$$ P(R_1 = x_1 \land R_2 = x_2) = P(R_1 = x_1) P(R_2 = x_2) $$

References

• Lec 18: math for computer science; elementary probability
• Lec 19: math for computer science; elementary probability
• Lec 21: math for computer science; random variables
• Problem set 10
• Problem set 11
• Problem set 12

The handshaking lemma

Concrete situation:

Let's take a graph $G \equiv (V, E)$. We can imagine that each edge has a potential of $2$. We can redistribute this potential, by providing a potential of $1$ to each of the vertices incident on the edge. This gives us the calculation that the total potential is $2|E|$. But each vertex is assigned a potential of $1$ for each edge incident on it. Thus, the total potential is $\sum_v \texttt{degree}(v)$. This gives the equality $\sum_i \texttt{degree}(v) = 2|E|$.

Thus, if each of the degrees are odd, considering modulo 2, the LHS becomes $\sum_v 1 = |V|$ and the RHS becomes $0$. Thus we have that $|V| = 0$ (mod 2), or the number of vertices remains even.

I learnt of this nice way of thinking about it in terms of potentials when reading a generalization to simplicial complexes.

References

• The amazing world of simplicial complexes

Git for pure mathematicians

What is git? It's not a version control system. It's an interface to work with torsors. We have a space of files. We can manipulate "differences of files", which are represented by patches/diffs. git's model provides us tools to work with this space of files.

We have two spaces, and a rooted DAG that connects to two spaces:

• A space of files.
• A space of diffs which forms a monoid with a monoid action on the space of files.
• A DAG where each node is a diff. The root note in the DAG is the empty diff.

Mutorch

#!/usr/bin/env python3

# x2, w1, w2 are Leaf variables
# x1 = f(w1, w2)
# y = g(x1, x2)
# loss = h(y)


# BACKPROP [reverse mode AD]
# ==========================
# t is a hallucinated variable.
# y = f(x)
# GIVEN: dt/dy
# TO FIND: dt/dx
# dt/dx = dt/dy * dy/dx
# dt/dloss 
# t = loss
# dt/dloss = dloss/dloss = 1


# y1 = f(x1, x2, x3)
# y2 = g(x1, x2, x3)

# FORWARD MODE: [Tangent space] ---- objects of the does nothing at all :$\texttt{form (partial f/partial x)
# total gradient of x1: df/dx1 + dg/dx1
# total gradient of x2: df/dx2 + dg/dx2
# total gradient of x3: df/dx3 + dg/dx3

# l = r cos(theta)
# dl = dr cos(theta) + rsin(theta) dtheta 
# dl/dtheta = dr/dtheta cos(theta) + rsin(theta) dtheta/dtheta
# dl/dtheta =   0       * .......  + rsin(theta) * 1

# dl/dr = dr/dr cos(theta) + rsin(theta) dtheta/dr
# dl/dr = cos(theta) +      .............*0

# REVERSE MODE: [CoTangent space] --- objects of the form df
# total gradient of y1: dy1 = (df/dx1)dx1 + (df/dx2)dx2  + (df/dx3)dx3 
# total gradient of y2: dy2 = (dg/dx1)dx1 + (dg/dx2)dx2  + (dg/dx3)dx3
# HALLUCINATED T:
#    y1 = f(x1, x2, x3)
#    GIVEN:   dt/dy1 [output]
#    TO FIND: dt/dx1, dt/dx2, dt/dx3 [inputs]
#    SOLN:    dt/dxi = dt/dy * dy/dxi 
#                    = dt/dy * df/dxi 
import pudb

class Expr:
    def __mul__(self, other):
        return Mul(self, other)
    def __add__(self, other):
        return Add(self, other)

    def clear_grad(self):
        pass

class Var(Expr):
    def __init__(self, name, val):
        self.name = name
        self.val = val
        self._grad = 0
    def __str__(self):
        return "(var-%s | %s)" % (self.name, self.val)
    def __repr__(self):
        return self.__str__()

    def clear_grad(self):
        self._grad = 0

    def backprop(self, dt_doutput):
        self._grad += dt_doutput

    def grad(self):
        return self._grad

class Mul(Expr):
    def __init__(self, lhs, rhs):
        self.lhs = lhs
        self.rhs = rhs
        self.val = self.lhs.val * self.rhs.val
    def __str__(self):
        return "(* %s %s | %s)" % (self.lhs, self.rhs, self.val)
    def __repr__(self):
        return self.__str__()

    #         -------- input1
    #   S    /
    #  ---> v 
    #  <--output *
    #      ^
    #       \_________ input2
    # think in terms of sensitivity.
    # - output has S sensitivity to something,
    # - output = input1 + input2
    # - how much sensitivity does input1 have to S?
    # - the same (S), because "sensitivity" is linear [a conjecture/axiom]
    # output = f(input1, input2); f(input1, input2) = input1 + input2 
    def backprop(self, dt_output):
        # dt/dinput1 = dt/doutput * ddoutput/dinput1 = 
        #            = dt/doutput * d(f(input1, input2))/dinput1
        #            = dt/doutput * d(input1 * input2)/dinput1
        #            = dt/doutput * input2
        self.lhs.backprop(dt_output * self.rhs.val)
        self.rhs.backprop(dt_output * self.lhs.val)

# a = ...   ^
# b = ...   ^
# c = a + b ^
# 
class Add(Expr):
    def __init__(self, lhs, rhs):
        self.lhs = lhs
        self.rhs = rhs
        self.val = self.lhs.val + self.rhs.val
    def __str__(self):
        return "(+ %s %s | %s)" % (self.lhs, self.rhs, self.val)
    def __repr__(self):
        return self.__str__()

    #         -------- input1
    #   S    /
    #  ---> v 
    #  <--output
    #      ^
    #       \_________ input2
    # think in terms of sensitivity.
    # - output has S sensitivity to something,
    # - output = input1 + input2
    # - how much sensitivity does input1 have to S?
    # - the same (S), because "sensitivity" is linear [a conjecture/axiom]
    # output = f(input1, input2); f(input1, input2) = input1 + input2 
    def backprop(self, dt_output):
        # dt/dinput1 = dt/doutput * ddoutput/dinput1 = 
        #            = dt/doutput * d(f(input1, input2))/dinput1
        #            = dt/doutput * d(input1 + input2)/dinput1
        #            = dt/doutput * 1
        self.lhs.backprop(dt_output * 1)
        self.rhs.backprop(dt_output * 1)

class Max(Expr):
    def __init__(self, lhs, rhs):
        self.lhs = lhs
        self.rhs = rhs
        self.val = max(self.lhs.val, self.rhs.val)
    def __str__(self):
        return "(max %s %s | %s)" % (self.lhs, self.rhs, self.val)
    def __repr__(self):
        return self.__str__()

    def backprop(self, dt_output):
        # dt/dinput1 = dt/doutput * doutput/dinput 1 
        #            = dt/doutput *d max(input1, input2)/dinput1
        #            = |dt/doutput *d input1/dinput1 [if input1 > input2] = 1
        #            = |dt/doutput *d input2/dinput1 [if input2 > input1] = 0
        if self.val == self.lhs.val:
            self.lhs.backprop(dt_output * 1)
        else:
            self.rhs.backprop(dt_output * 1)

x = Var("x", 10)
print("x: %s" % x)
y = Var("y", 20)
p = Var("p", 30)
print("y: %s" % y)
z0 = Mul(x, x)
print("z0: %s" % z0)
z1 = Add(z0, y)
print("z1: %s" % z1)

# z1 = x*x+y 
# dz1/dx = 2x 
# dz1/dy = 1
# dz1/dp = 0
# z1.clear_grad()
z1.backprop(1) #t = z1
print("dz/dx: %s" % x.grad())
print("dz/dy: %s" % y.grad())
print("dz/dp: %s" % p.grad())

x.clear_grad()
y.clear_grad()
z1.backprop(1) #t = z1
print("dz/dx: %s" % x.grad())
print("dz/dy: %s" % y.grad())

Computing the smith normal form

#!/usr/bin/env python3.6
# Smith normal form
import numpy as np
from numpy import *
import math

def row_for_var(xs, vi: int):
    NEQNS, NVARS = xs.shape
    for r in range(vi, NVARS):
        if xs[r][vi] != 0: return r
# return numbers (ax, ay) such that ax*x - ay*y = 0
def elim_scale_factor(x: int, y: int): return (y, x)

def smith_normal_form(xs, ys):
    NEQNS, NVARS = xs.shape
    assert(NEQNS == ys.shape[0])


    # eliminate variable 'vi' by finding a row 'r' and then using the row
    # to eliminate.
    for vi in range(NVARS):
        ri = row_for_var(xs, vi)
        if ri is None: 
            return (f"unable to find non-zero row for variable: {vi}")
        print(f"-eliminating variable({vi}) using row ({ri}:{xs[ri]})")
        # eliminate all other rows using this row
        for r2 in range(NEQNS):
            # skip the eqn ri.
            if r2 == ri: continue
            # eliminate.
            (scale_ri, scale_r2) = elim_scale_factor(xs[ri][vi], xs[r2][vi])

            print(f"-computing xs[{r2}] = {scale_r2}*xs[{r2}]:{xs[r2]} - {scale_ri}*xs[{ri}]:{xs[ri]}")
            xs[r2] = scale_r2 * xs[r2] - scale_ri * xs[ri]
            ys[r2] = scale_r2 * ys[r2] - scale_ri * ys[ri]
        print(f"-state after eliminating variable({vi})")
        print(f"xs:\n{xs}\n\nys:{ys}")

    sols = [None for _ in range(NVARS)]
    for vi in range(NVARS):
        r = row_for_var(xs, vi)
        if r is None:
            print(f"unable to find row for variable {vi}")
            return None
        assert(xs[r][vi] != 0)
        if ys[r] % xs[r][vi] != 0:
            print(f"unable to solve eqn for variable {vi}: xs:{xs[r]} = y:{ys[r]}")
            return None
        else:
            sols[vi] = ys[r] // xs[r][vi]

    # now check solutions if we have more equations than solutions
    for r in range(NEQNS):
        lhs = 0
        for i in range(NVARS): lhs += xs[r][i] * sols[i]
        if lhs != ys[r]:
            print(f"-solution vector sols:{sols} cannot satisfy row xs[{r}] = ys[{r}]:{xs[r]} = {ys[i]}")
            return None
        

    return sols

# consistent system
# x = 6, y = 4
# x + y = 10
# x - y = 2
xs = np.asarray([[1, 1], [1, -1]])
ys = np.asarray([10, 2]) 
print("## CONSISTENT ##")
out = smith_normal_form(xs,ys)
print("xs:\n%s\n\nys:\n%s\n\nsoln:\n%s" % (xs, ys, out,))


# consistent, over-determined system
# x = 6, y = 4
# x + y = 10
# x - y = 2
# x + 2y = 14
xs = np.asarray([[1, 1], [1, -1], [1, 2]])
ys = np.asarray([10, 2, 14]) 
print("## CONSISTENT OVER DETERMINED ##")
out = smith_normal_form(xs,ys)
print("xs:\n%s\n\nys:\n%s\n\nsoln:\n%s" % (xs, ys, out,))

# consistent, under-determined system
# x = 6, y = 4, z = 1
# x + y + z = 11
# x - y + z = 3
xs = np.asarray([[1, 1], [1, -1], [1, 2]])
ys = np.asarray([10, 2, 14]) 
print("## CONSISTENT UNDER DETERMINED ##")
out = smith_normal_form(xs,ys)
print("xs:\n%s\n\nys:\n%s\n\nsoln:\n%s" % (xs, ys, out,))


# inconsistent system
# x = 6, y = 4 
# x + y = 10
# x - y = 2
# x + 2y = 1 <- INCONSTENT
xs = np.asarray([[1, 1], [1, -1], [1, 2]])
ys = np.asarray([10, 2, 1]) 
print("## INCONSISTENT (OVER DETERMINED) ##")
out = smith_normal_form(xs,ys)

# inconsistent system
# x + y = 10
# x - y = 2
xs = np.asarray([[1, -1], [1, 2], [1, 1]])
ys = np.asarray([10, 2, 1]) 
print("## INCONSISTENT (OVER DETERMINED) ##")
out = smith_normal_form(xs,ys)


# consistent system over Q, not Z
# x = y = 0.5
# x + y = 1
# x - y = 0
xs = np.asarray([[1, 1], [1, -1]])
ys = np.asarray([1, 0]) 
print("## INCONSISTENT (SOLVABLE OVER Q NOT Z) ##")
out = smith_normal_form(xs,ys)

Laziness for C programmers

Side node: nonsrict versus lazy (This section can be skipped)

I will use the word non-strict throughout, and not lazy. Roughly speaking, lazy is more of an implementation detail that guarantees that a value that is once computed is cached. (operational semantics)

non-strict is a evaluation order detail that guarantees that values are not evaluated until there are truly required. (denotational semantics).

lazy is one way to implement non-strict.

This is pure pedantry, but I'd like to keep it straight, since there seems to be a lot of confusion involving the two words in general.

Showing off non-strictness:

We first need a toy example to work with to explain the fundamentals of non-strict evaluation, so let's consider the example below. I'll explain the case construct which is explained below. Don't worry if ato lazy evaluation "looks weird", it feels that way to everyone till one plays around with it for a while!

We will interpret this example as both a strict program and a non-strict program. This will show us that we obtain different outputs on applying different interpretations.

We distinguish between primitive values (integers such as 1, 2, 3) and boxed values (functions, data structures). Boxed values can be evaluated non-stricly. Primitive values do not need evaluation: they are primitive.

Code

-- Lines starting with a `--` are comments.
-- K is a function that takes two arguments, `x` and `y`, that are both boxed values.
-- K returns the first argument, `x`, ignoring the second argument, `y`.
-- Fun fact: K comes for the K combinator in lambda calculus.
kCombinator :: Boxed -> Boxed -> Boxed
kCombinator x y = x

-- one is a function that returns the value 1# (primitive 1)
one :: PrimInt
one = 1

-- Loopy is a function that takes zero arguments, and tries to return a boxed value.
-- Loopy invokes itself, resulting in an infinite loop, so it does not actually return.
loopy :: Boxed
loopy = loopy

-- main is our program entry point.
-- main takes no arguments, and returns nothing
main :: Void
main = case kCombinator one loopy of -- force K to be evaluated with a `case`
            kret -> case kret of  -- Force evaluation
                    i -> printPrimInt i -- Call the forced value of `kret` as `i` and then print it.

A quick explanation about case:

case is a language construct that forces evaluation. In general, no value is evaluated unless it is forced by a case.

Analysing the example: The strict interpretation

If we were coming from a strict world, we would have assumed that the expression K one loopy would first try to evaluate the arguments, one and loopy. Evaluating one would return the primitive value 1, so this has no problem.

On trying to evaluate loopy, we would need to re-evaluate loopy, and so on ad infitum, which would cause this program to never halt.

This is because, as programmers coming from a strict world, we assume that values are evaluated as soon as possible.

So, the output of this program is to have the program infinite-loop for ever, under the strict interpretation.

Analysing the example: The non-strict interpretation:

In the non-strict world, we try to evaluate K(1, loopy) since we are asked the result of it by the case expression. However, we do not try to evaluate loopy, since no one has asked what it's value is!

Now, we know that

kCombinator x y = x

Therefore,

kCombinator one loopy = one

regardless of what value loopy held.

So, at the case expression:

main = case K(one, loopy) of -- force K to be evaluated with a `case`
>>>         kret -> ...

kret = one, we can continue with the computation.

main :: () -> Void
main = case kCombinator one loopy of -- force K to be evaluated with a `case`
            kret -> case kret of  -- Call the return value of K as `x`, and force evaluation.
                       i -> printPrimInt i -- Call the vreturn value of `x` as `primx` and then print it.

Here, we force kret (which has value one) to be evaluated with case kret of.... since one = 1, i is bound to the value 1. Once i is returned, we print it out with printPrimInt(primx).

The output of the program under non-strict interpretation is for it to print out 1.

Where does the difference come from?

Clearly, there is a divide: strict evaluation tells us that this program should never halt. Non-strict evaluation tells us that this program will print an output!

To formalize a notion of strictness, we need a notion of bottom (_|_).

A value is said to be bottom if in trying to evaluate it, we reach an undefined state. (TODO: refine this, ask ben).

Now, if a function is strict, it would first evaluate its arguments and then compute the result. So, if a strict function is given a value that is bottom, the function will try to evaluate the argument, resulting in the computation screwing up, causing the output of the whole function to be bottom.

Formally, a function f is strict iff (if and only if) f(bottom) = bottom.

Conversely, a non-strict function does not need to evaluate its arguments if it does not use them, as in the case of K 1 loopy. In this case, f(bottom) need not be equal to bottom.

Formally, a function f is non-strict iff (if and only if) f(bottom) /= bottom.

As Paul Halmos says

"A good stack of examples, as large as possible, is indispensable for a thorough understanding of any concept, and when I want to learn something new, I make it my first job to build one.". Let us consider some examples.

• id

id x = x

id (3) = 1
id (bottom) = bottom

id is strict, since id(bottom) = bottom.

• const

const_one x = 1

const_one(bottom) = 1
const_one(3) = 1

const_one is not strict, as const_one(bottom) /= bottom.

• K

K x y = x

K 1 2 = 1
K 1 bottom = 1
K bottom 2 = bottom

Note that K(bottom, y) = bottom, so K is strict in its first argument, and K(x, bottom) /= bottom, so K is non-strict in its second argument.

This is a neat example showing how a function can be strict and lazy in different arguments of the function.

Compiling non-strictness, v1:

How does GHC compile non-strictness?

GHC (the Glasgow haskell compiler) internally uses multiple intermediate representations, in order of original, to what is finally produced:

• Haskell (the source language)
• Core (a minimal set of constructs to represent the source language)
• STG (Spineless tagless G-machine, a low-level intermediate representation that accurately captures non-strict evaluation)
• C-- (A C-like language with GHC-specific customization to support platform independent code generation).
• Assembly

Here, I will show how to lower simple non-strict programs from a fictitous Core like language down to C , while skipping STG, since it doesn't really add anything to the high-level discussion at this point.

Our example of compiling non-strictness

Now, we need a strategy to compile the non-strict version of our program. Clearly, C cannot express laziness directly, so we need some other mechanism to implement this. I will first code-dump, and then explain as we go along.

Executable repl.it:

<iframe height="400px" width="100%" src="https://repl.it/@bollu/Compiling-non-strict-programs-on-the-call-stack?lite=true" scrolling="no" frameborder="no" allowtransparency="true" allowfullscreen="true" sandbox="allow-forms allow-pointer-lock allow-popups allow-same-origin allow-scripts allow-modals"></iframe>

Source code

#include <assert.h>
#include <stdio.h>

/* a boxed value is a function that can be executed to compute something.
* We make the return value `void` on purpose. This needs to be typecast to a concrete
* Boxed type to get a value out of it: eg, typecast to BoxedInt.
*/
typedef void (*Boxed)();

/* A boxed int, that on evaluation yields an int*/
typedef int (*BoxedInt)();

/* one = 1# */
int one() {
    return 1;
}

/* bottom = bottom */
void bottom() {
    printf("in function: %s\n", __FUNCTION__);
    bottom();
}

/* K x y = x */
Boxed K(Boxed x, Boxed y) {
  return x;
}

/*
main :: () -> Void
main = case K(one, loopy) of -- force K to be evaluated with a `case`
            kret -> case kret of  -- Call the return value of K as `x`, and force evaluation.
                    i -> printPrimInt(i) -- Call the vreturn value of `x` as `primx` and then print it.
*/
int main() {
    Boxed kret = K((Boxed)one, (Boxed)bottom);
    int i = (*(BoxedInt)kret)();
    printf("%d", i);
    return 1;
}

We convert every possibly lazy value into a Boxed value, which is a function pointer that knows how to compute the underlying value. When the lazy value is forced by a case, we call the Boxed function to compute the output.

This is a straightforward way to encode non-strictness in C. However, do note that this is not lazy, because a value could get recomputed many times. Laziness guarantees that a value is only computed once and is later memoized.

Compiling with a custom call stack / continuations

As one may notice, we currenly use the native call stack every time we force a lazy value. However, in doing so, we might actually run out of stack space, which is undesirable. Haskell programs like to have "deep" chains of values being forced, so we would quite likely run out of stack space.

Therefore, GHC opts to manage its own call stack on the heap. The generated code looks as you would imagine: we maintain a stack of function pointers + auxiliary data ( stack saved values), and we push and pop over this "stack". When we run out of space, we <find correct way to use mmap> to increase our "stack" size.

I've played around with this value a little bit, and have found that the modern stack size is quite large: IIRC, It allowed me to allocate ~26 GB. I believe that the amount it lets you allocate is tied directly to the amount of physical memory + swap you have. I'm not too sure, however. So, for my haskell compiler, sxhc, I am considering cheating and just using the stack directly.

Code for the same example (with the K combinator) is provided here.

Executable repl.it:

<iframe height="1000px" width="100%" src="https://repl.it/@bollu/Compiling-programs-with-continuations?lite=true" scrolling="no" frameborder="no" allowtransparency="true" allowfullscreen="true" sandbox="allow-forms allow-pointer-lock allow-popups allow-same-origin allow-scripts allow-modals"></iframe>

Source code

#include <assert.h>
#include <stdio.h>
#define STACK_SIZE 50000

/* a boxed value is a function that can be executed to compute something. */
typedef void (*Boxed)();

/* a return continuation that receives a boxed value. */
typedef void (*BoxedContinuation)(Boxed);

/* A return continuation that receives an int value. */
typedef void (*IntContinuation)(int);

/* Custom stack allocated on the .data section*/
void *stack[STACK_SIZE];

/* Stack pointer */
int sp = 0;

/* Push a continuation `cont` */
void pushContinuation(void *cont) {
    assert(sp >= 0);
    assert(sp < STACK_SIZE);
    stack[sp] = cont;
    sp++;
}

/* Pop a continuation frame. */
void *popContinuation() {
    assert(sp < STACK_SIZE);
    assert(sp >= 0);
    sp--;
    void *cont = stack[sp];
    return cont;
}

/* one = 1# */
void one() {
    printf("in function: %s\n", __FUNCTION__);
    void *f = popContinuation();
    (*(IntContinuation)(f))(1);
}

/* bottom = bottom */
void bottom() {
    printf("in function: %s\n", __FUNCTION__);
    bottom();
}

/* K x y = x */
void K(Boxed x, Boxed y) {
    printf("in function: %s\n", __FUNCTION__);
    void *f = popContinuation();
    (*(BoxedContinuation)(f))(x);
}

void XForceContinuation(int i) {
    printf("in function: %s\n", __FUNCTION__);
    printf("%d", i);
}

void KContinuation(Boxed x) {
    printf("in function: %s\n", __FUNCTION__);
    pushContinuation((void *)XForceContinuation);
    x();
}

int main() {
    printf("in function: %s\n", __FUNCTION__);
    pushContinuation((void *)KContinuation);
    K(one, bottom);
    return 0;
}

we maintain our own "call stack" of continuations. These continuations are precisely the parts of the code that deal with the return value of a case. ever

case x of
    xeval -> expr

compiles to:

pushContinuation(XEvalContinuation);
x()

That is, push a continuation, and then "enter" into x.

One might have a question: does this still not use the call stack? There is a function call at the end of most functions in the source code, so in theory, we are using the call stack, right? The answer is no. It's thanks to a neat optimisation technique called tail call elimination. The observation is that after the call, there is no more code to execute in the caller. So, by playing some stack tricks, one can convert a call to a jump.

Remember, a call instruction uses the stack to setup a stack frame, under the assumption that we will ret at some point. But, clearly, under our compilation model, we will never ret, simply call more functions. So, we don't need the state maintained by a call. We can simply jmp.

Wrapping up

I hope I've managed to convey the essence of how to compile Haskell. I skipped a couple of things:

• haskell data types: sum and product types. These are straightforward, they just compiled to tagged structs.
• let bindings: These too are straightforward, but come with certain retrictions in STG. It's nothing groundbreaking,and is well written in the paper.
• Black holes: Currently, we are not truly lazy, in that we do not update values once they are computed.
• GC: how to weave the GC through the computation is somewhat non-trivial.

All of this is documented in the excellent paper: Implementing lazy languages on stock hardware.

I am considering extending this blog post that expands on these ideas. If there is interest, please do e-mail me at [email protected].

Exact sequence of pointed sets

This was a shower thought. I don't even if these form an abelian category. Let's assume we have pointed sets, where every set has a distinguished element $$. $p$ will be analogous to the zero of an abelian group. We will also allow multi-functions, where a function can have multiple outputs. Now let's consider two sets, $A, B$ along with their 'smash union' $A \vee B$ where we take the disjoint union of $A, B$ with a smashed $$. To be very formal:

$$ A \vee B = {0} \times (A - { * }) \cup {1}\times (B - { * }) \cup { * } $$

We now consider the exact sequence:

$$ (A \cap B, *) \xrightarrow{\Delta} (A \vee B, *) \xrightarrow{\pi} (A \cup B, *) $$

with the maps as: $$ \begin{aligned} &ab \in A \cap B \xmapsto{\Delta} (0, ab), (1, ab) \in A \vee B \ &(0, a) \in A \vee B \xmapsto{\pi} \begin{cases}

• & \text{if } a \in B \ a &\text{otherwise} \ \end{cases} \ &(1, b) \in A \vee B \xmapsto{\pi} \begin{cases}
• & \text{if } b \in A \ b &\text{otherwise} \ \end{cases} \ \end{aligned} $$

• We note that $\Delta$ is a multi-function, because it produces as output both $(0, ab)$ and $(1, ab)$.
• $\ker(\pi) = \pi^{-1}(*) = { (0, a) : a \in B } \cup { (1, b) : b \in A }$
• Since it's tagged $(0, a)$, we know that $a \in A$. Similarly, we know that $b \in B$.
• Hence, write $\ker(\pi) = { (0, ab), (1, ab) : ab \in A \cap B } = im(\Delta)$

This exact sequence also naturally motivates one to consider $A \cup B - A \cap B = A \Delta B$, the symmetric difference. It also gives the nice counting formula $|A \vee B| = |A \cap B| + |A \cup B|$, also known as inclusion-exclusion.

I wonder if it's possible to recover incidence algebraic derivations from this formuation?

Variation on the theme: direct product

This version seems wrong to me, but I can't tell what's wrong. Writing it down:

$$ \begin{aligned} (A \cap B, ) \xrightarrow{\Delta} (A \times B, (, *)) \xrightarrow{\pi} (A \cup B, *) \end{aligned} $$

with the maps as:

$$ \begin{aligned} &ab \in A \cap B \xmapsto{\Delta} (ab, ab) \in A \times B \ &(a, b) \in A \times B \xmapsto{\pi} \begin{cases}

• & \text{if } a = b \ a, b &\text{otherwise} \ \end{cases} \ \end{aligned} $$

One can see that:

• $A \cap B \xrightarrow{\Delta} A \times B$ is injective
• $A \cap B \xrightarrow{\pi} A \cup B$ is surjective
• $ker(\pi) = \pi^{-1}(*) = { (a, b) : a \in A, b \in B, a = b } = im(\Delta)$

Note that to get the last equivalence, we do not consider elements like $\pi(a, ) = a, $ to be a pre-image of $$, because they don't exact ly map into $$ [pun intended].

What is a syzygy?

Word comes from greek word for "yoke" . If we have two oxen pulling, we yoke them together to make it easier for them to pull.

The ring of invariants

Rotations of $\mathbb R^3$: We have a group $SO(3)$ which is acting on a vector space $\mathbb R^3$. This preserves the length, so it preserves the polynomial $x^2 + y^2 + z^2$. This polynomial $x^2 + y^2 + z^2$ is said to be the invariant polynomial of the group $SO(3)$ acting on the vector space $\mathbb R^3$.

• But what does $x, y, z$ even mean? well, they are linear function $x, y, z: \mathbb R^3 \rightarrow \mathbb R$. So $x^2 + y^2 + z^2$ is a "polynomial" of these linear functions.

How does a group act on polynomials?

• If $G$ acts on $V$, how does $G$ act on the polynomial functions $V \rightarrow \mathbb R$?
• In general, if we have a function $f: X \rightarrow Y$ where $g$ acts on $X$ and $Y$ (in our case, $G$ acts trivially on $Y=\mathbb R$), what is $g(f)$?
• We define $(gf)(x) \equiv g (f(g^{-1}(x)))$.
• What is the $g^{-1}$? We should write $(gf)(gx) = g(fx)$. This is like $g(ab) = g(a) g(b)$. We want to get $(gf)(x) = (gf)(g(g^{-1}x) = g(f(g^{-1}x))$.
• If we miss out $g^{-1}$ we get a mess. Let's temporarily define $(gf)(x) = f(g(x))$. Consider $(gh)f(x) = f(ghx)$. But we can also take this as $(gh)(f(x)) = g((hf)(x)) = (hf)(gx) = f(hgx)$. This is absurd as it gives $f(ghx) = f(hgx)$.

Determinants

We have $SL_n(k)$ acting on $k^n$, it acts transitively, so there's no interesting non-constant invariants. On the other hand, we can have $SL_n(k)$ act on $\oplus_{i=1}^n k^n$. So if $n=2$ we have:

$$ \begin{bmatrix} a & b \ c & d \end{bmatrix} $$

acting on:

$$ \begin{bmatrix} x_1 & y_1 \ x_2 & y_2 \end{bmatrix} $$

This action preserves the polynomial $x_1 y_2 - x_2 y_1$, aka the determinant. anything that ends with an "-ant" tends to be an "invari-ant" (resultant, discriminant)

$S_n$ acting on $\mathbb C^n$ by permuting coordinates.

Polynomials are functions $\mathbb C[x_1, \dots, x_n]$. Symmetric group acts on polynomials by permuting $x_1, \dots, x_n$. What are the invariant polynomials?

• $e_1 \equiv x_1 + x_2 + \dots x_n$
• $e_2 \equiv x_1 x_2 + x_1 x_3 + \dots + x_{n-1} x_n$.
• $e_n \equiv x_1 x_2 \dots x_n$.

These are the famous elementary symmetric functions. If we think of $(y - x_1) (y - x_2) \dots (y - x_n) = y^n - e_1 y^{n-1} + \dots e_n$.

• The basic theory of symmetric functions says that every invariant polynomial in $x_1, \dots x_n$ is a polynomial in $e_1, \dots, e_n$.

Proof of elementary theorem

Define an ordering on the monomials; order by lex order. Define $x_1^{m_1} x_2^{m_2} > x_1^{n_1} x_2^{n_2} \dots$ iff either $m_1 > n_1$ or $m_1 = n_1 \land m_2 > n_2$ or $m_1 = n_1 \land m_2 = n_2 \land m_3 > n_3$ and so on.

Suppose $f \in \mathbb C[x_1, \dots, x_n]$ is invariant. Look at the biggest monomial in $f$. Suppose it is $x_1^{n_1} x_2^{n_2} \dots$. We subtract:

$$ \begin{aligned} P \equiv &(x_1 + x_2 \dots)^{n_1 - n_2} \ &\times (x_1 x_2 + x_1 x_2 \dots)^{n_2 - n_3} \ &\times (x_1 x_2 x_3 + x_1 x_2 x_4 \dots)^{n_3 - n_4} \ \end{aligned} $$

This kills of the biggest monomial in $f$. If $f$ is symmetric, Then we can order the term we choose such that $n_1 \geq n_2 \geq n_3 \dots$. We need this to keep the terms $(n_1 - n_2), (n_2 - n_3), \dots$ to be positive. So we have now killed off the largest term of $f$. Keep doing this to kill of $f$ completely.

This means that the invariants of $S_n$ acting on $\mathbb C^n$ are a finitely generated algebra over $\mathbb C$. So we have a finite number of generating invariants such that every invariant can be written as a polynomial of the generating invariants with coefficients in $\mathbb C$. This is the first non-trivial example of invariants being finitely generated.

The algebra of invariants is a polynomial ring over $e_1, \dots, e_n$. This means that there are no non-trivial-relations between $e_1, e_2, \dots, e_n$. This is unusual; usually the ring of generators will be complicated. This simiplicity tends to happen if $G$ is a reflection group. We haven't seen what a syzygy is yet; We'll come to that.

Complicated ring of invariants

Let $A_n$ (even permutations). Consider the polynomial $\Delta \equiv \prod_{i < j} (x_i - x_j)$ This is called as the discriminant. This looks like $(x_1 - x_2)$, $(x_1 - x_2)(x_1 - x_3)(x_2 - x_3)$, etc. When $S_n$ acts on $\Delta$, it either keeps the sign the same or changes the sign. $A_n$ is the subgroup of $S_n$ that keeps the sign fixed.

What are the invariants of $A_n$? It's going to be all the invariants of $S_n$, $e_1, \dots, e_n$, plus $\Delta$ (because we defined $A_n$ to stabilize $\Delta$). There are no relations between $e_1, \dots, e_n$. But there are relations between $\Delta^2$ and $e_1, \dots, e_n$ because $\Delta^2$ is a symmetric polynomial.

Working this out for $n=2$,we get $\Delta^2 = (x_1 - x_2)^2 = (x_1 + x_2)^2 - 4 x_1 x_2 = e_1^2 - 4 e_1 e_2$. When $n$ gets larger, we can still express $\Delta^2$ in terms of the symmetric polynomials, but it's frightfully complicated.

This phenomenon is an example of a Syzygy. For $A_n$, the ring of invariants is finitely generated by $(e_1, \dots, e_n, \Delta)$. There is a non-trivial relation where $\Delta^2 - poly(e_1, \dots, e_n) = 0$. So this ring is not a polynomial ring. This is a first-order Syzygy. Things can get more complicated!

Second order Syzygy

Take $Z/3Z$ act on $\mathbb C^2$. Let $s$ be the generator of $Z/3Z$. We define the action as $s(x, y) = (\omega x, \omega y)$ where $\omega$ is the cube root of unity. We have $x^ay^b$ is invariant if $(a + b)$ is divisible by $3$, since we will just get $\omega^3 = 1$.

So the ring is generated by the monomials $(z_0, z_1, z_2, z_3) \equiv (x^3, x^2y, xy^2, y^3)$. Clearly, these have relations between them. For example:

• $z_0 z_2 = x^4y^2 = z_1^2$. So $z_0 z_2 - z_1^2 = 0$.
• $z_1 z_3 x^2y^4 = z_2^2$. So $z_1 z_3 - z_2^2 = 0$.
• $z_0 z_3 = x^3y^3 = z_1 z_2$. So $z_0 z_3 - z_1 z_2 = 0$.

We have 3 first-order syzygies as written above. Things are more complicated than that. We can write the syzygies as:

• $p_1 \equiv z_0 z_2 - z_1^2$.
• $p_2 \equiv z_1 z_3 - z_2^2$.
• $p_3 \equiv z_0 z_3 - z_1 z_2$.

We have $z_0 z_2$ in $p_1$. Let's try to cancel it with the $z_2^2$ in $p_2$. So we consider:

$$ \begin{aligned} & z_2 p_1 + z_0 p_2 \ &= z_2 (z_0 z_2 - z_1^2) + z_0 (z_1 z_3 - z_2^2) \ &= (z_0 z_2^2 - z_2 z_1^2) + (z_0 z_1 z_3 - z_0 z_2^2) \ &= z_0 z_1 z_3 - z_2 z_1^2 \ &= z_1(z_0 z_3 - z_1 z_2) \ &= z_1 p_3 \end{aligned} $$

So we have non-trivial relations between $p_1, p_2, p_3$! This is a second order syzygy, a sygyzy between syzygies.

We have a ring $R \equiv k[z_0, z_1, z_2, z_3]$. We have a map $R \rightarrow \texttt{invariants}$. This has a nontrivial kernel, and this kernel is spanned by $(p_1, p_2, p_3) \simeq R^3$. But this itself has a kernel $q = z_1 p_1 + z_2 p_2 + z_3 p_3$. So there's an exact sequence:

$$ \begin{aligned} 0 \rightarrow R^1 \rightarrow R^3 \rightarrow R=k[z_0, z_1, z_2, z_3] \rightarrow \texttt{invariants} \end{aligned} $$

In general, we get an invariant ring of linear maps that are invariant under the group action. We have polynomials $R \equiv k[z_0, z_1, \dots]$ that map onto the invariant ring. We have relationships between the $z_0, \dots, z_n$. This gives us a sequence of syzygies. We have many questions:

1. Is $R$ finitely generated as a $k$ algebra? Can we find a finite number of generators?
2. Is $R^m$ finitely generated (the syzygies as an $R$-MODULE)? To recall the difference, see that $k[x]$ is finitely generated as an ALGEBRA by $(k, x)$ since we can multiply the $x$s. It's not finitely generated as a MODULE as we need to take all powers of $x$: $(x^0, x^1, \dots)$.
3. Is this SEQUENCE of sygyzy modulues FINITE?
4. Hilbert showed that the answer is YES if $G$ is reductive and $k$ has characteristic zero. We will do a special case of $G$ finite group.

We can see why a syzygy is called such; The second order sygyzy "yokes" the first order sygyzy. It ties together the polynomials in the first order syzygy the same way oxen are yoked by a syzygy.

References

• Richard E Borcherds: Commutative Algebra, lecture 3

Under the spell of Leibniz's dream

• Link to the article by djikstra
• monochrom's favourite work on djikstra

I found it very quotable. I'm posting some quotes below.

• On applied versus pure mathematics:

An important side-effect of the hard times was the creation of a spiritual climate in which the distinction between pure and applied science had vanished: of all the things you could do, you just did the most urgent one, and the development of some urgently needed theory was often the most practical thing to do.

• On 'applied institutes':

The worst thing with institutes explicitly devoted to applied science is that they tend to become institutes of second-rate theory.

• On the artificial divide between theory and applied sections of university:

These days there is so much obsession with application that, if the University is not careful, external forces, which do make the distinction, will drive a wedge between "theory" and "practice" and may try to banish the "theorists" to a ghetto of separate departments and separate buildings. A simple extrapolation will tell us that in due time the isolated practitioners will have little to apply; this is well-known, but has never prevented the financial mind from killing the goose that lays the golden eggs.

• On programming as typing:

Needless to say, this confusion between the score and the composition led to an underestimation of the intellectual challenges programming presents

• On hilbert and axiomatics:

Hilbert's revolution was in any case to redefine "proof" to become a completely rigorous notion, totally different from the psycho/sociological "A proof is something that convinces other mathematicians."

Normal operators: Decomposition into Hermitian operators

Given a normal operator $A$, we can always decompose it $A = B + iC$ where $B = B^{\dagger}$, $C = C^\dagger$, and $[B, C] = 0$.

This means that we can define 'complex measurements' using a normal operator, because a normal operator has full complex spectrum. Since we can always decompose such an operator $A$ into two hermitian operators $B, C$ that commute, we can diagonalize $B, C$ simultaneously and thereby measure $B, C$ simultaneously.

So extending to "complex measurements" gives us no more power than staying at "real measurements"

Decomposing a normal operator

Assume we have a normal operator $A$. Write the operator in its eigenbasis ${ |a_k \rangle }$. This will allow us to write $A = \sum_k |a_k \rangle \langle a_k|$. with each $a_k = b_k + i c_k$. Now write this as:

$$ \begin{aligned} & A = \sum_k (b_k + i c_k)|a_k \rangle \langle a_k| \ & A = \sum_k b_k |a_k \rangle \langle a_k| + i c_k |a_k \rangle \langle a_k| \ & A = B + iC \ \end{aligned} $$

$B, C$ are simultaneously diagonalizable in the eigenbasis ${ |a_k \rangle }$ and hence $[B, C] = 0$.

Readable pointers

I recently had to debug a whole bunch of code that manipuates pointers, so I need to stare at random things like 0x7f7d6ab2c0c0, like so:

mkClosure_capture0_args0 (0x7f079ae2a0c0:) -> 0x556b95a23350:
mkClosure_capture0_args0 (0x7f079ae2a0e0:) -> 0x556b95a3f3e0:
mkClosure_capture0_args2 (0x7f079ae2a000:, 
  0x556b95a23350:, 0x556b95a3f3e0:) -> 0x556b95a232e0:
evalClosure (0x556b95a232e0:)
  ⋮evalClosure (0x556b95a23350:)
  ⋮  ⋮mkConstructor1 (MkSimpleInt, 0x1) -> 0x556b9596c0b0:
  ⋮=>0x556b9596c0b0:
  ⋮isConstructorTagEq (0x556b9596c0b0:MkSimpleInt, MkSimpleInt) -> 1
  ⋮extractConstructorArg  0 -> 0x1:
  ⋮evalClosure (0x556b95a3f3e0:)
  ⋮  ⋮mkConstructor1 (MkSimpleInt, 0x2) -> 0x556b95a23190:
  ⋮=>0x556b95a23190:
  ⋮isConstructorTagEq (0x556b95a23190:MkSimpleInt, MkSimpleInt) -> 1
  ⋮extractConstructorArg  0 -> 0x2:
  ⋮mkConstructor1 (MkSimpleInt, 0x3) -> 0x556b95902a30:
=>0x556b95902a30:

I got annoyed because it's hard to spot differences across numbers. So I wrote a small '''algorithm''' that converts this into something pronounceable:

char *getPronouncableNum(size_t N) {
     const char *cs = "bcdfghjklmnpqrstvwxzy";
     const char *vs = "aeiou";

     size_t ncs = strlen(cs); size_t nvs = strlen(vs);

     char buf[1024]; char *out = buf;
     int i = 0;
     while(N > 0) {
         const size_t icur = N % (ncs * nvs);
         *out++ = cs[icur%ncs]; *out++ = vs[(icur/ncs) % nvs];
         N /= ncs*nvs;
         if (N > 0 && !(++i % 2)) { *out++ = '-'; }
     }
     *out = 0;
     return strdup(buf);
};

which gives me the much more pleasant output:

mkClosure_capture0_args0 (0x7fbf49b6d0c0:cisi-jece-xecu-yu) 
  -> 0x561c5f11f9d0:suje-zoni-ciho-ko
mkClosure_capture0_args0 (0x7fbf49b6d0e0:qosi-jece-xecu-yu) 
  -> 0x561c5f12f1b0:leda-guni-ciho-ko
mkClosure_capture0_args2 (0x7fbf49b6d000:ziqi-jece-xecu-yu, 
  0x561c5f11f9d0:suje-zoni-ciho-ko, 
  0x561c5f12f1b0:leda-guni-ciho-ko) 
    -> 0x561c5f11f960:kuhe-zoni-ciho-ko
evalClosure (0x561c5f11f960:kuhe-zoni-ciho-ko)
  ⋮evalClosure (0x561c5f11f9d0:suje-zoni-ciho-ko)
  ⋮  ⋮mkConstructor1 (MkSimpleInt, 0x1) -> 0x561c5f129c10:qifa-duni-ciho-ko
  ⋮=>0x561c5f129c10:qifa-duni-ciho-ko
  ⋮isConstructorTagEq (0x561c5f129c10:MkSimpleInt, MkSimpleInt) -> 1
  ⋮extractConstructorArg  0 -> 0x1:ca
  ⋮evalClosure (0x561c5f12f1b0:leda-guni-ciho-ko)
  ⋮  ⋮mkConstructor1 (MkSimpleInt, 0x2) -> 0x561c5f120200:nuhi-zoni-ciho-ko
  ⋮=>0x561c5f120200:nuhi-zoni-ciho-ko
  ⋮isConstructorTagEq (0x561c5f120200:MkSimpleInt, MkSimpleInt) -> 1
  ⋮extractConstructorArg  0 -> 0x2:da
  ⋮mkConstructor1 (MkSimpleInt, 0x3) -> 0x561c5f100010:kuqi-koni-ciho-ko
=>0x561c5f100010:kuqi-koni-ciho-ko

The strings of the form ziqi-jece-xecu-yu makes it way easier to see control flow. I can also see if two pointers are close, based on shared suffixes: ciho-ko is shared, which means the numbers are themselves close.

• It turns out there's a system called proquints that allows for such a thing already!

The grassmanian, handwavily

The grassmanian is a manifold consisting of, roughly, $k$ dimensional subspaces of an $n$ dimensional vector space.

Here, I'll record derivations of how we represent grassmanians, the exponential map, logarithm map, and the parallel transport with "physicist style" reasoning. Really, one needs to be careful because the grassmanian is a quotient of the non-compact steifel manifold, so we need to be careful about choosing representatives and whatnot. However, nothing beats physicist reasoning for intuition, so I'm going to do all the derivations in that style.

[WIP]

Lie bracket as linearization of conjugation

Let us have $Y = GXG^{-1}$ with all of these as matrices. Let's say that $G$ is very close to the identity: $G = I + E$ with $E^2 = 0$ ($E$ for epsilon). Note that now, $G^{-1} = (I + E)^{-1}$, which by abuse of notation can be written as $1/(I + E)$, which by taylor expansion is equal to $I - E + E^2 - E^3 + \dots$. Since $E$ is nilpotent, we truncate at $E^2$ leaving us with $(I - E)$ as the inverse of $(I+E)$. We can check that this is correct, by computing:

$$ \begin{aligned} &(I+E)(I - E) = \ &= I - E + E - E^2 \ &= I - E^2 = \ &= I - 0 = I \end{aligned} $$

This lets us expand out $Y$ as:

$$ \begin{aligned} &Y = GXG^{-1} \ &Y = (I + E)X(I + E)^{-1} \ &Y = (I + E)X(I - E) \ &Y = IXI -IXE + EXI - EXE \ &Y = X - XE + EX - EXE \end{aligned} $$

Now we assert that because $E$ is small, $EXE$ is of order $E^2$ and will therefore vanish. This leaves us with:

$$ GXG^{-1} = Y = X + [E, X] $$

and so the lie bracket is the Lie algebra's way of recording the effect of the group's conjugacy structure.

Computational Origami

• RabbitEar: library for building origami visualizations in the browser
• ORIPA: tool for visualizing flat folded origami
• TreeMaker:
• Origami Simulator: Tool to simulate origami, going from flat shaped to folded shaped

Katex in duktape

Here's some code to use duktape, a lightweight JavaScript interpreter to run katex when implementing a custom static site generator [as I am doing for this website]. This seems to be way more lightweight than relying on Node, since we don't need to pay for inter-procedure-calls.

I haven't benchmarked my static site generator against others, but I would be surprised if it is much faster, since it is written entirely in C, and avoids anything 'expensive'.

#include "duktape.h"
#include <stdio.h>
#include <assert.h>
typedef long long ll;

void vduk_print_stack(duk_context *ctx, const char *fmt, va_list args){
    char *outstr = nullptr;
    vasprintf(&outstr, fmt, args);
    assert(outstr);

    printf("\nvvv%svvv\n", outstr);
    printf("[TOP OF STACK]\n");
    const int len = duk_get_top(ctx);
    for(int i = 1; i <= len; ++i) {
        duk_dup(ctx, -i);
        printf("stk[-%2d] = %20s\n", i, duk_to_string(ctx, -1));
        duk_pop(ctx);
    }
    printf("^^^^^^^\n");
}


void duk_print_stack(duk_context *ctx, const char *fmt, ...) {
    va_list args;
    va_start(args, fmt);
    vduk_print_stack(ctx, fmt, args);
    va_end(args);
}
int main() {
    const char *latex_to_compile = "\\int_0^\\infty f(x) dx";
    const char *broken_latex_to_compile = "\\int_0^\\infty \\foobar f(x) dx";


    // FILE *fkatex = fopen("/home/bollu/blog/katex/katex.min.js", "rb");
    FILE *fkatex = fopen("/home/bollu/blog/katex/katex.min.js", "rb");
    if (fkatex == nullptr) { assert(false && "unable to open katex.min.js"); }

    fseek(fkatex, 0, SEEK_END);
    const ll len = ftell(fkatex); fseek(fkatex, 0, SEEK_SET);
    char *js = (char *)calloc(sizeof(char), len + 10);

    const ll nread = fread(js, 1, len, fkatex);
    assert(nread == len);
    duk_context *ctx = duk_create_heap_default();
    duk_push_string(ctx, "katex.min.js"); // for error message
    if (duk_pcompile_string_filename(ctx, 0, js) != 0) {
        fprintf(stderr, "===katex.min.js compliation failed===\n%s\n===\n", 
                duk_safe_to_string(ctx, -1));
        assert(false && "unable to compile katex.min.js");
    } else {
        fprintf(stderr, "===katex.min.js successfully complied===\n");

        duk_print_stack(ctx, "Stack afer compilation", __LINE__);
        duk_call(ctx, 0);   
        printf("program result: %s\n", duk_safe_to_string(ctx, -1));

    }



    // https://wiki.duktape.org/howtofunctioncalls
    duk_print_stack(ctx, "%d", __LINE__);
    if(duk_peval_string(ctx, "katex") != 0) {
        printf("eval failed: %s\n", duk_safe_to_string(ctx, -1));
        assert(0 && "unable to find the katex object");
    }  else {
        duk_print_stack(ctx, "%d", __LINE__);
    }

    duk_print_stack(ctx, "%d", __LINE__);
    duk_push_string(ctx, "renderToString");
    duk_push_string(ctx, latex_to_compile);

    duk_print_stack(ctx, "%d", __LINE__);
    if(duk_pcall_prop(ctx, -3, 1) == DUK_EXEC_SUCCESS) {
        printf("===katexed output:===\n%s\n", duk_to_string(ctx, -1));
    } else {
        printf("unable to katex: %s\n", duk_to_string(ctx, -1));
        assert(false && "unable to katex input");
    }
 
    return 0;
}

Kebab case

I learnt from the Nu shell blog that this-style-of-writing variables is called as kebab-case. Very evocative.

Localization: Introducing epsilons (WIP)

We can think of localization at a zero divisors as going from a regime of having divisors of zero into a regime of having $\epsilon$. I'll explore this perspective by consider $R = \mathbb Z/12 \mathbb Z$.

NaN punning

This is a technique that allows us to store data inside a double by punning the value of a NaN. This is used inside javascript engines to represent all possible user types as a single NaN. This is well explained at the SpiderMonkey internals page

#include <assert.h>
#include <iostream>
#include <limits>
using namespace std;
// https://en.wikipedia.org/wiki/NaN
union PunDouble { 
    double d;
    struct { 
        uint64_t m      : 51;
        uint32_t qnan: 1;
        uint32_t e      : 11;
        uint32_t s      : 1;
    } bits;
    PunDouble(double d) : d(d) {};
    PunDouble(uint32_t s, uint32_t e, uint64_t m) {
        bits.s = s;
        bits.e = e;
        bits.qnan = 1;
        bits.m = m;
    }
};

union PunInt {
    int32_t i;
    uint32_t bits;
    PunInt(int32_t i): i(i) {};
};

using namespace std;
struct Box {

    inline bool is_int() const { 
        auto pd = PunDouble(d);
        return pd.bits.e == 0b11111111111 && pd.bits.qnan == 1;
    }
    inline bool isdouble() const {
        auto pd = PunDouble(d);
        return (pd.bits.e != 0b11111111111) || (pd.bits.qnan == 0); 
    }
    int32_t get_int() const { 
        assert(is_int());
        uint64_t m = PunDouble(d).bits.m; return PunInt(m).i;
    }
    double get_double() const { assert(isdouble()); return d; }
    Box operator +(const Box &other) const;

    static Box mk_int(int32_t i) { 
        return Box(PunDouble(1, 0b11111111111, PunInt(i).bits).d);
    }
    static Box mk_double(double d) { return Box(d); }
    double rawdouble() const { return d; }
    private:
    double d; Box(double d) : d(d) {}
};

// = 64 bits
Box Box::operator + (const Box &other) const {
    if (isdouble()) { 
        assert(other.isdouble());
        return Box::mk_double(d + other.d);
    }
    else { 
        assert(is_int());
        assert(other.is_int());
        return Box::mk_int(get_int() + other.get_int());
    }
}

ostream &operator << (ostream &o, const Box &b) {
    if (b.isdouble()) { return o << "[" << b.get_double() << "]"; }
    else { return o << "[" << b.get_int() << "]"; }
}

int32_t randint() { return (rand() %2?1:-1) * (rand() % 100); }
                    
int32_t main() {

    // generate random integers, check that addition checks out
    srand(7);
    for(int32_t i = 0; i < 1000; ++i) {
        const int32_t i1 = randint(), i2 = randint();
        const Box b1 = Box::mk_int(i1), b2 = Box::mk_int(i2);
        cout << "i1:" << i1 << "  b1:" << b1 << "  b1.double:" << b1.rawdouble() << "  b1.get_int:" << b1.get_int() << "\n";
        cout << "i2:" << i2 << "  b2:" << b2 << "  b2.double:" << b2.rawdouble() << "  b2.get_int:" << b2.get_int() << "\n";
        assert(b1.is_int());
        assert(b2.is_int());
        assert(b1.get_int() == i1);
        assert(b2.get_int() == i2);
        Box b3 = b1 + b2;
        assert(b3.is_int());
        assert(b3.get_int() == i1 + i2);
    }

    for(int32_t i = 0; i < 1000; ++i) {
        const int32_t p1 = randint(), q1=randint(), p2 = randint(), q2=randint();
        const double d1 = (double)p1/(double)q1;
        const double d2 = (double)p2/(double)q2;
        const Box b1 = Box::mk_double(d1);
        const Box b2 = Box::mk_double(d2);
        cout << "d1: " << d1 << " | b1: " << b1 << "\n";
        cout << "d2 " << d2 << " | b2: " << b2 << "\n";
        assert(b1.isdouble());
        assert(b2.isdouble());

        assert(b1.get_double() == d1);
        assert(b2.get_double() == d2);;
        Box b3 = b1 + b2;
        assert(b3.isdouble());
        assert(b3.get_double() == d1 + d2);
    }
    return 0;
}

Offline Documentation

I'm collecting sources of offline documentation, because my internet has been quite unstable lately due to the monsoon. I realized that when it came to C, I would always man malloc, or apropos exit to recall the calloc API, or to learn about atexit. I wanted to get offline docs for all the languages I use, so I'm building a list:

• C: man pages
• C++: cppman
• C++: synth
• python: pydoc
• haskell: haddock

Using Gurobi

I've been trying to learn how to use Gurobi, the industrial strength solver for linear and quadratic equation systems.

• compile the C+ bindings

$ cd /path/to/gurobi90/linux64/src/build/ && make

osqp: convex optimizer in 6000 LoC

• Here's the github link to their repo

It's written by heavyweights like Boyd himself, the author of the famous convex optmization textbook and course.

╰─$ cloc .
     343 text files.
     329 unique files.
     163 files ignored.
---------------------
Language         code
---------------------
C                6483
C/C++ Header     3215
CMake            1930
make             1506
Python            701
C++               496
JSON              232
Markdown          213
Bourne Shell      186
DOS Batch         140
CSS               121
YAML              105
HTML               19
---------------------
SUM:            15347
---------------------

I find it amazing that all of the code lives in around 6500 lines. They're supposedly industrial strength, and can handle large problems. Reading this code should provide a lot of insight into how to write good convex optimizers! I would love to take a course which explains the source code.

stars and bars by generating functions

Say I have C colors of objects, and S slots to put these objects in. In how manys can I put objects into slots, without regard to order? For example, say we have 4 colors c, m, y, k and 2 slots _ _. The number of colorings that I want to count is:

cc cm cy ck
mc mm my mk
yc ym yy yk
kc km ky kk

Everything coloring on the lower diagonal (say, mc) is equivalent to one on the upper diagonal (cm). So in total, there are 10 colorings:

cc cm cy ck
*  mm my mk
*  *  yy yk
*  *  *  kk

One can solve this using stars-and-bars. Take the number of slots S to be the number of stars. Take the number of colors C to be the number of bars. The answer to the stars-and-basrs is the same as the coloring question.

I don't like stars and bars for this, because it seems to force an ordering of the colors c1 < c2 < .. < cn. [which bar cooresponds to which color]. Is there some way to not have to do this?

Is there some other way to show the (n + k - 1)Ck without imposing this ordering, or some other way to count this quantity?

One other way you can look at this is using multinomial expansion, but its computation is slightly more involved. Its advantage is that it ignores ordering of the objects, which is what you desire.

In this case, we represent each color as the polynomial 1 + x + x^2, here the power of x represents the number of instances you are taking of that color.

So, if you take (1 + x + x^2)^4, you have found the number of ways to arrange four colors, for different numbers of slots. If you take coefficient of x^2 from that polynomial, you get the answer to your question

Why does this set of shady manipulations not work?

answer = coeff. of x^2 in (1 + x + x^2)^4
[We can add higher powers, won't change coeff of x^2]
answer = coeff. of x^2 in (1 + x + x^2 + x^3)^4
answer = coeff. of x^2 in (1 + x + x^2 + ...)^4
answer = coeff. of x^2 in (1/(1-x))^4

Call f(x) = (1/(1-x))^4
f(x) =taylor= f(0) + f'(x) x + f''(0) x^2/2 + f'''(0) x^3 / 6 + ...

1/(1-x)^4 =taylor= ... + (1/(1-x)^4)''(0) x^2/2 + ...

so:

answer = coeff. of x^2 in ... + (1/(1-x)^4)''(0) x^2/2 + ...

Now compute (1/(1-x)^4)'' evaluated at 0 and divide by 2. This gives:

(1/(1-x)^4)'' (0)
= (-4/(1-x)^5)' (0)
= (20/(1-x)^6) (0)
= (20/(1-0)^6)
= (20)

so we get the answer as answer = 20/2! = 10.

This is not a place of honor

• Long term nuclear waste

Topological proof of infinitude of primes

We take the topological proof and try to view it from the topology as semidecidability perspective.

• Choose a basis for the topology as the basic open sets $S(a, b) = { a n + b : n \in \mathbb Z } = { mathbb Z + b }$. This set is indeed semi-decidable. Given a number $k$, I can check if $(k - b) % a == 0$. So this is our basic decidability test.
• By definition, $\emptyset$ is open, and $\mathbb Z = S(1, 0)$. Thus it is a valid basis for the topology. Generate a topology from this. So we are composing machines that can check in parallel if for some $i$, $(k - b[i]) % a[i] == 0$ for some index.
• The basis $S(a, b)$ is clopen, hence the theory is decidable.
• Every number other than the units ${+1, -1}$ is a multiple of a prime.
• Hence, $\mathbb Z \setminus { -1, +1 } = \cup_{p \text{prime}} S(p, 0)$.
• Since there a finite number of primes [for contradiction], the right hand side must be must be closed.
• The complement of $\mathbb Z \setminus { -1, +1 }$ is ${ -1, +1 }$. This set cannot be open, because it cannot be written as the union of sets of the form ${ a n + b }$: any such union would have infinitely many elements. Hence, $\mathbb Z \setminus { -1, +1 }$ cannot be closed.

Burnside Theorem

For a finite group $G$ acting on a set $X$, burnside's lemma equates (i) the number of equivalence classes of $X$ under $G$'s action, that is, the number of orbits of $X$ with (ii) the average number of stabilized elements for each $g \in G$. Formally, it asserts:

$$ |Orb(X, G)| = 1/|G|\sum_{g \in G} |Stab(g)| $$

As local/global principle

See that the right-hand-side measures "local fixed points" in terms of $|Stab(g)|$. The left hand side measures "global fixed points": an orbit $O \subseteq X$ is a set such that $G \cdot O = O$. So it's a sort of "global fixed point of $G$".

The burnside lemms tells us that we can recover the size of the set of global fixed points (the number of orbits) by averaging the size of the set of local fixed points (the average of the sizes of the stabilizers).

As space/time average

The left hand size is a time average: If we consider $X, GX, \dots G^{n}X$, we will finally be left with the images as the orbits. All other elements would have been ``smashed together''.

On the right hand side, we are averaging the group over space. Yes, but how does one perform averaging? One needs to have a measure!

A rephrasing in terms of integrators

Consider a system of a particle in a well. We consider two energy levels: that with E = 0, and E = 1. This gives us the following five states:

now I want to simulate this system, like a good computer scientist. So let's write the stupdiest one possible, Δ0, that doesn't simulate anything at all, and Δ+1, which steps the system forward by a single step. These look like this:

But why only these? Why privilege these time-scales? We should at least have Δ-1, for the arrow of time is fiction:

We should also have coarser integrators. Hence we contemplate Δ+2 and Δ-2. Turns out these are equivalent:

We can also consider Δ + 3. We also see that Δ + 4 = Δ:

So in conclusion, the calculation gives us:

The Ise Grand shrine

The shrine buildings at Naikū and Gekū, as well as the Uji Bridge, are rebuilt every 20 years as a part of the Shinto belief of the death and renewal of nature and the impermanence of all things and as a way of passing building techniques from one generation to the next.

I really enjoy this philosophy. I feel I should reflect on this, and update how I think about, say, code rewrites, and pouring billions into new supercolliders simply to keep the knowledge of how to build it alive.

The shrine has evolved throughout the years in its reconstruction, while maintaining some of its key features. The shrine was not originally constructed with gold copper adornments, however, because of advancements in technology as well as Buddhist influence, it gained them over the years.

Edward Kmett's list of useful math

• I use Bayesian statistics constantly for probabilistic programming and neural networks. Calculus gave me access to understand automatic differentiation, which gets used in everything I do. Real analysis doesn't come up often, but intermediate value thm. style arguments are handy.

• I don't use classic geometry, but I when I was doing graphics I used projective geometry, and that served as a gateway to understand category theory's duality principle, and I use category theory to organize most of the code I write.

• I took one course on differential geometry. The knowledge I gained from it probably led to about half of my income to date. I've made a career out of weaponizing "obscure" math, e.g. using toric varieties of rational functions of Zhegalkin polynomials to schedule instructions...

• Differential equations? Physics? Well, I use Hamiltonian methods for most of the sampling I do in the world of probabilistic programming. So understanding symplectic integrators is a big step, and I have to move frictionless particles subject to a Hamiltonian, so there's diff eq.

• Fourier analysis, heat equations? Well, if I want to approximate a space/distribution, http://ddg.math.uni-goettingen.de/pub/GeodesicsInHeat.pdf

• Learning group theory "bottom up" from monoids and the like has been useful, because I use monoids basically everywhere as a functional programmer to aggregate data. It led to the work I did at S&P Capital IQ, and later to basically my entire niche as a functional programmer.

• But understanding more of the surrounding landscape has been useful as well, as I use all sorts of lattices and order theory when working with propagators. And I use regular and inverse semigroups (note, not groups!) when working with all sorts of fast parsing techniques.

• Complex analysis? Understanding Moebius transformations means I can understand how continued fractions work, which leads to models for computable reals that don't waste computation and are optimally lazy. Knowing analytic functions lets me understand complex step differentiation.

• Linear algebra is in everything I've done since highschool. Learning a bit of geometric algebra, and playing around with Plucker coordinates led to me licensing tech to old game companies for computational visibility back before it was a "solved" problem.

• Wandering back a bit, Gröbner bases wind up being useful for comparing circuits modulo 'don't care' bits for impossible situations, and all sorts of other simplification tasks.

• Let's go obscure. Pade approximants? Good rational approximations, not polynomial ones. Sounds academic, but computing exp and log is expensive, and fast rational approximations can be conservative, monotone and have nice derivatives, speeding NN-like designs a lot.

• Weird number systems => Data structures. Category theory acts as a rosetta stone for so many other areas of math it isn't even funny. You can understand almost all of the essential bits of quantum computing just knowing by category theory.

• Logic. Well, which logic? You run into a modal logic in a philosophy class some time and think of it as a clever hack, but monads in FP are basically a modality. Modal logics for necessity/possibility model effect systems well. Substructural logics to manage resource usage...

• I don't use a lot of number theory. There. Mind you, this is also one of those areas where I'm just standing on weak foundations, so I don't know what I don't know. I just know it's hard to do all sorts of things that sound easy and try to muddle through w/ my limited background.

Cokernel is not sheafy

I wanted to understand why the Cokernel is not a sheafy condition. I found an explanation in Ravi Vakil's homework solutions which I am expanding on here.

Core idea

We will show that there will be an exact sequence which is surjective at each stalk, but not globally surjective. So, locally, we wil have trivial cokernel, but globally, we will have non-trivial cokernel.

Exponential sheaf sequence

$$ \begin{aligned} 0
\rightarrow 2\pi i \mathbb Z \xrightarrow{\alpha: \texttt{incl}} \mathfrak O \xrightarrow{\beta:exp(\cdot)} \mathfrak O^* \rightarrow 0 \end{aligned} $$

• $\mathfrak O$ is the sheaf of the additive group of holomorphic functions. $\mathfrak O^*$ is the sheaf of the group of non-zero holomorphic functions.
• $\alpha$, which embeds $2\pi n \in 2\pi i \mathbb Z$ as a constant function $f_n(\cdot) \equiv 2 \pi i n$ is injective.
• $\beta(\alpha(n)) = e^{2 \pi i n} = 1$. So we have that the composition of the two maps $\beta \circ \alpha$ is the zero map (multiplicative zero), mapping everything in $2\pi i \mathbb Z$ to the identity of $\mathfrak O^*$. Thus, d^2 = 0, ensuring that this is an exact sequence.
• Let us consider the local situation. At each point p, we want to show that $\beta$ is surjective. Pick any $g \in \mathfrak O^_p$. We have an open neighbourhood $U_g$ where $g \neq 0$, since continuous functions are locally invertible. Take the logarithm of $g$ to pull back $g \in O^_p$ to $\log g \in O_p$. Thus, $\beta: O \rightarrow O^p$ is surjective at each local point $p$, since every element has a preimage.
• On the other hand, the function $h(z) \equiv z$ cannot be in $O^*$ If it were, then there exists a homolorphic function called $l \in O$ [for $\log$] such that $\exp(l(z)) = h(z) = z$ everywhere on the complex plane.
• Assume such a function exists. Then it must be the case that $d/dz exp(l(z)) = d/dz(z) = 1$. Thus, $exp(l(z)) l'(z) = z l'(z) = 1$ [use the fact that $exp(l(z)) = z$]. This means that $l'(z) = 1/z$.
• Now, by integrating in a closed loop of $e^{i \theta}$. we have $\oint l'(z) = l(1) - l(1) = 0$.
• We also have that $\oint l'(z) = \oint 1/z = 2\pi i$.
• This implies that $0 = 2\pi i$ which is absurd.
• Hence, we cannot have a function whose exponential gives $h(z) = z$ everywhere.
• Thus, the cokernel is nontrivial globally.

Von neumann: foundations of QM

• I wanted to understand what von neumann actually did when he "made QM rigorous", what was missing, and why we need $C^\star$ algebras for quantum mechanics, or even "rigged hilbert spaces".
• I decided to read Von Neumann: Mathematical foundations of quantum mechanics.
• It seems he provides a rigorous footing for QM, without any dirac deltas. In particular, he proves the Reisez representation theorem, allow for transforming bras to kets and vice versa. On the other hand, it does not allow for dirac delta as bras and kets.
• The document The role of rigged hilbert spaces in QM provides a gentle introduction on how to add in dirac deltas.
• Rigged hilbert spaces (by Gelfand) combine the theory of distributions (by Schwartz), developed to make dirac deltas formal, and the theory of hilbert spaces (by Von Neumann) developed to make quantum mechanics formal.
• To be even more abstract, we can move to $C^\star$ algebras, which allow us to make QFT rigorous.
• So it seems that in total, to be able to write, say, a "rigorous shankar" textbook, one should follow Chapter 2 of Von Neumann, continuing with the next document which lays out how to rig a hilbert space.
• At this point, one has enough mathematical machinery to mathematize all of Shankar.

References

• Von neumann: Mathematical foundations of quantum mechanics.
• The role of rigged hilbert spaces in QM

Discrete schild's ladder

If one is given a finite graph $(V, E)$, which we are guaranteed came from discretizing a grid, can we recover a global sense of orientation?

• More formally, assume the grid was of dimensions $W \times H$. So we have the vertex set as $V \equiv { (w, h) 1 \leq w \leq W, 1 \leq h \leq H }$. We have in the edge set all elements of the form $((w, h), (w \pm 1, h \pm 1))$ as long as respective elements $(w, h)$ and $(w \pm 1, h \pm 1)$ belong to $V$.

• We lose the information about the grid as comprising of elements of the form $(w, h)$. That is, we are no longer allowed to "look inside". All we have is a pile of vertices and edges $V, E$.

• Can we somehow "re-label" the edges $e \in E$ as "north", "south", "east", and "west" to regain a sense of orientation?

• Yes. Start with some corner. Such a corner vertex will have degree 2. Now, walk "along the edge", by going from a vertex of degree 2 to an neighbour of degree 2. If we finally reach a vertex that has unexplored neighbours of degree 3 or 4, pick the neighbour of degree 3. This will give us "some edge" of the original rectangle.

• We now arbitrary declare this edge to be the North-South edge. We now need to build the perpendicular East-West edge.

• This entire construction is very reminisecent of Schild's Ladder

Derivative of step is dirac delta

I learnt of the "distributional derivative" today from my friend, Mahathi. Recording this here.

The theory of distributions

As far as I understand, in the theory of distributions, A distribution is simply a linear functional $F: (\mathbb R \rightarrow \mathbb R) \rightarrow \mathbb R$. The two distributions we will focus on today are:

• The step distribution, $step(f) \equiv \int_0^\infty f(x) dx$
• The dirac delta distribution, $\delta(f) = f(0)$.
• Notationally, we write $D(f)$ where $D$ is a distribution, $f$ is a function as $\int D(x) f(x) dx$.
• We can regard any function as a distribution, by sending $f$ to $F(g) \equiv \int f(x) g(x) dx$.
• But it also lets us cook up "functions" like the dirac delta which cannot actually exist as a function. So we move to the wider world of distributions

Derivative of a distribution

Recall that notationally, we wrote $D(f)$ as $\int D(x)f(x) dx$. We now want a good definition of the derivative of the distribution, $D'$. How? well, use chain rule!

$$ \begin{aligned} &\int_0^\infty U dV = [UV]|_0^\infty - \int_0^\infty V dU \ &\int_0^\infty f(x) D'(x) dx \ &= [f(x) D(x)]|_0^\infty - \int_0^\infty D f'(x) \end{aligned} $$

Here, we assume that $f(\infty) = 0$, ahd that $f$ is differentiable at $0$. This is because we only allow ourselves to feed into these distribtions certain classes of functions (test functions), which are "nice". The test functions $f$ (a) decay at infinity, and (b) are smooth.

The derivation is:

$$ \begin{aligned} &\int_0^\infty U dV = \int_0^\infty f(x) \delta(x) = f(0) \ &[UV]|_0^\infty - \int_0^\infty V dU = [f(x) step(x)]|_0^\infty - \int_0^\infty step(x) f'(x) \ &= [f(\infty)step(\infty) - f(0)step(0)] - step(f') \ &= [0 - 0] - (\int_0^\infty f'(x) dx) \ &= 0 - (f(\infty) - f(0)) \ &= 0 - (0 - f(0)) \ &= f(0) \end{aligned} $$

• Thus, the derivative of the step distribution is the dirac delta distribution.

Extended euclidian algorithm

Original definition

I feel like I only understand the extended euclidian algorithm algebraically, so I've been trying to understand it from other perspectives. Note that we want to find $gcd(p, p')$. WLOG, we assume that $p > p'$. We now find a coefficient $d$ such that $p = d p' + r$ where $0 \leq r < p'$. At this stage, we need to repeat the algorithm to find $gcd(p', r)$. We stop with the base case $gcd(p', 0) = p'$.

My choice of notation

I dislike the differentiation that occurs between $p$, $p'$, and $r$ in the notation. I will notate this as $gcd(p_0, p_1)$. WLOG, assume that $p_0 > p_1$. We now find a coefficient $d_0$ such that $p_0 = p_1 d_1 + p_2$ such that $0 \leq p_2 < p_1$. At this stage, we recurse to find $gcd(p_1, p_2)$. We stop with the base case $gcd(p_{n-1}, p_n) = p_n$ iff $p_{n-1} = d_n p_n + 0$. That is, when we have $p_{n+1} = 0$, we stop with the process, taking the gcd to be $p_n$.

Matrices

We can write the equation $p_0 = p_1 d_1 + p_2$ as the equation $p_0 = [d_1; 1] [p_1; p_2]^T$. But now, we have lost some state. We used to have both $p_1$ and $p_2$, but we are left with $p_0$. We should always strive to have "matching" inputs and output so we can iterate maps. This leads us to the natural generalization:

$$ \begin{bmatrix} p_0 \ p_1 \end{bmatrix} = \begin{bmatrix} d_1 & 1 \ 1 & 0 \end{bmatrix} \begin{bmatrix} p_1 \ p_2 \end{bmatrix} $$

So at the first step, we are trying to find a $(d_1, p_2)$ such that the matrix equation holds, and $0 \leq p_2 < d_1$.

Extended euclidian division

When we finish, we have that $gcd(p_{n-1}, p_n) = p_n$. I'll call the GCD as $g$ for clarity. We can now write the GCD as a linear combination of the inputs $g = p_n = 0 \cdot p_{n-1} + 1 \cdot p_n$. We now want to backtrack to find out how to write $g = \omega_{n-2} p_{n-2} + \omega_{n-1} p_{n-1}$. And so on, all the way to $g = \omega_0 p_0 + \omega_1 p_1$.

• We can begin with the general case:

$$ g = \begin{bmatrix} \omega' & \omega'' \end{bmatrix} \begin{bmatrix} p' \ p'' \end{bmatrix} $$

• We have the relationship:

$$ \begin{bmatrix} p \ p' \end{bmatrix} = \begin{bmatrix} d' & 1 \ 1 & 0 \end{bmatrix} \begin{bmatrix} p' \ p'' \end{bmatrix} $$

• We can invert the matrix to get:

$$ \begin{bmatrix} p' \ p'' \end{bmatrix} = \begin{bmatrix} 0 & 1 \ 1 & - d' \end{bmatrix} \begin{bmatrix} p \ p' \end{bmatrix} $$

• now combine with the previous equation to get:

$$ \begin{aligned} &g = \begin{bmatrix} \omega' & \omega'' \end{bmatrix} \begin{bmatrix} p' \ p'' \end{bmatrix} \ &g = \begin{bmatrix} \omega' & \omega'' \end{bmatrix} \begin{bmatrix} 0 & 1 \ 1 & - d' \end{bmatrix} \begin{bmatrix} p \ p' \end{bmatrix} \ &g = \begin{bmatrix} \omega'' & \omega - d' \omega' \end{bmatrix} \begin{bmatrix} p \ p' \end{bmatrix} \

\end{aligned} $$

Fractions

• GCD factorization equation: $p/p' = (\alpha p' + p'')/p' = \alpha + p''/p'$.
• Bezout equation: $\omega' p' + \omega'' p'' = g$.
• Bezout equation as fractions $\omega' + \omega'' p''/p' = g/p'$.

In a PID, all prime ideals are maximal, geometrically

Assume $R$ is Noetherian.

• By Krull's principal ideal theorem, we have that given a principal ideal $I = (\alpha)$, all minimal prime ideals $\mathfrak p$ above $I$ has height at most 1.

• Recall that a minimal prime ideal $\mathfrak p$ lying over an ideal $I$ is the minimal among all prime ideals containing $I$. That is, if $I \subseteq \mathfrak q \subseteq \mathfrak p$, then $\mathfrak q = I$ or $\mathfrak q= \mathfrak p$.

• In our case, we have that $R$ is a PID. We are trying to show that all prime ideals are maximal. Consider a prime ideal $\mathfrak p \subseteq R$. It is a principal ideal since $R$ is a PID. It is also a minimal prime ideal since it contains itself. Thus by Krull's PID theorem, has height at most one.

• If the prime ideal is the zero ideal ($\mathfrak p = 0$), then it has height zero.

• If it is any other prime ideal $(\mathfrak p \neq (0))$, then it has height at least 1, since there is the chain $(0) \subsetneq \mathfrak p$. Thus by Krull's PID theorem, it has height exactly one.

• So all the prime ideals other than the zero ideal, that is, all the points of $Spec(R)$ have height 1.

• Thus, every point of $Spec(R)$ is maximal, as there are no "higher points" that cover them.

• Hence, in a PID, every prime ideal is maximal.

In a drawing, it would look like this:

NO IDEALS ABOVE  : height 2
(p0)  (p1) (p2)  : height 1
      (0)        : height 0

So each pi is maximal.

This is a geometric way of noting that in a principal ideal domain, prime ideals are maximal.

References

• Andreas Gathmann's notes

Prime numbers as maximal among principal ideals

I learnt of this characterization from benedict gross's lectures, lecture 31.

We usually define a number $p \in R$ as prime iff the ideal generated by $p$, $(p)$ is prime. Formally, for all $a, b \in R$, if $ab \in (p)$ then $a \in (p)$ or $b \in (p)$.

This can be thought of as saying that among all principal ideals, the ideal $(p)$ is maximal: no other principal ideal $(a)$ contains it.

Element based proof

• So we are saying that if $(p) \subseteq (a)$ then either $(p) = (a)$
• Since $(p) \subseteq (a)$ we can write $p = ar$. Since $(p)$ is prime, and $ar = p \in (p)$, we have that either $a \in (p) \lor r \in (p)$.
• Case 1: If $a \in (p)$ then we get $(a) \subseteq (p)$. This gives $(a) \subseteq (p) \subseteq (a)$, or $(a) = (p)$.
• Case 2: Hence, we assume $a \not \in (p)$, and $r \in (p)$. Since $r \in (p)$, we can write $r = r'p$ for some $r' \in R$. This gives us $p = ar$ and $p = a(r'p)$. Hence $ar' = 1$. Thus $a$ is a unit, therefore $(a) = R$.

Axiom of Choice and Zorn's Lemma

I have not seen this "style" of proof before of AoC/Zorn's lemma by thinking of partial functions $(A \rightarrow B)$ as monotone functions
on $(A \cup \bot \rightarrow B)$.

Zorn's Lemma implies Axiom of Choice

If we are given Zorn's lemma and the set $A_i$, to build a choice function, we consider the collection of functions $(f: \prod_i A_i \rightarrow \rightarrow A_i \cup \bot)$ such that either $f(A_i) = \bot$ or $f(A_i) \in A_i$. This can be endowed with a partial order / join semilattice structure using the "flat" lattice, where $\bot < x$ for all $x$, and $\bot \sqcup x = x$.

For every chain of functions, we have a least upper bound, since a chain of functions is basically a collection of functions $f_i$ where each function $f_{i+1}$ is "more defined" than $f_i$.

Hence we can always get a maximal element $F$, which has a value defined at each $F(A_i)$. Otherwise, if we have $F(A_i) = \bot$, the element is not maximal, since it is dominated by a larger function which is defined at $A_i$.

Hence, we've constructed a choice function by applying Zorn's Lemma. Thus, Zorn's Lemma implies Axiom of Choice.

Local ring in terms of invertibility

Recall that a local ring $R$ is a ring with a unique maximal ideal $M$. This is supposedly equivalent to the definition:

A local ring is a ring $R$ such that $1 \neq 0$ and for all $x, y$ in $R$, $x + y \text{ invertible} \implies x \text{ invertible} \lor y \text{ invertible}$

Stepping stone: If $(R, M)$ is a local ring then set of all units of $R$ is equal to $R - M$

All elements of $(R - M)$ are units:

• Let $R$ be a local ring with unique maximal ideal $M$.
• Let $u \in R - M$. [$u$ for unit].
• If $u$ is a unit, we are done.
• Otherwise, consider the ideal generated by $u$, $(u)$.
• $(u)$ must live in some maximal ideal. Since
• $M$ is the only maximal ideal, we have that $u \in (u) \subseteq M$.
• This is a contradiction, since $u$ cannot be both in $M$ and $R - M$.
• Hence all elements $u \in R - M$ are units.

All units are in $(R - M)$:

• Let $u$ a unit.
• We cannot have $u \in M$ since $M$ is a maximal ideal, $M \neq R$.
• If $u \in M$ then $u^{-1} u = 1 \in M$, hence $M = R$.
• Contradiction.

Part 1: Local ring to to invertible:

• Let $R$ have a unique maximal ideal $M$.
• We have already shown that all invertible elements are in $R - M$.
• Hence if $x + y$ is invertible, it belongs to $R - M$.
• We must have either $x$ or $y$ invertible.
• Suppose not: $x, y \in M$ while $x + y \not \in M$.
• This is impossible because $M$ is an ideal and is thus closed under addition.
• So, we must have that if $x + y$ is invertible then either $x$ or $y$ is invertible.

Part 2: Invertible to Local ring.

• Let $R$ be a ring such that if $x + y$ is invertible then either $x$ or $y$ is invertible.
• Conversely, if neither $x$ nor $y$ are invertible then $x + y$ is not invertible.
• Hence the set of non-invertible elements form an ideal $I$, as $0 \in I$, sum of non-invertibles are not invertible (assumption), product of non-invertibles is not invertible (easy proof).
• This ideal $I$ is contained in some maximal ideal $M$.
• This maximal ideal $M$ is such that every element in $R - M$ is invertible, since all the non-invertible elements were in $I$ from which $M$ was built.
• Formally, assume not: Some element $s \in R - M$ is not invertible. Then $s \in I \subseteq M$. This contradicts assumption that $s \in R - M$.
• Hence $M$ is a unique maximal ideal and $R$ is a local ring.

References

• Using the internal language of toposes in algebraic geometry

Nullstellensatz for schemes

System of equations

Consider a set of polynomials ${F_1, F_2, \dots F_m}$ subset $K[T_1, \dots, T_n]$. A system of equations $X$ for unknowns $T$ is the tuple $(K[T_1, \dots, T_n], { F_1, F_2, \dots F_m } \subset K[T_1, \dots, T_n])$. We abbreviate this to $(K[\mathbf T], \mathbf F)$ where the bolded version implies that these are vectors of values.

Solutions to system of equations

Note that we often define equations, for example $x^2 + 1 = 0$ over a ring such as $\mathbb Z$. But its solutions live elsewhere: In this case, the solutions live in $\mathbb C$, as well as in $\mathbb Z/2Z$. Hence, we should not restrict our solution space to be the ring where we defined our coefficients from!

Rather, as long as we are able to interpret the polynomial $f \in K[\mathbf T]$ in some other ring $A$, we can look for solutions in the ring $A$. Some thought will tell us that all we need is a ring homomorphism $\phi: K \rightarrow L$. Alternatively/equivalently, we need $L$ to be a $K$-algebra.

Let us consider the single-variable case with $K[T]$. This naturally extends to the multivariate case. Using $\phi$, we can map $f \in K[T]$ to $\phi(f) \in L[T]$ by taking $f = \sum_i k_i T^i$ to $\phi(f) = \sum_i \phi(k_i) T^i$. This clearly extends to the multivariate case. Thus, we can interpret solutions $l \in L$ to an equation $f \in K[T]$ as $f(l) = \sum_i \phi(k_i) l^i$.

Formally, the solution to a system $X \equiv (K[\mathbf T], \mathbf F)$ in ring $L$, written as $Sol(X, L)$ is a set of elements $ls \subseteq L$ such that $F_i(l) = 0$ for all $l$ in $ls$ and for all $F_i$ in $\mathbf F$.

Equivalent systems of equations

Two systems of equations $X, Y$ over the same ring $K$ are said to be equivalent over $K$ iff for all $K$-algebras $L$, we have $Sol(X, L) = Sol(Y, L)$.

Biggest system of equations

For a given system of equations $X \equiv (K[\mathbf T], \mathbf F)$ over the ring $K$, we can generate the largest system of equations that still has the same solution: generate the ideal $\mathbf F' = (\mathbf F)$, and consider the system of equations $X' \equiv (K[\mathbf T], \mathbf F' = (\mathbf F) )$.

Varieties and coordinate rings

Let $g \in K[T_1, \dots T_n]$. The polynomial is also a function which maps $\mathbf x \in K^n$ to $K$ through evaluation $g(\mathbf x)$.

Let us have a variety $V \subseteq k^n$ defined by some set of polynomials $\mathbf F \in K[T_1, \dots, T_n]$. So the variety is the vanishing set of $\mathbf F$, and $\mathbf F$ is the largest such set of polynomials.

Now, two functions $g, h \in K[T_1, \dots, T_n]$ are equal on the variety $V$ iff they differ by a function $z$ whose value is zero on the variety $V$. Said differently, we have that $g|V = h|V$ iff $h - g = z$ where $z$ vanishes on $V$. We know that the polynomials in $\mathbf F$ vanish on $V$, and is the largest set to do so. Hence we have that $z \in \mathbf F$.

To wrap up, we have that two functions $g, h$ are equal on $V$, that is, $g|V = h|V$ iff $g - h \in \mathbf F$.

So we can choose to build a ring where $g, h$ are "the same function". We do this by considering the ring $K[V] \equiv K[T_1, \dots, T_n] / \mathbf F$. This ring $K[V]$ is called as the coordinate ring of the variety $V$.

An aside: why is it called the "coordinate ring"?

We can consider the ith coordinate function as one that takes $K[T_1, \dots, T_n]$ to $T_i$ So we have $\phi_i \equiv T_i \in K[T_1, \dots, T_n]$ which defines a function $\phi_i: K^n \rightarrow K$ which extracts the $i$th coordinate.

Now the quotienting from the variety to build $K[V]$, the coordinate ring of the variety $V$ will make sure to "modulo out" the coordinates that "do not matter" on the variety.

Notation for coordinate ring of solutions: $Coord(X)$

For a system $X \equiv (K[\mathbf T], \mathbf F)$, we are interested in the solutions to $\mathbf F$, which forms a variety $V(\mathbf F)$. Furthermore, we are interested in the algebra of this variety, so we wish to talk about the coordinate ring $k[V(\mathbf F)] = K[\mathbf T] / (\mathbf F)$. We will denote the ring $k[\mathbf T] / (\mathbf F)$ as $Coord(X)$.

Solutions for $X$ in $L$: $K$-algebra morphisms $Coord(X) \rightarrow L$

Let's simplify to the single variable case. Multivariate follows similarly by recursing on the single variable case. $X \equiv (K[T], \mathbf F \subseteq K[T])$.

There is a one-to-one coorespondence between solutions to $X$ in $L$ and elements in $Hom_K(Coord(X), L)$ where $Hom_K$ is the set of $K$-algebra morphisms.

Expanding definitions, we need to establish a correspondence between

• Points $l \in L$ such that $eval_l(f) = 0$ for all $f \in F$.
• Morphisms $K[T] / (\mathbf F) \rightarrow L$.

Forward: Solution to morphism

A solution for $X$ in $L$ is a point $\mathbf l \in L$ such that $F$ vanishes on $l$. Thus, the evaluation map $eval[l]: K[T] \rightarrow L$ has kernel $(\mathbf F)$. Hence, $eval[l]$ forms an honest to god morphism between $K[T] / (\mathbf F)$ and $L$.

Backward: morphism to solution

Assume we are given a morphism $\phi: Coord(X) \rightarrow L$. Expanding definitions, this means that $\phi: K[T]/ (\mathbf F) \rightarrow L$. We need to build a solution. We build the solution $l\star = \phi(T)$.

Intuitively, we are thinking of $\phi$ as $eval[l\star]$. If we had an $eval[l\star]$, then we would learn the point $l\star \in L$ by looking at $evall\star$, since $evall\star = l\star$.

We can show that this point exists in the solution as follows: $$ \begin{aligned} &evall\star = \sum_i a_i (l\star)^i \ &= \sum_i a_i \phi(T)^i \ &\text{Since $\phi$ is ring homomorphism:} \ &= \sum_i a_i \phi(T^i) \ &\text{Since $\phi$ is $k$-algebra homomorphism:} \ &= \phi(\sum_i a_i T^i) \ &= \phi(f) \ \text{Since $f \in ker(\phi)$:} \ &= 0 \end{aligned} $$

• This is also asked by me on this math.se question

Consistent and inconsistent system $X$ over ring $L$

Fix a $K$-algebra $L$. The system $X$ is consistent over $L$ iff $Sol(X, L) \neq \emptyset$. the system $X$ over $L$ is inconsistent iff If $Sol(X, L) = \emptyset$.

Geometric Language: Points

Let $K$ be the main ring, $X \equiv (K[T_1, \dots T_n], \mathbf F)$ a system of equations in $n$ unknowns $T_1, \dots, T_n$.

For any $K$-algebra $L$, we consider the set $Sol(X, L)$ as a collection of points in $L^n$. These points are solutions to the system $X$.

The points of $K$-algebra

References

• Manin, theory of schemes
• Notes coordinate rings of affine varieties
• Why is this called the coordinate ring

Perspectives on Yoneda

We can try to gain intuition for Yoneda by considering a finite category where we view arrows as directed paths.

The "interpretation" of a path is taken by going from edges to labels and then concatenating all edge labels. We "interpret" the label id_x as "" (the empty string), and we "interpret" all other arrows a as some unique string associated to each arrow. Composition of arrows becomes concatenation of strings. This obeys all the axioms of a category. We are basically of a category as a free monoid.

Let's being our consideration of the covariant functor Hom(O, -): C → Set. Note that the objects of this category are sets of arrows Hom(O, P). To every arrow a: P → Q we associate the set function a': Hom(O, P) → Hom(O, Q). a'(op) = pq . op.

Now, to apply Yoneda, we need another covariant functor G: S → Set. We now need to show that the set of natural transformations η: F → G are in bijection with the set G[O] ∈ Set.

We do this by the following consideration. Recall that for the natural transformation, we have the commuting diagram:

x -p-> y

Hom(o, x) -p'-> Hom(o, y)
|                |
ηx               ηy
|                |
v                v
G[x] -G[p] --> G[y]

∀ x y ∈ C,
  o2x ∈ Hom(o, x),
  p ∈ Hom(x, y),
    G[p](ηx(o2x)) = ηy(p'(o2x))

Which on using the definition of p' becomes:

∀ x y ∈ C,
  o2x ∈ Hom(o, x),
  p ∈ Hom(x, y),
  G[p](ηx(o2x)) = ηy(o2x . p')

Now pick the magic x = o and o2x = o2o = id_o. This gives:

x = o, y ∈ C
o2x = id_o

∀ y ∈ C, 
  p ∈ Hom(o, y),
  G[p](ηo(id_o)) = ηy(id_o . p')
  G[p](ηo(id_o)) = ηy(p') [By identity arrow]
  [assume we fix ηo(id_o) ∈ G[o] ]
  ηy(p') = G[p](ηo(id_o)) [ηy is now forced.
                          everything on the RHS is known]

Hence, we learn how to map every other arrow ηy(p). If we know how to map the arrows, we can map the objects in the hom-sets as images of the arrows, since we know what ηo[id_o] maps to. Concretely:

Images ηo(q) for q ∈ Hom(o, o) after ηo(id_o) is fixed:

We have the relation id_o . q = q. So we get that the arrow q': Hom(o, o) → Hom(o, o) takes id_o to q. By the structure of the natural transformation, we have that:

∀ x y ∈ C,
  o2x ∈ Hom(o, x),
  p ∈ Hom(x, y),
    G[p](ηx(o2x)) = ηy(p'(o2x))

• Pick x = y = o, o2x = id_o, p = q. This gives:

    G[q](ηo(id_o)) = ηo(q'(id_o))
    G[q](ηo(id_o)) = ηo(q' . id_o)
    G[q](ηo(id_o)) = ηo(q')
    ηo(q') = G[q](ηo(id_o))

Hence, we've deduced ηo(q'), so we know what element q gets mapped to. The same process works with any arrow!

A shift in perspective: Yoneda as partial monoid.

Since we're considering the sets $Hom(o, -)$, note that we can always pre-compose any element of $Hom(o, o)$ to every $Hom(o, p)$. More-over, if we know the value of $id_o$, then we have the equation that $id_o \circ a = a$. since $id_o$ is the identity. Moreover, $id_o$ is the only identity arrow we possess across all $Hom(o, -)$: We can only access the identity arrow inside $Hom(o, o)$. For all other $Hom(o, p)$ where $p \neq o$, we do not have the identity arrow $id_o$ or $id_p$. So we have a sort of partial monoid, where we have a unique identity element $id_o$, and arrows that compose partially based on domain/codomain conditions.

From this perspective, we can read the commutative diagram laws as a sort of "Cayley's theorem". We have as elements the elements of the set $Hom(o, -)$. For every arrow $a: p \rightarrow q$, we have the action $Hom(o, p) \xrightarrow{a} Hom(o, q)$.

From this perspective, it is trivial to see that:

• Every monoid can be embedded into its action space (Cayley's theorem).
• This mapping of yoneda from $Hom(o, -)$ to arbitrary sets is like a "forgetful" functor from a monoid into a semigroup.
• If our monoid is "well represented" by a semigroup, then once we know what the identity maps to, we can discover all of the other elements by using the relation $f(ex) = f(e) f(x)$. The only "arbitrariness" introduced by forgetting the monoid structure is the loss of the unique identity. NOTE: This is handwavy, since the data given by a natural transformation is somehow "different", in a way that I'm not sure how to make precise.

Germs, Stalks, Sheaves of differentiable functions

I know some differential geometry, so I'll be casting sheaves in terms of tangent spaces for my own benefit

• Presheaf: Data about restricting functions.
• Germ: Equivalence class of functions in the neighbourhood at a point, which become equivalent on restriction. Example: equivalence classes of curves with the same directional derivative.
• Stalk: An algebraic object worth of germs at a point.

Next, to be able to combine germs together, we need more.

• Sheaf: Adds data to a presheaf to glue functions.

A presheaf that is not a sheaf: Bounded functions

Consider the function $f(x) \equiv x$. This is bounded on every open interval $I \equiv (l, r)$: $l \leq f(I) \leq f(r)$ But the full function $f(x)$ is unbounded.

Holomorphic function with holomorphic square root.

Our old enemy, monodromy shows up here. Consider the identity function $f(z) = z$. Let's analyze its square root on the unit circle. $f(e^{i \theta}) = e^{i \theta/2}$. This can only be defined continuously for half the circle. As we go from $\theta: 0 \rightarrow 2 \pi$, our $z$ goes from $0 \rightarrow 0$, while $f(z)$ goes $0 \rightarrow -1$. This gives us a discontinuity at $0$.

Formalisms

• Sections of a presheaf $F$ over an open set $U$: For each open set $U \subseteq X$, we have a set $F(U)$, which are generally sets of functions. The elements of $F(U)$ are called as the Sections of $F$ over $U$. More formally, we have a function $F: \tau \rightarrow (\tau \rightarrow R)$ $(\tau \rightarrow R)$ is the space of functions over $\tau$.
• Restriction Map: For each inclusion $U \hookrightarrow V$, ($U \subseteq V$) we have a restriction map $Res(V, U): F(V) \rightarrow F(U)$.
• Identity Restriction: The map $Res(U, U)$ is the identity map.
• Restrictions Compose: If we have $U \subseteq V \subseteq W$, we must have $Res(W, U) = Res(W, V) \circ Res(V, U)$.
• Germ: A germ of a point $p$ is any section over any open set $U$ containing $p$. That is, the set of all germs of $p$ is formally $Germs(p) \equiv { F(U_p) : U_p \subseteq X, p \in U, U \text{ open} }$. We sometimes write the above set as $Germs(p) \equiv { (f, U_p) : f \in F(U_p), U_p \subseteq X, p \in U, U \text{ open} }$. This way, we know both the function $f$ and the open set $U$ over which it is defined.
• Stalk: A stalk at a point $p$, denoted as $F_p$, consists of equivalence classes of all germs at a point, where two germs are equivalent if the germs become equal over a small enough set. We state that $(f, U) \sim (g, V)$ iff there exists a $W \subseteq U \cap V$ such that the functions $f$ and $g$ agree on $W$: $Res(U, W)(f) = Res(V, W)(g)$.
• Stalk as Colimit: We can also define the stalk as a colimit. We take the index category $J$ as a filtered set. Given any two open sets $U, V$, we have a smaller open set that is contained in $U \cap V$. This is because both $U$ and $V$ cannot be non-empty since they share the point $p$.
• If $p \in U$ and $f \in F(U)$, then the image of $f$ in $F_p$, as in, the value that corresponds to $f$ in the stalk is called as the germ of $f$ at $p$. This is really confusing! What does this mean? I asked on math.se.

References

• The rising sea by Ravi Vakil.

Connectedness in terms of continuity

This was a shower thought.

• We usually define a topological space $X$ as connected iff there are disjoint open sets $U, V$ such that $U \cup V = X$. Since they are disjoint, we have that $U \cap V = \emptyset$.
• An alternative way of stating this is to consider two colors C = {red, blue } with the discrete topology.
• We use the discrete topology on C since we want the two colors to be "separate".
• Now, a space $X$ is connected iff there is a continuous surjective function $f: X \rightarrow C$. That is, we can color the whole space continuously with both colors.

This is equivalent to the original definition by setting $U = f^{-1}(red)$ and $V = f^{-1}(blue)$:

• Pre-images of a function must be disjoint. Hence, $U \cap V = \emptyset$.
• Preimages of $red$ and $blue$ must be open sets since ${red}$ and ${blue}$ are open and $f$ is continuous: continuous functions have pre-images of open sets as open. Hence $U$ and $V$ are open.
• Since $f$ is surjective, we must have that the pre-images cover the entire set $X$. Hence $U \cup V = X$.

I find this to be appealing, since it's intuitively obvious to me that if a space is disconnected, I can color it continuously with two colors, while if a space is connected, I should be unable to color it continuously with two colors --- there should be a point of "breakage" where we suddenly switch colors.

Intuition for limits in category theory

A characterization of limits

The theorem that characterizes limits is this:

A category has Finite Limits iff it has all finite products and equalizers. limits have maps out of them.

Ravi Vakil's intuition for limits: Take sub things.

• An element of a limit gives one of each of its ingredients. For example, $K[[X]] = \lim_n \text{degree}n\text{polynomials} $, since we can get a degree n polynomial for all n, from any power series by truncation.
• limits have maps out of them.
• RAPL: right adjoints preserve limits.
• Limits commute with limits.
• These are mentioned in "Algebraic geometry in the time of Covid: Pseudolecture 2"
• Also, recalling that kernels are limits allows one to remember that we have maps that go out of a limit.

Limits are things you get maps out of.

• product has projections going out of it.
• gcd is less than the things that build it: gdb(a, b) -> a, b since gcd(a, b) < a and gcd(a, b) < b.
• single point set can be mapped out of.
• type Limit f = forall a. f a

Limits in Haskell

{-# LANGUAGE ExplicitForAll #-}
{-# LANGUAGE RankNTypes #-}
{-# LANGUAGE KindSignatures #-}
{-# LANGUAGE GADTs #-}
data Limit (f :: * -> *) where
  MkLimit :: (forall a. f a) -> Limit f

projectOut :: Limit f -> f a
projectOut (MkLimit fa)  = fa

data Colimit (f:: * -> *) where
  MkCoLimit :: f a -> Colimit f

projectIn :: f a -> Colimit f
projectIn = MkCoLimit

Finite topologies and DFS numbering

In this great math overflow question on How to think about non hausdorff topologies in the finite case, there's an answer that encourages us to think of them as preorders, which are basically graphs. I wanted to understand this perspective, as well as connect it to DFS numbers, since they provide a nice way to embed these topologies into $\mathbb R$.

Closure axioms of topology

We can axiomatize a topology using the kurotawski closure axioms. We need an idempotent monotonic function $c: 2^X \rightarrow 2^X$ which satisfies some technical conditions. Formally:

1. $c(\emptyset) = \emptyset)$ [$c$ is a strict function: it takes bottoms to bottoms]
2. $A \subseteq c(A)$. [monotonicity]
3. $c$ is idempotent: $c(c(A)) = c(A)$. [idempotence]
4. for all $A, B$ in $X$, $c(A \cup B) = c(A) \cup c(B)$.

Under this, a set is closed if it is a fixed point of $c$: That is, a set $A$ is closed iff $c(A) = A$.

Slight weakening into Single axiom version

Interestingly, this also gives a single axiom version of topological axioms, something that maybe useful for machine learning. The single axiom is that for all $A, B \subseteq X$, $A \cup c(A) \cup c(C(B)) \subseteq c(A \cup B)$. This does not provide that $c(\emptyset) = \emptyset$, but it does provide the other axioms [2-4].

Continuous functions

A function is continuous iff $f(c(A)) \subseteq c'(f(A))$ for every $A \in X$.

TODO: give examples of why this works, and why we need $(\subseteq)$ and not just $(eq)$.

Finite topologies as preorders

We draw an arrow $x \rightarrow y$ iff $x \in Closure(y)$. Alternatively stated, draw an arrow iff $Closure(x) \subseteq Closure(y)$. That is, we have an injection from the closure of $x$ into the closure of $y$, and the arrow represents the injection. Alternatively, we can think of this as ordering the elements $x$ by "information". A point $x$ has less information than point $y$ if its closure has fewer points.

T0 in terms of closure:

• $X$ is $T_0$ iff for points $p, q \in X$, we have an open set $O$ which contains one of the points but not the other. Formally, either $p \in O \land q \not \in O$, or $p \not \in O \land q \in O$.
• Example of a $T_0$ space is the sierpinski space. Here, we have the open set ${ \bot }$ by considering the computation f(thunk) = force(thunk). For more on this perspective, see Topology is really about computation . This open set contains only $\bot$ and not $\top$.
• Closure definition: $X$ is $T_0$ iff $x \neq y \implies c({x}) \neq c({y})$

T1 in terms of closure:

• $X$ is $T_1$ iff for all $p, q$ in $X$, we have open sets $U_p, U_q$ such that $U_p, U_q$ are open neighbourhoods of $p, q$ which do not contain the "other point". Formally, we need $p \in U_p$ and $q \not \in U_p$, and similarly $q \in U_q$ and $p \not \in U_q$. That is, $U_p$ and $U_q$ can split $p, q$ apart, but $U_p$ and $U_q$ need not be disjoint.
• Example of $T_1$ is the zariski/co-finite topology on $\mathbb Z$, where the open sets are complements of finite sets. Given two integers $p, q$, use the open sets as the complements of the closed finite sets $U_p = {q}^C = \mathbb Z - q$, and $U_q = {p}^C = \mathbb Z - p$. These separate $p$ and $q$, but have huge intersection: $U_p \cap U_q = Z - { p, q}$.
• Closure definition: $X$ is $T_1$ iff $c({x}) = {x}$.
• T1 has all singleton sets as closed

Haussdorf (T2) in terms of closure

• $X$ ix $T_1$ iff for all $p, q$ in $X$, we have open set $U_p, U_q$ such that they are disjoint ($U_p \cap U_q = \emptyset$) and are neighbourhoods of $p$, $q$: $p \in U_p$ and $q \in U_q$.
• Example of a $T_2$ space is that of the real line, where any two points $p, q$ can be separated with epsilon balls with centers $p, q$ and radii $(p - q) / 3$.
• Closure definition: $X$ is $T_2$ iff $x \neq y$ implies there is a set $A \in 2^X$ such that $x \not \in c(A) \land y \not \in c(X - A)$ where $X - A$ is the set complement.

Relationship between DFS and closure when the topology is $T0$

If the topology is $T0$, then we know that the relation will be a poset, and hence the graph will be a DAG. Thus, whenever we have $x \rightarrow y$, we will get

DFS: the T0 case

DFS: the back edges

Categorical definition of products in painful detail

I feel like I have incorrectly understood, then un-understood, and re-understood in a slightly less broken way the definition of the product in category theory around 5 times. I'm documenting the journey here.

The definition

Given two objects $a, b$, in a category $C$, any 3-tuple $(p \in C, \pi_a \in Hom(p, a), \pi_b \in Hom(p, b))$ is called their product, if for any other 3 tuple $(q \in C, \pi'_a \in Hom(q, a), \pi'_b \in Hom(q, b))$, we have a unique factorization map $f \in Hom(q, p)$ such that $\pi'_a = \pi_a \circ f$, $\pi'_b = \pi_b \circ f$.

(Note that I did not say the product. This is on purpose). We claim that the product is unique up to unique isomorphism.

Let's choose the category to be the category of sets. Let's try and figure out what a product of the sets $a = { \alpha, \beta }$ and $b = { \gamma, \delta }$ is going to be.

Non-example 1: product as ${ 1 }$

Let's try to choose the product set as simply ${ 1 }$, with the maps being chosen as $\pi_a(1) = \alpha; \pi_b(1) = \gamma$:

     πb
p{1}--->{ γ }
  |     { δ }
  |
πa|
  v 
{ α , β }

In this case, it's easy to see the failure. I can build a set $q = { 2 }$ with the maps $\pi'_a(2) = \alpha; \pi'_b(2) = \delta$:

     πb
q{2}-+  { γ }
  |  |  {   }
  |  +->{ δ }
  |
πa|
  v 
{ α , β }

There is a single, unique map which takes $q$ to $p$, which is the function $f: 2 \mapsto 1$. See that $\pi'_b(2) = \delta$, while $\pi_b(f(2)) = \pi_b(1) = \gamma$. Hence the universal property can never be satisfied.

Thus $({ 1 }, 1 \mapsto \alpha, 1 \mapsto \gamma)$ is not a product of ${ \alpha, \beta }$ and ${ \gamma, \delta }$ as it is unable to represent a pair $(\alpha, \delta)$.

Non-example 2: product as ${ 1, 2, 3, 4, 5 }$

In this case, we shall see that we will have too much freedom, so this will violate the "unique map" aspect. Let's pick some choice of $\pi_a$ and $\pi_b$. For example, we can use:

$$ \begin{aligned} (&p = { 1, 2, 3, 4}, \ &\pi_a = 1 \mapsto \alpha, 2 \mapsto \alpha, 3 \mapsto \beta, 4 \mapsto \beta, 5 \mapsto \beta\ &\pi_b = 1 \mapsto \gamma, 2 \mapsto \delta, 3 \mapsto \gamma, 4 \mapsto \delta, 5 \mapsto \delta) \end{aligned} $$

Now let's say we have a set $q = { 42 }$ such that $\pi'_a(42) = \beta, \pi'_b(42) = \delta$.

If we try to construct the map $f: q \rightarrow p$, notice that we get \emph{two} possible legal maps. We can set $f(42) = 4$, or $f(42) = 5$, because both $4$ and $5$ map into $(\beta, \delta)$.

This violates the uniqueness condition of the product. Thus, the set ${1, 2, 3, 4, 5}$ is not a product of ${\alpha, \beta }$ and ${\gamma, \delta }$ because it does not provide a unique map from $q$ into $p$. Alternatively, it does not provide a unique representation for the tuple $(\beta, \delta)$. Thus it can't be a product.

Checking an example: ${ \alpha, \beta } \times { \gamma , \delta }$ as ${1, 2, 3, 4}$

I claim that a possible product of $a$ and $b$ is:

$$ \begin{aligned} (&p = { 1, 2, 3, 4}, \ &\pi_a = 1 \mapsto \alpha, 2 \mapsto \alpha, 3 \mapsto \beta, 4 \mapsto \beta,\ &\pi_b = 1 \mapsto \gamma, 2 \mapsto \delta, 3 \mapsto \gamma, 4 \mapsto \delta) \end{aligned} $$

p       πa            a
   1------------*--->{α}
   |  2--------─┘    { }
   |  | 3-------*--->{β}
   |  | | 4----─┘
   +----* |
πb |  |   |
   |  *---+
   |      |
   v      v
b {γ      δ}

Now given a 3-tuple $(q, \pi'_a \in Hom(q, a), \pi'_b \in Hom(q, b))$, we construct the factorization map $f: q \rightarrow p$, where: $$ f: q \rightarrow p; \quad f(x) \equiv \begin{cases} 1 & \pi'_a(x) = \alpha \land \pi'_b(x) = \gamma \ 2 & \pi'_a(x) = \alpha \land \pi'_b(x) = \delta \ 3 & \pi'_a(x) = \beta \land \pi'_b(x) = \gamma \ 4 & \pi'_a(x) = \beta \land \pi'_b(x) = \delta \ \end{cases} $$

That is, we build $f(x)$ such that on composing with $\pi_a$ and $\pi_b$, we will get the right answer. For example, if $\pi'_a(x) = \alpha$, then we know that we should map $x$ to an element $y \in p$ such that $\pi(y) = \alpha$. So we need $y = 1 \lor y = 2$. Then looking at $\pi'_b(x)$ allows us to pick a unique y. There is zero choice in the construction of $f$. We need exactly 4 elements to cover all possible ways in which $q$ could map into $a$ and $b$ through $\pi'_a, \pi'_b$ such that we cover all possibilities with no redundancy.

This choice of product is goldilocks: it does not have too few elements such that some elements are not representable; it also does not have too many elements such that some elements are redundant.

Non uniqueness: product as ${10, 20, 30, 40}$

Note that instead of using $p = {1, 2, 3 4}$, I could have used $p = {10, 20, 30, 40 }$ and nothing would have changed. I have never depended on using the values $1, 2, 3, 4$. Rather, I've only used them as \emph{labels}.

Non uniqueness: product as ${ (\alpha, \gamma), (\alpha, \delta), (\beta, \gamma), (\beta, \delta) }$

Indeed, our usual idea of product also satisfies the product, since it is in unique isomorphism to the set ${1, 2, 3, 4}$ we had considered previously. But this might be strange: Why is it that the categorical definition of product allows for so many other "spurious" products? Clearly this product of tuples is the best one, is it not?

Of course not! Inside the category of sets, anything with the same cardinality is isomorphic. So nothing inside the category can distinguish between the sets ${1, 2, 3, 4}$ and ${ (\alpha, \gamma), (\alpha, \delta), (\beta, \gamma), (\beta, \delta) }$. Hence, the usual product we are so used to dealing with is not privileged.

This should make us happy, not sad. We have removed the (un-necessary) privilege we were handing to this one set because it "felt" like it was canonical, and have instead identified what actually makes the product of sets tick: the fact that their cardinality is the product of the cardinalities of the individual sets!

How to think about the product

Since we are specifying the data of $(p, \pi_a, \pi_b)$, we can simply think of elements of $p$ as being "pre-evaluated", as $(x \in p, \pi_a(x), \pi_b(x))$. So in our case, we can simplify the previous situation with $(p = { 10, 20, 30, 40 }, \pi_a, \pi_b)$ by writing the set as $p = { (10, \alpha, \gamma), (20, \alpha, \delta), (30, \beta, \gamma), (40, \beta, \delta) }$. This tells us "at a glance" that every element of $a \times b$ is represented, as well as what element it is represented by.

Proof of uniqueness upto unique isomorphism

• Assume we have two products $(p, \pi_a, \pi_b)$ and $(q, \pi_a, \pi_b)$, which are products of $a$ and $b$
• By the universality of $p$ wrt $q$, we get a unique! map $q2p$ such that the diagaram commutes.
• By the universality of $q$ wrt $p$, we get a unique! map $p2q$
• We get a map $q2p \cdot p2q : p \rightarrow p$. by the universality of $p$ with respect to $p$, we get a unique! map that makes the diagram commute.But we have two such maps: $id_p$ as well as $q2p . p2q$. Hence we must have $id_p = q2p \cdot p2q$. In pictures:

          ∃!id(p)
          +---+
          |   |
          |   v
+---------ppppp--------+
| πa      |   ^     πb |  
v      ∃!p2q  |        v
a         |   |        b
^         |  ∃!q2p     ^
| π'b     v   |    π'b |
+---------qqqqq--------+

• The full diagram commutes.
• By definition of identity/commutativity of the diagram, $\pi_a \circ id_p = \pi_a$.
• By definition of identity/commutativity of the diagram, $\pi_b \circ id_p = \pi_b$.
• By the commutativity of the diagram, we have $\pi_a \circ (q2p \circ p2q) = \pi_a$.
• By the commutativity of the diagram, we have $\pi_b \circ (q2p \circ p2q) = \pi_b$.
• We can consider the universal property of the product, where we have $(p, \pi_a, \pi_b)$ as one product, and $(p, \pi_a , \pi_b)$ as another product.
• This gives us a unique map $h$ such that $\pi_a \circ h = \pi_a$, and $\pi_b \circ h = \pi_b$.
• We have two candidates for $h$: $h = id_p$ and $h = p2q \circ q2p$. Hence, by the uniqueness of $h$, we have that $id_p = p2q \circ q2p$.

Wrapping up

• Link to a misconception of the proof I had carried around for ages

Why is the spectrum of a ring called so?

I've been watching Ravi Vakil's excellent "pseudolectures" on algebraic geometry, aptly titled AGITTC: Algebraic geometry in the time of Covid. In lecture 3, there was a discussion going on in the sidebar chat where a user said that the name "prime sprectrum" came from something to do with quantum mechanics. To quote:

letheology: spectrum of light -> eigenvalues of the hamiltonian operator -> prime ideal of the polynomial ring of the operator

I don't know what the prime ideal of the polynomial ring of the operator is, so let's find out! I got a somewhat incomplete answer on math.se

Another user said:

Lukas H: I like the definition of Spec A that doesn't include the word prime ideal, by a colimit of Hom(A, k) where k run over all fields and the maps are morphisms that make the diagrams commute.

That's a pretty crazy definition. One can apparently find this definition in Peter Schloze's notes on AG. I got an answer for this on math.se

Ergo proxy

I've been watching the anime "Ergo Proxy". I'll keep this section updated with things I find intriguing in the anime.

• bios stood for both bow and life in greek, supposedly. Both lead to death. This is an interesting fact. I wonder if the BIOS of our computers is also from this, and was they backronymed into basic input/output system.

• "the white noise that reverberates within the white darkness is life itself". I have no idea what this means. It's a great sentence for sure.

Satisfied and frustrated equations

I found this interesting terminology on a wiki walk

• An edge is satisfied if some equation y = f(x) is satisfied.
• Otherwise, the edge is said to be frustrated.

This is far more evocative terminology than UNSAT/unsatisfied, and also makes for good haskell like variable names. ss for satisfied equations, fs for frustrated equations!

Combinatorial intuition for Fermat's little theorem

We wish to show that $x^p \equiv x (\mod p)$ combinatorially. Let's take $2^3 (\mod 3)$ for simplicity. The general case follows. Let's first write down strings which enumerate $2^3$:

000
001
010
011
100
101
110
111

To make use of $\mod 3$, we're going to treat our strings as necklaces. So, for example, the string 011 looks like:

*-→ 0 -*
|      |
|      ↓
1 ←--- 1

So we have three possible rotations of the string 011:

011
110
101

• Each of these rotations are unique, since they can be totally ordered using lexicographic ordering. Indeed, for any string other than 000, 111, all of its rotations are unique.

• So we can count the above 7 strings with equivalence class representatives. These representatives are those strings that are the lex smallest in their cyclic shifts. (Why are cyclic shifts so important?)

Cyclic subshifts of strings:
---------------------------
000, 000, 000
001, 010, 100
011, 110, 101
111, 111, 111

• We've written the strings along with their cyclic subshifts, with the representative of the equivalence class as the first element. So the representatitives are 000, 001, 011, 111. Note that two of these (000, 111) are equal to their cyclic subshifts. All of the others are distinct, and generate 3 elements.

• So we can count the above strings as:

all strings   = {shifts of 001, 011}U{000, 111}
|all strings| = |{shifts of 001, 011}|+|{000, 111}|
no. of shifts = 3*(no. of representatives)
2^3 = 3 * (no. of representatives) + 2
2^3 = 3 * (no. of representatives) + 2
2^3 % 3 = 2

In general, for x^p % p, we will get x strings that contain the same letter. These will not have elements in their cyclic shift equivalence classes. The other strings will be generated as the smallest cyclic subshift of some string.

Why does this not work when p is not prime?

Let p = 4. In this case, I can pick the string s = 0101. It has shifts:

0101 <-
1010
0101 <-
1010

so two of its shifts overlap, hence we will double-count the string 0101 if I counted its equivalence class as having size 4.

Relationship to group theory?

• How does this relate to group theory? Well, what we are doing is providing an action of the group Z/pZ into the set of strings X^p where X is some set. Our group action for a number n ∈ Z/pZ takes a string s ∈ X^p to its cyclic shift by n characters.

• We are then using the fact that the orbits of an action when p is prime has size either 1 or p, since the size of the orbit divides the size of the group Z/pZ, which is p, a prime. The divisors of p are only 1 and p. Therefore, the size of the orbit is either 1 or p.

• Only necklaces that have identical elements like 000 and 111 have orbits of size 1. We have |X| such necklaces.

• All other necklaces have size p.

• The rest of the proof follows similarly as before.

References

• A string of pearls: proofs of Fermat's little theorem
• Algorithms thread 1: division under mod

An incorrect derivation of special relativity in 1D

I record an incorrect derivation of special relativity, starting from the single axiom "speed of light is constant in all inertial reference frames". I don't understand why this derivation is incorrect. Help figuring this out would be very appreciated.

The assumption

We assume that the velocity of light as measured by any inertial frame is constant. Thus if $x, x'$ are the locations of light as measured by two inertial frames, and $t, t'$ is the time elapsed as measured by two inertial frames, we must have that $dx/dt = dx'/dt'$. This ensures that the speed of light is invariant.

The derivation

• Our coordinate system has an $x$ space axis and a $t$ time axis.
• We have observer (1) standing still at the origin, and measures time with a variable $t$.
• We have observer (2) moving to the left with a constant velocity $v$.
• Observer (1) who is at rest sees a photon starting from the origin travelling towards the right with constant velocity $c$. The position of the photon at time $t$ is $x = c t$.
• Observer (2) also sees this photon. At time $t$, he sees the position of the photon as $x' = vt + ct$.
• From our rule of invariance, we have that $dx/dt = c = dx'/dt'$.

We calculate $dx'/dt' = (dx'/dt)(dt/dt')$ [chain rule], giving:

$$ \begin{aligned} &c = \frac{dx}{dt} = \frac{dx'}{dt'} = \frac{dx'}{dt} \frac{dt}{dt'} \ &c = \frac{d(vt + ct)}{dt}\frac{dt}{dt'} \ &c = (v + c) \frac{dt}{dt'} \ &\frac{c}{v+c} = \frac{dt}{dt'} \ &dt' = (v+c)dt/c \ &t' = (v+c)t/c = (1 + v/c) t \end{aligned} $$

So we get the relation that time elapsed for observer (2) is related to observer (1) as $t' = (1 + v/c) t$.

• This checks out: Assume our observer is moving leftward at $v = c$. He will then see the photon move rightward at $x' = 2ct$. So if his time slows down to have $t' = 2t$, we will have that $x/t' = 2ct/2t = c$.

• However, this forumla allows us to go faster than the speed of light with no repercurssions! (It is also not the correct formula as anticipated by the usual derivation). This can be fixed.

• Now assume that Observer 2 was moving rightward, not leftward. That is, we simply need to set $v = -v$, since this change of sign accomplishes flipping the direction of motion in 1D. This gives us the equation $t' = (1 - v/c)t$.

• According to this new equation, we are not allowed to approach the speed of light. If we attempt to do so, we will need to elapse zero time; and if we exceed the speed of light, we will need to elapse negative time.

• However, these formulae lead to an absurdity. If our observer 1 and observer 2 witness two photons, one moving leftward and one moving rightward, one will need to write down the equations $t' = (1 \pm v/c)t$, which plainly leads one to contradiction.

What's the issue?

The issue is the equation $x' = vt + ct$.

• It is true that as per observer (1) standing at the origin, the distance between observer (2) and the photon is $vt + ct$.
• It is not true that observer(2) sees the distance between them and the photon as $vt + ct$.
• Intuitively, this equation of $x' = vt + ct$ completely ignores length contraction, and hence cannot be right.
• Alternatively, the equation of $x' = vt + ct$ imposes galilean relativity, where I am attempting to naively connect reference frames, which cannot be correct.

The geometry and dynamics of magnetic monopoles

I found this cool document written by Sir Atiyah, called as "The geometry and dynamics of magnetic monopoles" which contains a nice exposition of electromagnetism from the differential viewpoint. I'll record what I read here.

Sanskrit and Sumerian

Sanskrit's precursors

The oldest known sanskrit text that has been found is the Rig Veda. Eveyrthing after is the study of sanskit proper. This is quite problematic because the Rig Veda is a complete and consistent textbook with respect to language. It's a black-box in terms of language evolution.

The question "what is the precursor" asks for a method of study to determine the precursor. We just don't know because we have no writings, text, etc.

Archaeological data

Archaeological data is problematic as well. We don't know where the people who knew sanskrit came from. Sanskrit was spoken in the northen part of Hindusthan [what they originally called Bhrahma-nagar (?)]. While we can try to undersatnd where it comes from, it's hard. The script is Brahmi / Devanagiri, which means used by Brahma or god. The name "sanskrit" is a compound that stands for "well-formed". It's really clean-slate in that sense. The study of Indo-Aryan languages in the Indian subcontinent has only one possible known history, which stops at the Rig Veda. We don't know the relationship between 2400BC when Rig Veda was written to anything before it.

Non Vedic sanskrit

Studies in non-vedic sanskrit is known to be the "true" proto-Indo-Europoean (PIE) language. The conjecture is that this Indo European language ought to be able to cover middle greek, hittite, and sanskit.

Prakrit and its relationship to this story

Prakrit evolved as a vernacular of Sanskrit in the north pahadi region. Hindi as we know toady evolved from Hindusthani, which came from languages in northern india. Languages like Marathi, Marvadi, Gujurathi, etc. came a lot before Hindi did.

TLDR on Sanskrit v/s Hindi

There is a huge gap of time between Sanskit, Prakrit, Pali, and Hindi. Hindi evolved around the 1600s due to the Mughals who used to speak a vernacular of Hindusthani. Kabir also wrote in Hindusthani. There was also some Farsi and Urdu mixed in.

Hindi is more of a political exploit than an actual language ~ Alok 2020

The relationship to Sumerian

We don't know what the relationship to sumerian is. Social expectations that was setup is sumerian has become more stringent in Sanskrit.

Writing Cuneiform

I've been reading about the Sumerian people, and I've gotten fascinated with the question of how to write in Cuneiform, which is their script. I wanted to learn how to write cuneiform. It appears that it was originally written down by pressing reed styluses into clay. The script is syllabic in nature. We have three components:

1. Vertical wedge 𐏑
2. Horizontal wedge 𐎣
3. Diagonal 𐏓

References

• Getty museum: Writing cuneiform
• Irving Finkel teaches how to write cuneiform
• CLDI: Cuneiform Digital library initiative
• Font: Old persian block

The code of hammurabi

I've wanted to read the code of hammurabi since it was name dropped in Snow Crash by Neal Stephenson. I finally got around to it. Here's some excerpts I found fascinating. The numbers are according to this translation of the Code of Hammurabi. Some helpful hints were found from the Avalon ancient law codes page of the Yale law school.

• (5) If a judge try a case, reach a decision, and present his judgment in writing; if later error shall appear in his decision,and it be through his own fault, then he shall pay twelve times the fine set by him in the case, and he shall be publicly removed from the judge’s bench, and never again shall he sit there to render judgement. (Commentary: These are steep penalties for getting a case wrong. I suppose this encouraged innocent until proven guilty quite a bit.)

• (23) If the robber is not caught, then shall he who was robbed claim under oath the amount of his loss; then shall the community, and...on whose ground and territory and in whose domain it was compensate him for the goods stolen (Commentary: This rule appears to setup some sort of insurance where someone who is robbed is guaranteed recompence)

• (108) If a tavern-keeper (feminine) does not accept corn according to gross weight in payment of drink, but takes money, and the price of the drink is less than that of the corn, she shall be convicted and thrown into the water. (Commentary: I wonder why this rule specifically singles out women)

• (120) If any one store corn for safe keeping in another person’s house, and any harm happen to the corn in storage, or if the owner of the house open the granary and take some of the corn, or if especially he deny that the corn was stored in his house: then the owner of the corn shall claim his corn before God (on oath), and the owner of the house shall pay its owner for all of the corn that he took. (Commentary: I wonder whether there were many 'owners of corn' who swore false oaths. I suppose not, if this rule was enshrined into law. It is interesting that they held oaths to god as a mechanism to prevent lying)

• (137) 137. If a man wish to separate from a woman who has borne him children, or from his wife who has borne him children: then he shall give that wife her dowry, and a part of the usufruct offield, garden, and property, so that she can rear her children.When she has brought up her children, a portion of all that is given to the children, equal as that of one son, shall be given to her. She may then marry the man of her heart. (Commentary: their society seems egalitarian, and provides both a mechanism of divorce, and rights and property to the wife after divorce).

• (168) If a man wish to put his son out of his house, and declare before the judge: “I want to put my son out,” then the judge shall examine into his reasons. If the son be guilty of no great fault, for which he can be rightfully put out, the father shall not put him out; (169). If he be guilty of a grave fault, which should rightfully deprive him of the filial relationship, the father shall forgive him the first time; but if he be guilty of a grave fault a second time the father may deprive his son of all filial relation. (Commentary: I find this notion of 'forgive once' being encoded into law very interesting. I don't know of other law codes that have such a thing).

• (188). If an artizan has undertaken to rear a child and teaches him his craft, he can not be demanded back; (189) If he has not taught him his craft, this adopted son may return to his father’s house. (Commentary: I find it interesting that this notion of 'taking a son' is intertwined with caring for the son and teaching them a craft to become a future productive member of society)

• (196) If a man put out the eye of another man, his eye shall be put out. [ An eye for an eye ]. (Commentary: Fascinating that 'eye for an eye' comes from the code).

• (202). If any one strike the body of a man higher in rank than he,he shall receive sixty blows with an ox-whip in public. (Commentary: Neat how one can glean the existence of a social hierarchy from a law code. I wonder how this hierarchy was defined.)

• (215) If a physician make a large incision with an operating knife and cure it, or if he open a tumor (over the eye) with an operating knife, and saves the eye, he shall receive ten shekels in money. (Commentary: (i) It is weird that things like doctor's procedures are covered in the law code. How often is the code revised? What happens when a doctor comes up with a new treatment? (ii) It is weird that the prices are recorded in the law code. What about inflation?)

• (249) If any one hire an ox, and God strike it that it die, the man who hired it shall swear by God and be considered guiltless. (Commentary: Once again, their belief in the truthfulness of oaths sworn to God. Also, it's nice to know that they do understand and account for truly random events that one has no control over)

• Epilogue: In future time, through all coming generations, let the king,who may be in the land, observe the words of righteousness which I have written on my monument; let him not alter the law of the land which I have given, the edicts which I have enacted; my monument let him not mar. If such a ruler have wisdom, and beable to keep his land in order, he shall observe the words which I have written in this inscription (Commentary: This advice for future kings is interesting, and appears to imply that the rules and all the prices in the rules ought to be immutable. I really do wonder how they dealt with their society changing, new inventions, and inflation)

• Taken from this introduction to the code of hammurabi from Yale: An accused person was allowed to cast himself into "the river," the Euphrates. Apparently the art of swimming was unknown; for if the current bore him to the shore alive he was declared innocent, if he drowned he was guilty. So we learn that faith in the justice of the ruling gods was already firmly, though somewhat childishly, established in the minds of men

The implicit and inverse function theorem

I keep forgetting the precise conditions of these two theorems. So here I'm writing it down as a reference for myself.

Implicit function: Relation to function

• Example 1: $x^2 + y^2 = 1$ to $y = \sqrt{1 - x^2}$.

If we have a function $y = g(p, q)$, we can write this as $y - g(p, q) = 0$. This can be taken as an implicit function $h(y; p, q) = y - g(p, q)$. We then want to recover the explicit version of $y = g'(p, q)$ such that $h(g'(p, q); p, q) = 0$. That is, we recover the original explicit formulation of $y = g'(p, q)$ in a way that satisfies $h$.

The 1D linear equation case

In the simplest possible case, assume the relationship between $y$ and $p$ is a linear one, given implicitly. So we have $h(y; p) = \alpha y + \beta p + \gamma = 0$. Solving for $h(y,p) = 0$, one arrives at: $y = -1/\alpha (\beta p + \gamma)$.

• Note that the solution exists iff $\alpha \neq 0$.
• Also note that the the existence of the solution is equivalent to asking that $\partial h / \partial y = \alpha \neq 0$.

The circle case

In the circle case, we have $h(y; p) = p^2 + y^2 - 1$. We can write $y = \pm \sqrt{p^2 - 1}$. These are two solutions, not one, and hence a relation, not a function.

• We can however build two functions by taking two parts. $y+ = +\sqrt{p^2 - 1}$; $y- = -\sqrt{p^2 - 1}$.

• In this case, we have $\partial h / \partial y = 2y$, which changes sign for the two solutions. If $y^\star > 0$, then $(\partial h / \partial y)(y^\star = 0)$. Similarly for the negative case.

Assuming that a solution for $h(y, p)$ exists

Let us say we wish to solve $h(y; p) = y^3 + p^2 - 3 yp - 7 = 0$. Let's assume that we have a solution $y = sol(p)$ around the point $(y=3, p=4)$. Then we must have: $sol(p)^3 + p^2 - 3 sol(p) p - 7 = 0$. Differentiating by $p$, we get: $3 sol(p)^2 sol'(p) + 2p - 3 sol'(p) p - 3 sol(p) = 0$. This gives us the condition on the derivative:

$$ \begin{aligned} &3 sol(p)^2 sol'(p) + 2p - 3 sol'(p) p - 3 sol(p) = 0 \ &sol'(p)\left[ 3 sol(p)^2 - 3p \right] = 3 sol(p) - 2p \ &sol'(p) = [3 sol(p) - 2p] / \left[ 3(sol(p)^2 - 3p) \right] \ \end{aligned} $$

The above solution exists if $3(sol(p)^2 - 3p \neq 0)$. This quantity is again $\partial h / \partial y$.

Application to economics

• We have two inputs which are purchaed as $x_1$ units of input 1, $x_2$ units of input $2$.
• The price of the first input is $w_1 BTC/unit$. That of the second input is $w_2 BTC/unit$.
• We produce an output which is sold at price $w BTC/unit$.
• For a given $(x_1, x_2)$ units of input, we can produce $x_1^a x_2^b$ units of output where $a + b < 1$. The Coob-douglas function.
• The profit is going to be $profit(x_1 x_2, w_1, w_2, w) = w(x_1^a x_2^b) - w_1 x_1 - w_2 x_2$.
• We want to select $x_1, x_2$ to maximize profits.
• Assume we are at break-even: $profit(x_1, x_2, w_1, w_2, w) = 0$.
• The implicit function theorem allows us to understand how any variable changes with respect to any other variable. It tells us that locally, for example, that the number of units of the first input we buy ($x_1$) is a function of the price $w_1$. Moreover, we can show that it's a decreasing function of the price.

Inverse function: Function to Bijection

• Given a differentiable function $f$, at a point $p$, we will have a continuous inverse $f^{-1}(p)$ if the derivative $f'(p)$ is locally invertible.

• The intuition is that we can approximate the original function with a linear function. $y = f(p + \delta) = f(p) + f'(p) \delta$. Now since $f'(p)$ is locally invertible, we can solve for $\delta$. $y = f(p) + f'(p) \delta$ implies that $\delta = 1/f'(p) [y - f(p + \delta) ]$. This gives us the pre-image $(p + delta) \mapsto y$.

• The fact that $1/f'(p)$ is non-zero is the key property. This generalizes in multiple dimensions to saying that $f'(p)$ is invertible.

One perspective we can adopt is that of Newton's method. Recall that Newton's method allows us to find $x^$ for a fixed $y^$ such that $y^* = f(x^*)$. It follows the exact same process!

• We start with some $x[1]$.
• We then find the tangent $f'(x[1])$.
• We draw the tangent at the point $x[1]$ as $(y[2] - y[1]) = f'(x[1])(x[2] - x[1])$.
• To find the $y^$ we set $y[2] = y^$.
• This gives us $x[2] = x[1] - (y^* - y[1])/f'(x[1])$.
• Immediately generalizing, we get $x[n+1] = x[n] - (y^* - y[n]) / f'(x[n])$.

Idea of proof of implicit function theorem (from first principles)

• Let $F(x, y) \neq 0$, point $p$ be the point where we wish to implicitize.
• To apply implicit fn theorem, take $\partial_y|_pF(x, y) \neq 0$. Say WLOG that $\partial_y|_p F(x, y) > 0$, since $F$ is assumed to be continuously differentiable.
• Since $\partial_y F$ is continuous and positive at $p$, it's positive in a nbhd of $p$ by continuity.
• Consider $F(p_x, y)$ as a single variable function of $y$. Its derivative with respect to $y$ is positive; it's an increasing function in terms of $y$.
• Since $F(x_0, y_0)$ and is an increasing function of $y_0$, we must have two $y$ values $y_-, y_+$ such that $F(p_x, y_+)$ is positive, and $F(p_x, y_-)$ is negative.
• Since $F$ is zero and continuous, we have that for all $x$ near $x_0$, that $F(x_0, y_+) > 0 \implies F(x, y_+) > 0$ and $F(x_0, y_-) < 0 \implies F(x, y_-) < 0$. We have released $x_0$ into a wild $x$ in the neighbourhood!
• Now pick some $x_$ near $x$. Since we have that $F(x_, y_+) > 0$ and $F(x_, y_-) < 0$, there exists a unique $y_$ (by MEAN VALUE THEOREM) that $F(x_, y_) = 0$
• Since the $y_$ is unique, we found a function: $x_ \xmapsto{f} y_*$.
• We are not done. We need to prove the formula for $f'(x)$ where $f$ is the implicit mapping.
• $F(x, f(x)) = 0$ by defn of $f(x)$. Apply chain rule!

\begin{aligned} &F(x, f(x)) = 0 \ &dF = 0 \ &\frac{\partial F}{\partial x} \cdot \frac{\partial x}{\partial x} + \frac{\partial F}{\partial y} \frac{df}{dx} = 0 \ &\frac{\partial F}{\partial x} \cdot 1 + \frac{\partial F}{\partia