johnhw / Differentiable_sorting
Labels
Projects that are alternatives of or similar to Differentiable sorting
Differentiable parallel approximate sorting networks
A Python implementation of a fully-differentiable approximate sorting function for power-of-2 length vectors. Uses Numpy, PyTorch or Tensorflow (or autograd, JAX or cupy), but trivial to use in other backends. Works on GPU.
from differentiable_sorting import bitonic_matrices, diff_sort, diff_argsort
# sort 8 element vectors
sort_matrices = bitonic_matrices(8)
x = [5.0, -1.0, 9.5, 13.2, 16.2, 20.5, 42.0, 18.0]
print(diff_sort(sort_matrices, x))
>>> [-1.007 4.996 9.439 13.212 15.948 18.21 20.602 42. ]
# we can relax towards averaging by plugging in another
# softmax function to the network
from differentiable_sorting import softmax_smooth
print(diff_sort(sort_matrices, x, lambda a,b: softmax_smooth(a,b, 0.0))) # as above
>>> [-1.007 4.996 9.439 13.212 15.948 18.21 20.602 42. ]
print(diff_sort(sort_matrices, x, lambda a,b: softmax_smooth(a,b, 0.05))) # smoothed
>>> [ 1.242 5.333 9.607 12.446 16.845 18.995 20.932 37.999]
print(diff_sort(sort_matrices, x, lambda a,b: softmax_smooth(a,b, 1.0))) # relax completely to mean
>>> [15.425 15.425 15.425 15.425 15.425 15.425 15.425 15.425]
print(np.mean(x))
>>> 15.425
###### Ranking
# We can rank as well
x = [1, 2, 3, 4, 8, 7, 6, 4]
print(diff_argsort(sort_matrices, x))
>>> [0. 1. 2. 3. 7. 6. 5. 3.]
# smoothed ranking function
print(diff_argsort(sort_matrices, x, sigma=0.25))
>>> [0.13 1.09 2. 3.11 6.99 6. 5. 3.11]
# using autograd to differentiate smooth argsort
from autograd import jacobian
jac_rank = jacobian(diff_argsort, argnum=1)
print(jac_rank(sort_matrices, np.array(x), 0.25))
>>> [[ 2.162 -1.059 -0.523 -0.287 -0.01 -0.018 -0.056 -0.21 ]
[-0.066 0.562 -0.186 -0.155 -0.005 -0.011 -0.035 -0.105]
[-0.012 -0.013 0.041 -0.005 -0. -0.001 -0.002 -0.008]
[-0.012 -0.025 -0.108 0.564 -0.05 -0.086 -0.141 -0.14 ]
[-0.001 -0.001 -0.003 -0.005 0.104 -0.058 -0.028 -0.008]
[-0. -0.001 -0.002 -0.004 -0.001 0.028 -0.012 -0.007]
[-0. -0. -0.001 -0.002 -0.016 -0.018 0.038 -0.001]
[-0.012 -0.025 -0.108 -0.209 -0.05 -0.086 -0.141 0.633]]
Caveats:
-
May not be very efficient (!), requiring approximately
log_2(n)^2matrix multiplies of sizen x n. These are just permutations, so can also be efficiently implemented via indexing, requiring2nindexing operations per layer. -
Dynamic range is limited, especially with
float32. Very large or very small values will cause trouble. Values distributed between 1 and ~300 work reasonably withfloat64(and similarly for negative values). Values of magnitude 0.0-1.0 are troublesome. Inputs should be pre-normalised (e.g. batch-norm followed by a constant scale by 100) -
The networks are theoretically differentiable, but gradients may be very small for larger networks.
-
This appears to be a variation of the idea presented in NeuroSort by Grover et al. Grover, A., Wang, E., Zweig, A., & Ermon, S. (2019). Stochastic optimization of sorting networks via continuous relaxations. arXiv preprint arXiv:190 3.08850.
Vector sorting
We can also sort vector valued entries using a particular "key" function, assuming this function is also differentiable (e.g. sort a matrix by a particular column) using vector_sort:
vector_sort(
bitonic_matrices(4),
np.array([[1, 5],
[30, 30],
[6, 9],
[80, -2]]),
lambda x: (x @ [1,0]), # sort by column 1
alpha=1.0
)
>>> array( [[80. , -2. ],
[30. , 30. ],
[ 5.97, 8.97],
[ 1.03, 5.03]])
vector_sort(
bitonic_matrices(4),
np.array([[1, 5],
[30, 30],
[6, 9],
[80, -2]]),
lambda x: (x @ [0,1]), # sort by column 2
)
>>> array([[30. , 30. ],
[ 5.91, 8.93],
[ 1.16, 5.07],
[79.93, -1.99]])
Custom comparator functions
It is also possible to sort using any differentiable comparator function:
np.random.seed(31)
x = np.random.normal(0,100,8)
print(x)
>>> [-41.48 -33.34 8.11 -79.1 -21.86 -76.32 -77.71 184.94]
def compare_fn(a,b):
# "clamped abs"
return np.tanh(a**2 - b**2)
matrices = bitonic_matrices(8)
sorted_x = comparison_sort(matrices, x, compare_fn)
print(sorted_x)
>>> [184.94 -79.1 -77.71 -76.32 -41.48 -33.34 -21.86 8.11]
This makes it possible to sort data like images or signals, as well as plain old numbers.
Bitonic sorting
Bitonic sorts create sorting networks with a sequence of fixed conditional swapping operations executed on an n element vector in parallel where, n=2^k.
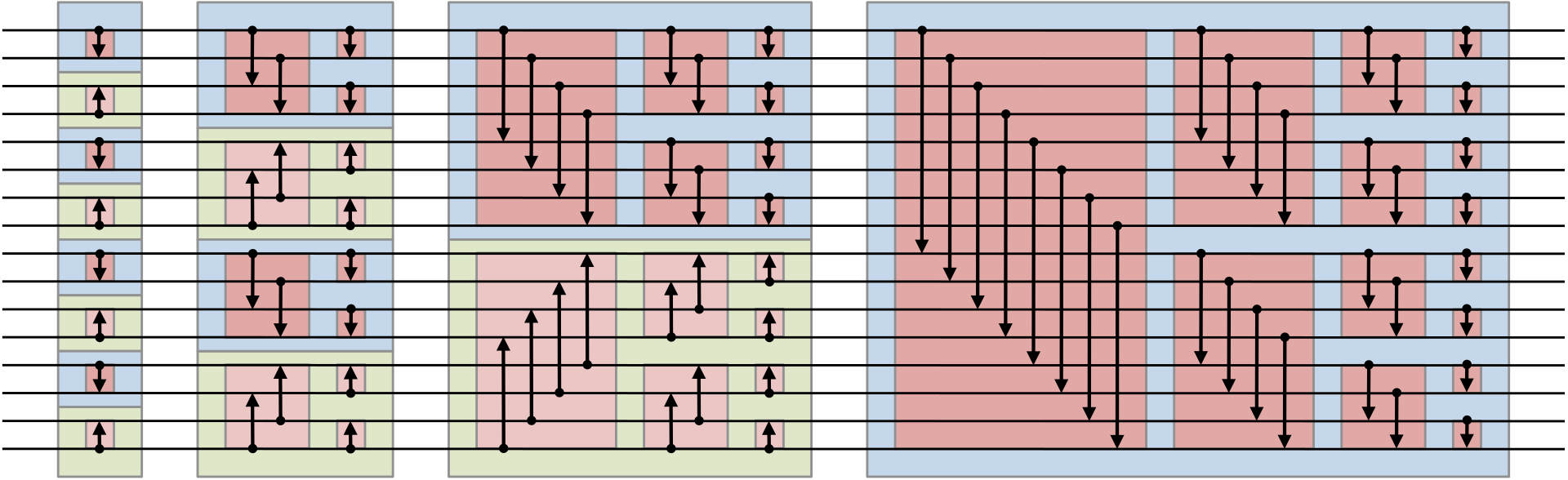
Image: from Wikipedia, by user Bitonic, CC0
The sorting network for n=2^k elements has k(k-1)/2 "layers" where parallel compare-and-swap operations are used to rearrange a n element vector into sorted order. The sequence of operations is independent of the data.
Differentiable compare-and-swap
If we define the softmax(a,b) function (not the traditional "softmax" used for classification, but rather log-sum-exp!) as the continuous approximation to the max(a,b) function,
softmax(a,b) = log(exp(a) + exp(b)).
then
softmin(a,b) = a + b - softmax(a,b).
[Alternatively softmin(a,b) = -log(exp(-a) + exp(-b)) but this adds numerical instability]
Notice that we now have a differentiable compare-and-swap operation:
softcswap(a,b) = (softmin(a,b), softmax(a,b))
We can alternatively use:
smoothmax(a,b, alpha) = (a * exp(a * alpha) + b * exp(b * alpha)) /
(exp(a * alpha) + exp(b * alpha))
which has a configurable alpha term, allowing interpolation between a hard maximum (alpha -> infinity) and mean averaging (alpha -> 0).
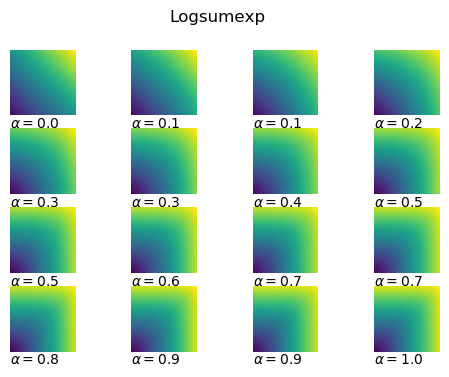
Softmax/logsumexp/quasimax across the range [-5, 5] for various alpha.
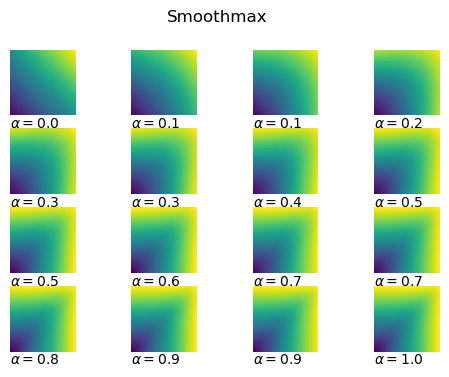
Smoothmax across the range [-5, 5] for various alpha.
Differentiable sorting
For each layer in the sorting network, we can split all of the pairwise comparison-and-swaps into left-hand and right-hand sides. We can any write function that selects the relevant elements of the vector as a multiply with a binary matrix.
For each layer, we can derive two binary matrices left and right which select the elements to be compared for the left and right hands respectively. This will result in the comparison between two n/2 length vectors. We can also derive two matrices l_inv and r_inv which put the results of the compare-and-swap operation back into the right positions in the original vector.
The entire sorting network can then be written in terms of matrix multiplies and the softcswap(a, b) operation.
def softmax(a, b):
return np.log(np.exp(a) + np.exp(b))
def softmin(a, b):
return a + b - softmax(a, b)
def softcswap(a, b):
return softmin(a, b), softmax(a, b)
def diff_bisort(matrices, x):
for l, r, l_inv, r_inv in matrices:
a, b = softcswap(l @ x, r @ x)
x = l_inv @ a + r_inv @ b
return x
The rest of the code is simply computing the l, r, l_inv, r_inv matrices, which are fixed for a given n.
If we're willing to include a split and join operation, we can reduce this to a single n x n multiply for each layer (plus one extra multiply at the start) by fusing consecutive permutations:
def diff_sort_weave(fused, x, softmax=np.maximum):
""" Given a set of bitonic sort matrices generated by
bitonic_woven_matrices(n), sort a sequence x of length n. """
split = len(x) // 2
x = fused[0] @ x # initial permutation
for mat in fused[1:]:
a, b = x[:split], x[split:]
mx, mn = softcswap(a, b)
x = mat @ np.concatenate([mn, mx])
return x
Libraries
The base code works with NumPy. If you want to use autograd jax or cupy then install the autoray package.
pip install autoray
The code should then automatically work with whatever backend you are using if you pass arrays from the right backend.
PyTorch and Tensorflow
PyTorch is supported:
import torch
from differentiable_sorting.torch import bitonic_matrices, diff_sort
from torch.autograd import Variable
x = [5.0, -1.0, 9.5, 13.2, 16.2, 20.5, 42.0, 18.0]
matrices = bitonic_matrices(8)
torch_input = Variable(torch.from_numpy(np.array(x)).float(), requires_grad=True)
result = diff_sort(matrices, torch_input)
print(result)
>>> tensor([-1.0075, 4.9958, 9.4394, 13.2117, 15.9480, 18.2103, 20.6023, 42.0000],
grad_fn=<AddBackward0>)
print(torch.autograd.grad(result[0], torch_input)[0])
>>> tensor([7.3447e-03, 9.9257e-01, 8.1266e-05, 3.9275e-06, 3.4427e-08, 1.4447e-09,
0.0000e+00, 9.5952e-09])
Tensorflow is also supported:
import tensorflow as tf
from differentiable_sorting.tensorflow import bitonic_matrices, diff_sort, diff_argsort
tf_input = tf.reshape(tf.convert_to_tensor([5.0, -1.0, 9.5, 13.2, 16.2, 20.5, 42.0, 18.0], dtype=tf.float64), (-1,1))
tf_output = tf.reshape(diff_sort(tf_matrices, tf_input), (-1,))
with tf.Session() as s:
print(s.run((tf_output)))
>>> [-1.007 4.996 9.439 13.212 15.948 18.21 20.602 42. ]
This implementation was inspired by this tweet by @francoisfleuret:
Franรงois Fleuret @francoisfleuret Jun 14
Discussion with Ronan Collober reminded me that (max, +) is a semi-ring, and made me realize that the same is true for (softmax, +) where
softmax(a, b) = log(exp(a) + exp(b))
All this coolness at the heart of his paper
https://arxiv [dot] org/abs/1902.06022
Error analysis
The plot below shows the relative RMS (RMS error divided by the maximum range of the input vector) between the softmax sorted array and the ground truth sorted array, for vectors of length n=2 through n=512, with test values distributed randomly uniformly in ranges from [0, 2^-5] to [0, 2^10]. The main factor affecting precision is the numerical range. Small values will be corrupted, but values > ~300 will overflow (in float64). The dotted line is shown at 10% relative error.
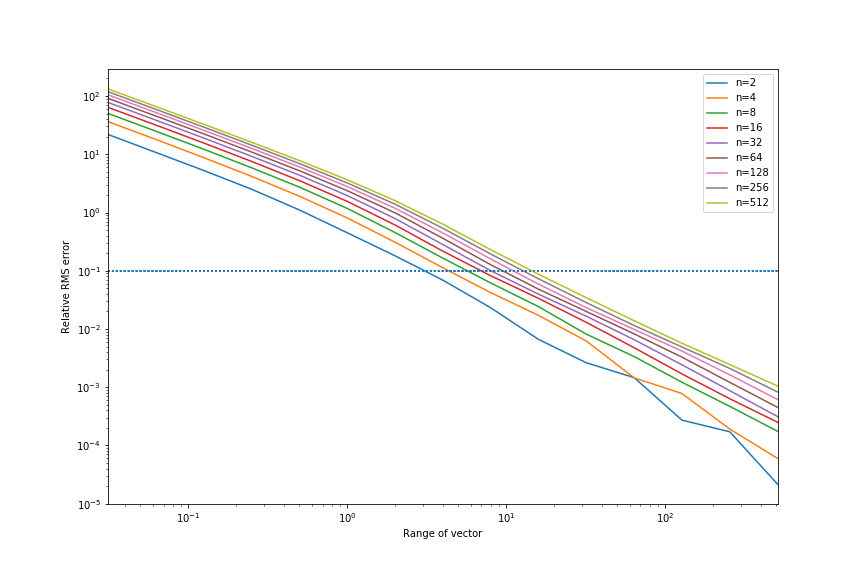
Softmax error curve.
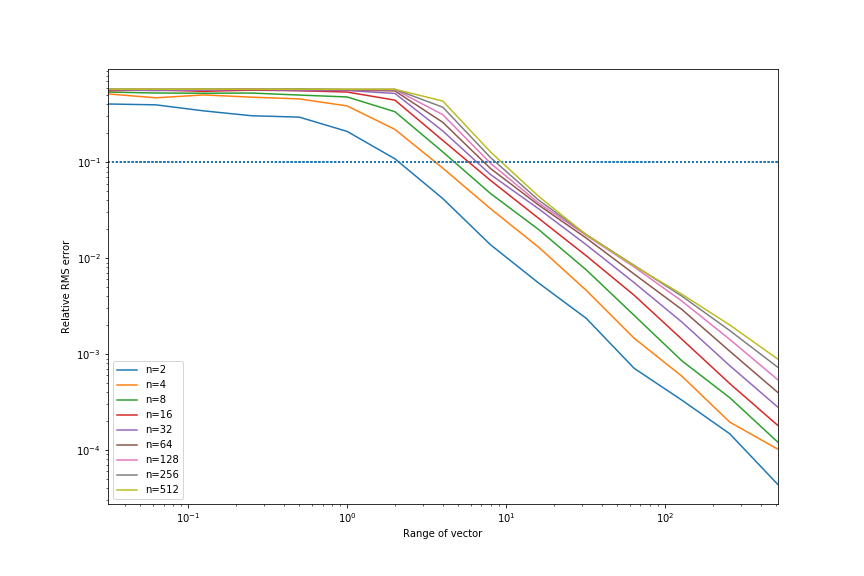
Smoothmax error curve.
There is also a function to pretty-print bitonic networks:
pretty_bitonic_network(8)
0 1 2 3 4 5 6 7
โญโโโฏ โ โ โ โ โ โ
โ โ โฐโโโฎ โ โ โ โ
โ โ โ โ โญโโโฏ โ โ
โ โ โ โ โ โ โฐโโโฎ
โญโโโโโโฏ โ โ โ โ โ
โ โญโโโโโโฏ โ โ โ โ
โ โ โ โ โฐโโโโโโฎ โ
โ โ โ โ โ โฐโโโโโโฎ
โญโโโฏ โ โ โ โ โ โ
โ โ โญโโโฏ โ โ โ โ
โ โ โ โ โฐโโโฎ โ โ
โ โ โ โ โ โ โฐโโโฎ
โญโโโโโโโโโโโโฏ โ โ โ
โ โญโโโโโโโโโโโโฏ โ โ
โ โ โญโโโโโโโโโโโโฏ โ
โ โ โ โญโโโโโโโโโโโโฏ
โญโโโโโโฏ โ โ โ โ โ
โ โญโโโโโโฏ โ โ โ โ
โ โ โ โ โญโโโโโโฏ โ
โ โ โ โ โ โญโโโโโโฏ
โญโโโฏ โ โ โ โ โ โ
โ โ โญโโโฏ โ โ โ โ
โ โ โ โ โญโโโฏ โ โ
โ โ โ โ โ โ โญโโโฏ