torchcde

Differentiable GPU-capable solvers for CDEs

This library provides differentiable GPU-capable solvers for controlled differential equations (CDEs). Backpropagation through the solver or via the adjoint method is supported; the latter allows for improved memory efficiency.

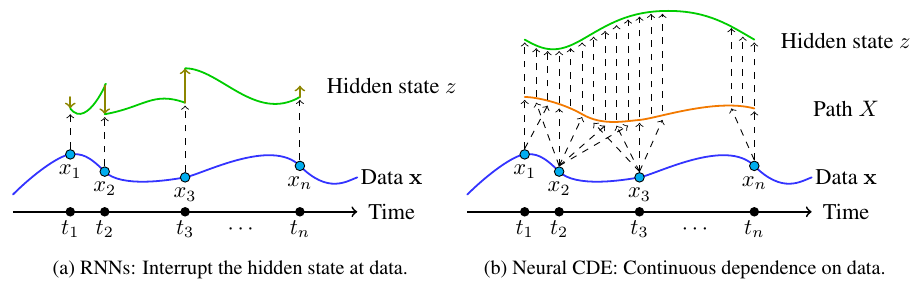
In particular this allows for building Neural Controlled Differential Equation models, which are state-of-the-art models for (arbitrarily irregular!) time series. Neural CDEs can be thought of as a "continuous time RNN".

Installation

pip install git+https://github.com/patrick-kidger/torchcde.git

Requires PyTorch >=1.7 and torchdiffeq >= 0.2.0.

Example

We encourage looking at time_series_classification.py, which demonstrates how to use the library to train a Neural CDE model to predict the chirality of a spiral.

Also see irregular_data.py, for demonstrations on how to handle variable-length inputs, irregular sampling, or missing data, all of which can be handled easily, without changing the model.

A short self contained example:

import torch
import torchcde

# Create some data
batch, length, input_channels = 1, 10, 2
hidden_channels = 3
t = torch.linspace(0, 1, length)
t_ = t.unsqueeze(0).unsqueeze(-1).expand(batch, length, 1)
x_ = torch.rand(batch, length, input_channels - 1)
x = torch.cat([t_, x_], dim=2)  # include time as a channel

# Interpolate it
coeffs = torchcde.natural_cubic_coeffs(x)
X = torchcde.NaturalCubicSpline(coeffs)

# Create the Neural CDE system
class F(torch.nn.Module):
    def __init__(self):
        super(F, self).__init__()
        self.linear = torch.nn.Linear(hidden_channels, 
                                      hidden_channels * input_channels)
    def forward(self, t, z):
        return self.linear(z).view(batch, hidden_channels, input_channels)

func = F()
z0 = torch.rand(batch, hidden_channels)

# Integrate it
torchcde.cdeint(X=X, func=func, z0=z0, t=X.interval)

Citation

If you found use this library useful, please consider citing

@article{kidger2020neuralcde,
    title={{N}eural {C}ontrolled {D}ifferential {E}quations for {I}rregular {T}ime {S}eries},
    author={Kidger, Patrick and Morrill, James and Foster, James and Lyons, Terry},
    journal={Advances in Neural Information Processing Systems},
    year={2020}
}

Documentation

The library consists of two main components: (1) integrators for solving controlled differential equations, and (2) ways of constructing controls from data.

Integrators

The library provides the cdeint function, which solves the system of controlled differential equations:

dz(t) = f(t, z(t))dX(t)     z(t_0) = z0

The goal is to find the response z driven by the control X. This can be re-written as the following differential equation:

dz/dt(t) = f(t, z)dX/dt(t)     z(t_0) = z0

where the right hand side describes a matrix-vector product between f(t, z) and dX/dt(t).

This is solved by

cdeint(X, func, z0, t, adjoint, **kwargs)

where letting ... denote an arbitrary number of batch dimensions:

• X is a torch.nn.Module with method derivative, such that X.derivative(t) is a Tensor of shape (..., input_channels),
• func is a torch.nn.Module, such that func(t, z) returns a Tensor of shape (..., hidden_channels, input_channels),
• z0 is a Tensor of shape (..., hidden_channels),
• t is a one-dimensional Tensor of times to output z at.
• adjoint is a boolean (defaulting to True).

Adjoint backpropagation (which is slower but more memory efficient) can be toggled with adjoint=True/False and any additional **kwargs are passed on to torchdiffeq.odeint[_adjoint], for example to specify the solver.

Constructing controls

A very common scenario is to construct the continuous controlX from discrete data (which may be irregularly sampled with missing values). To support this, we provide three main interpolation schemes:

• Natural cubic splines
• Linear interpolation
• Rectilinear interpolation

Note that if for some reason you already have a continuous control X then you won't need an interpolation scheme at all!

Natural cubic splines are usually the best choice, if your data isn't arriving continuously over time. Natural cubic splines aren't causal, so you need to have all your data up-front. (If you're a mathematician then we use 'causality' in the precise sense of 'measurable with respect to the natural filtration of the data'.) This is what was used in the original Neural CDE paper. If causality is a concern then one of the two linear interpolations should be used, see the Further Documentation below.

Just demonstrating natural cubic splines for now:

coeffs = natural_cubic_coeffs(x)

# coeffs is a torch.Tensor you can save, load,
# pass through Datasets and DataLoaders etc.

X = NaturalCubicSpline(coeffs)

where:

• x is a Tensor of shape (..., length, input_channels), where ... is some number of batch dimensions. Missing data should be represented as a NaN.

The interface provided by NaturalCubicSpline is:

• .interval, which gives the time interval the spline is defined over. (Often used as the t argument in cdeint.) This is determined implicitly from the length of the data, and so does not in general correspond to the time your data was actually observed at. (See the Further Documentation note on reparameterisation invariance.)
• .grid_points is all of the knots in the spline, so that for example X.evaluate(X.grid_points) will recover the original data.
• .evaluate(t), where t is an any-dimensional Tensor, to evaluate the spline at any (collection of) time(s).
• .derivative(t), where t is an any-dimensional Tensor, to evaluate the derivative of the spline at any (collection of) time(s).

Usually natural_cubic_coeffs should be computed as a preprocessing step, whilst NaturalCubicSpline should be called inside the forward pass of your model. See time_series_classification.py for a worked example.

Then call:

cdeint(X=X, func=... z0=..., t=X.interval)

Further documentation

The earlier documentation section should give everything you need to get up and running.

Here we discuss a few more advanced bits of functionality:

• The reparameterisation invariance property of CDEs.
• Other interpolation methods, and the differences between them.
• The use of fixed solvers. (They just work.)
• Stacking CDEs (i.e. controlling one by the output of another).
• Computing logsignatures for the log-ODE method.

Reparameterisation invariance

This is a classical fact about CDEs.

Let be differentiable and increasing, with and . Let , let , let , and let . Then substituting into a CDE (and just using the standard change of variables formula):

We see that also satisfies the neural CDE equation, just with as input instead of . In other words, using changes the speed at which we traverse the input , and correspondingly changes the speed at which we traverse the output -- and that's it! In particular the CDE itself doesn't need any adjusting.

This ends up being a really useful fact for writing neater software. We can handle things like messy data (e.g. variable length time series) just during data preprocessing, without it complicating the model code. In time_series_classification.py, the region we integrate over is given by X.interval as a standardised region to integrate over. In the example irregular_data.py, we use this to handle variable-length data.

Different interpolation methods

In brief:

• Do you need causality?
  • No: natural cubic splines.
  • Yes: Is your data multivariate with missing values?
    • No: linear interpolation
    • Yes: rectilinear interpolation.

In more detail:

• Natural cubic splines: the fastest approach.

These were a simple choice used in the original Neural CDE paper. They are non-causal, but are very smooth, which makes them easy to integrate and thus fast to use in the differential equation solvers. These are usually the best choice if you don't need causality.

coeffs = natural_cubic_coeffs(x)
X = NaturalCubicSpline(coeffs)
cdeint(X=X, ...)

• Linear interpolation: these are "kind-of" causal.

If your data has just irregular sampling (but not missing data) then these are suitable: at inference you can wait at each time point for the next data point to arrive, then interpolate towards the next data point when it arrives, and solve the CDE over that interval.

If there is missing data, however, then this isn't possible. (As some of the channels don't have observations you can interpolate to.) In this case use rectilinear interpolation, below.

Linear interpolation has kinks. If using adaptive solvers then it should be told about the kinks. (Rather than expensively finding them for itself -- slowing down to resolve the kink, and then speeding up again afterwards.) This is done with the jump_t option (provided by torchdiffeq):

coeffs = linear_interpolation_coeffs(x)
X = LinearInterpolation(coeffs)
cdeint(X=X, ...,
       method='dopri5',
       options=dict(jump_t=X.grid_points))

• Rectilinear interpolation: This is appropriate if there is missing data, and you need causality.

What is done is to linearly interpolate forward in time (keeping the observations constant), and the linearly interpolate the values (keeping the time constant). This is possible because time is a channel (and doesn't need to line up with the "time" used in the differential equation solver, as per the reparameterisation invariance of the previous section).

t = torch.linspace(0, 1, 10)
x = torch.rand(2, 10, 3)
t_ = t.unsqueeze(0).unsqueeze(-1).expand(2, 10, 1)
x = torch.cat([t_, x], dim=-1)
del t, t_  # won't need these again!
# `rectilinear` is the channel index corresponding to time
coeffs = linear_interpolation_coeffs(x, rectilinear=0)
X = LinearInterpolation(coeffs)
cdeint(X=X, ...,
       method='dopri5',
       options=dict(jump_t=X.grid_points))

As before we should inform the solver about kinks.

This can be a bit unintuitive at first. We suggest firing up matplotlib and plotting things to get a feel for what's going on. As a fun sidenote, using rectilinear interpolation makes neural CDEs generalise ODE-RNNs.

Fixed solvers

Solving CDEs (regardless of the choice of interpolation scheme in a Neural CDE) with fixed solvers like euler, midpoint, rk4 etc. is pretty much exactly the same as solving an ODE with a fixed solver. Just make sure to set the step_size option to something sensible; for example the smallest gap between times:

X = LinearInterpolation(coeffs)
step_size = (X.grid_points[1:] - X.grid_points[:-1]).min()
cdeint(
    X=X, t=X.interval, func=..., method='rk4',
    options=dict(step_size=step_size)
)

Stacking CDEs

You may wish to use the output of one CDE to control another. That is, to solve the coupled CDEs:

du(t) = g(t, u(t)dz(t)      u(t_0) = u0
dz(t) = f(t, z(t))dX(t)     z(t_0) = z0

There are two ways to do this. The first way is to put everything inside a single cdeint call, by solving the system

v = [u, z]
v0 = [u0, z0]
h(t, v) = [g(t, u)f(t, z), f(t, z)]

dv(t) = h(t, v(t))dX(t)      v(t_0) = v0

and using cdeint as normal. This is usually the best way to do it! It's simpler and usually faster. (But forces you to use the same solver for the whole system, for example.)

The second way is to have cdeint output z(t) at multiple times t, interpolate the discrete output into a continuous path, and then call cdeint again. This is probably less memory efficient, but allows for different choices of solver for each call to cdeint.

For example, this could be used to create multi-layer Neural CDEs, just like multi-layer RNNs. Although as of writing this, no-one seems to have tried this yet!

The log-ODE method

This is a way of reducing the length of data by using extra channels. (For example, this may help train Neural CDE models faster, as the extra channels can be parallelised, but extra length cannot.)

This is done by splitting the control X up into windows, and computing the logsignature of the control over each window. The logsignature is a transform known to extract the information that is most important to describing how X controls a CDE.

This is supported by the logsig_windows function, which takes in data, and produces a transformed path, that now exists in logsignature space:

batch, length, channels = 1, 100, 2
x = torch.rand(batch, length, channels)
depth, window = 3, 10.0
x = torchcde.logsig_windows(x, depth, window)
# use x as you would normally: interpolate, etc.

See the paper Neural Rough Differential Equations for Long Time Series for more information.

Note that this requires installing the Signatory package.