xiadz / Cmov
Projects that are alternatives of or similar to Cmov
Comparing the performance of Intel's cmov instruction with a conditional branch + mov pair.
Suppose you want to write the following code inside a performance critical loop:
if(cond) {
foo = bar;
}
where foo is a local variable (of some simple type, like int),
and bar is either
a local variable, or a simple memory location (such as A[i]).
Such a code is likely to be found for example in a
Kadane's algorithm
implementation.
There are two standard ways for an x86-64 compiler to translate
this conditional into Intel assembly, namely a cmov
instruction, or a conditional branch paired with a regular mov.
To make this example more concrete I will focus on this particular code:
int j;
int res = 0;
for(j = 0; j < n; ++j) {
if(A[j]) {
res = j;
}
}
GCC version 4.8.2 emits the following code for the if
at -O3 (gas' assembly notation):
movl (%rdi,%rcx,4), %r9d
testl %r9d, %r9d
cmovne %ecx, %eax
Clearly the compiler stores the location of A in %rdi,
the value of j in %rcx (%ecx), and res in %rax (%eax).
We may however ask it to forget about the cmov instruction by
using the following command line parameters in addition to -O3:
-fno-tree-loop-if-convert
-fno-tree-loop-if-convert-stores
-fno-if-conversion
-fno-if-conversion2.
Then we will obtain the following assembly:
movl (%rdi,%rcx,4), %r9d
testl %r9d, %r9d
je .L4
movl %ecx, %eax
.L4:
To make this example more interesting let's feed the compiler
with more data. GCC (and others probably too) implements
a mechanism allowing the programmer to specify that a condition
will likely/unlikely be true during the runtime. In our case
it would look like this (assuming that we are expecting
A[j] to be generally false):
int j;
int res = 0;
for(j = 0; j < n; ++j) {
if(__builtin_expect(A[j], 0)) {
res = j;
}
}
The corresponding GCC output:
movl (%rdi,%rcx,4), %r9d
testl %r9d, %r9d
jne .L20
.L14:
/* Other code */
.L20:
movl %ecx, %eax
jmp .L14
We are of course free to put 1 in the place of 0 whenever
we expect A[j] to be true most of the time:
int j;
int res = 0;
for(j = 0; j < n; ++j) {
if(__builtin_expect(A[j], 1)) {
res = j;
}
}
And the corresponding GCC output (note the speculative
movl execution!):
movl %eax, %r8d
movl (%rdi,%rcx,4), %r10d
movl %ecx, %eax
testl %r10d, %r10d
je .L29
.L24:
/* Other code */
.L29:
movl %r8d, %eax
jmp .L24
This way we obtain four versions of the program which I will call cmov, branch, branch_0 and branch_1. One might ask why there is no cmov_0 and no cmov_1, but it is due to the fact that in cmov's case the compiler ignored the likely/unlikely hints.
The point of this excercise is to measure their execution
speed, but this of course depends on the contents of
the A array. So let's fill it with random independent
identically distributed zeros and ones,
manipulating the probability of one (the probability
that the if's condition will be true).
Update 2018:
Thanks to AndreasPK for providing this data.
On an i7-6700k (Skylake) cmov is now faster under all circumstances:
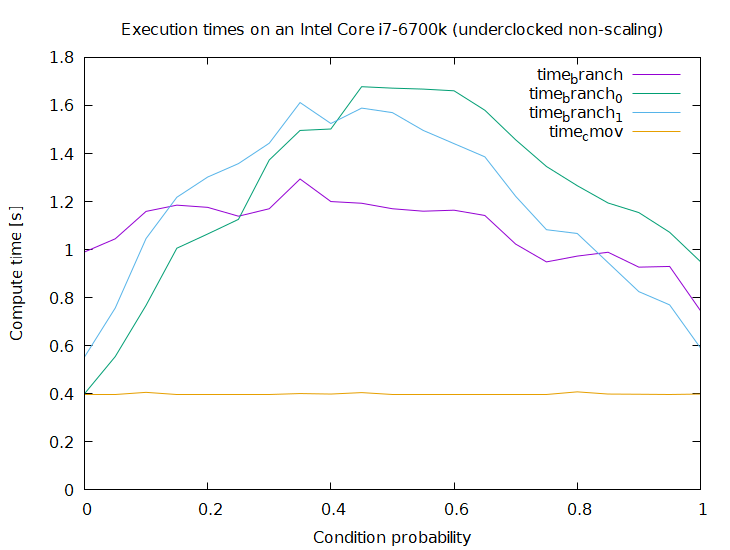
While the performance at the extremes looks the same cmov is still faster which becomes obvious when looking at the raw numbers:
0.000000;0.983000;0.412000;0.550000;0.411000
...
1.000000;0.747000;0.951000;0.591000;0.398000
branch_0 comes (very) close for probability zero but was still always slightly slower than cmov in 10 tests I ran.
Original Results
These are the results I obtained on my machine. It is
the execution time, so the lower the better:
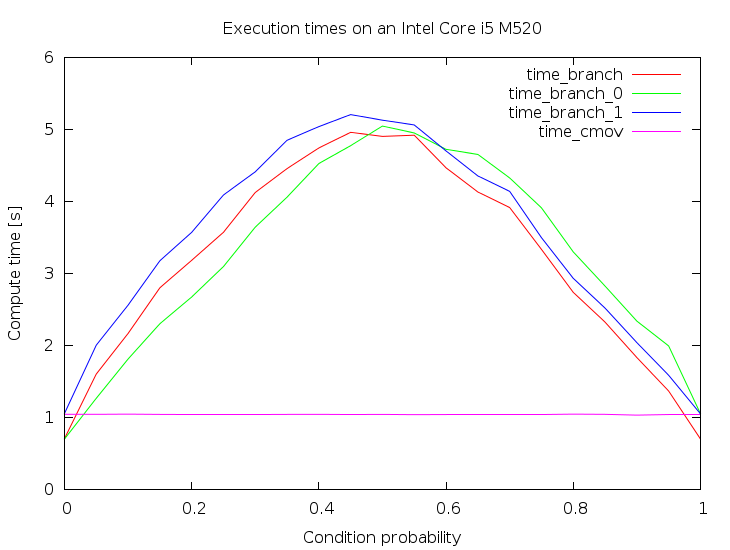
Three interesting facts can be read from this plot:
- The
cmovinstruction is generally faster. It is also immune to the probability - However the branch version is faster for stable, predictable conditions.
- The branch versions take approximately
p*(1-p)time to execute. The nice parabola-alike looks is approximately the variance of the distribution thatAwas sampled from.
The "visual proof" for the third fact:
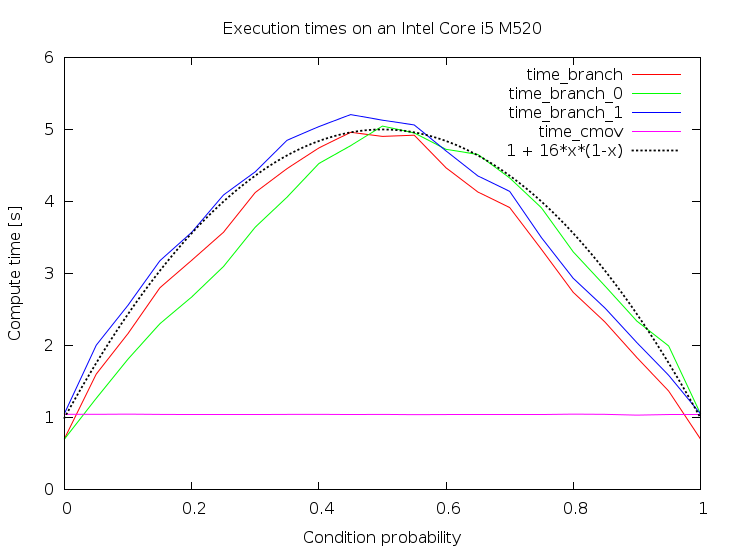
To conclude, GCC emits cmov by default, and it seems like
a reasonable choice, at least on my Intel Core i5. However,
as noted before, it is not the optimal solution for stable,
predictable conditions.
